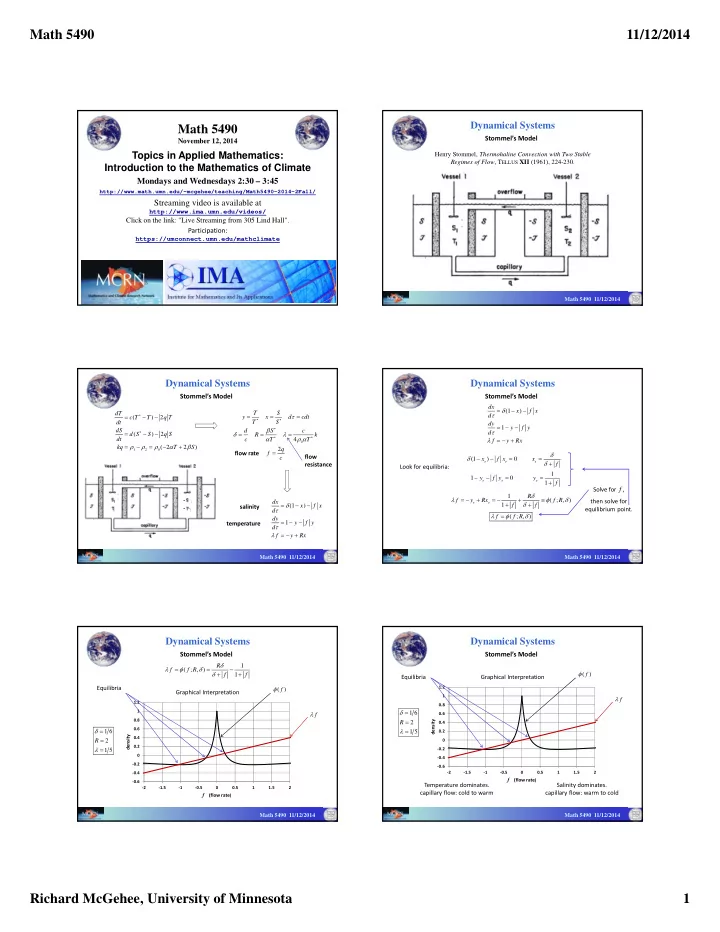
Math 5490 11/12/2014 Dynamical Systems Math 5490 Stommels Model - PDF document

Math 5490 11/12/2014 Dynamical Systems Math 5490 Stommel’s Model November 12, 2014 Topics in Applied Mathematics: Henry Stommel, Thermohaline Convection with Two Stable Regimes of Flow , T ELLUS XII (1961), 224-230. Introduction to the Mathematics of Climate Mondays and Wednesdays 2:30 – 3:45 http://www.math.umn.edu/~mcgehee/teaching/Math5490-2014-2Fall/ Streaming video is available at http://www.ima.umn.edu/videos/ Click on the link: "Live Streaming from 305 Lind Hall". Participation: https://umconnect.umn.edu/mathclimate Math 5490 11/12/2014 Dynamical Systems Dynamical Systems Stommel’s Model Stommel’s Model dx     (1 x ) f x T S dT          d c T ( T ) 2 q T y x d cdt   dt T S dy    1 y f y   dS d S c           d ( ) 2 d S S q S R k          dt c T 4 T f y Rx 0           ( 2 2 ) kq T S 2 q 1 2 0  flow rate f  flow      c (1 x ) f x 0 x   e e e resistance f Look for equilibria: 1     1 y f y 0 y  e e e 1 f Solve for f ,  1 R           ( ; , ) - f y Rx f R then solve for dx e e        (1 x ) f x 1 f f salinity -  equilibrium point. d     f ( ; , ) f R dy    temperature 1 y f y  d     f y Rx Math 5490 11/12/2014 Math 5490 11/12/2014 Dynamical Systems Dynamical Systems Stommel’s Model Stommel’s Model  R 1       f ( ; , ) f R     ( ) f f 1 f Graphical Interpretation Equilibria Equilibria  1.2 ( ) f Graphical Interpretation 1  f 1.2 0.8 1    1 6 0.6 f 0.8  R 2 density 0.4   0.6   1 6 1 5 0.2 density  0.4 R 2 0 0.2   ‐ 0.2 1 5 0 ‐ 0.4 ‐ 0.2 ‐ 0.6 ‐ 2 ‐ 1.5 ‐ 1 ‐ 0.5 0 0.5 1 1.5 2 ‐ 0.4 f (flow rate ) ‐ 0.6 Temperature dominates. Salinity dominates. ‐ 2 ‐ 1.5 ‐ 1 ‐ 0.5 0 0.5 1 1.5 2 capillary flow: cold to warm capillary flow: warm to cold f (flow rate ) Math 5490 11/12/2014 Math 5490 11/12/2014 Richard McGehee, University of Minnesota 1

Math 5490 11/12/2014 Dynamical Systems Dynamical Systems Stommel’s Model Stommel’s Model Equilibrium Conditions       (1 x ) f x 0 x Temperature e e e   Salinity dominates. f dominates. 1 capillary flow:     1 y f y 0 y capillary flow: e e e  1 f warm to cold cold to warm  1 R        f y Rx    e e 1 f f Solve for f ,   1 6 then solve for equilibrium point.  R 2          1 5            f 1 f f f R 1 f         2       f (1 ) f f ( R 1) (1 R ) f               3 f (1 ) f f f (1 R ) f ( R 1) 0 Stommel, T ELLUS XII (1961) Math 5490 11/12/2014 Math 5490 11/12/2014 Dynamical Systems Dynamical Systems Stommel’s Model Stommel’s Model Equilibrium Conditions: Solving for f  ( ) f Graphical Interpretation  3              f (1 ) f f f (1 R ) f ( R 1) 0 1.2      Parameters: 1 6 R 2 1 5 1  f           1 3 1 1 1 1 1 1 f (1 ) f f f (1 2 ) f (2 1) 0 0.8 5 5 6 5 6 6 6   1 6 0.6 3  7     1 f f f 1 f 2 f 1 0  5 30 30 3 6 R 2 density 0.4    Case 1: f 0 1 5 0.2     1 3 7 2 21 1 0 f f f 0 5 30 30 6 ‐ 0.2 f  Solve numerically. Only one positive root: 0.21909 ‐ 0.4  Case 2: f 0 ‐ 0.6 ‐ 2 ‐ 1.5 ‐ 1 ‐ 0.5 0 0.5 1 1.5 2 1 3  7 2  19  1  f f f 0 f (flow rate ) 5 30 30 6 f  -1.068 -0.307 0.219 Solve numerically. Two negative roots: -1.06791, -0.30703 Math 5490 11/12/2014 Math 5490 11/12/2014 Dynamical Systems Dynamical Systems Stommel’s Model Stommel’s Model f  0   1 6 Rest Points  R 2  1 1      1 5 x , y     Temperature e e f 1 6 f 1 f f  dominates. 0 c b capillary flow:  point : a f -1.06791: cold to warm 1 1     x 0.13500, y 0.48358   e e 1 6 -1.06791 1 -1.06791  point : b f -0.30703: a 1 1 f      0 x 0.35184, y 0.76510   e e 1 6 -1.06791 1 -1.06791   1 6 Salinity dominates.  point : c 0.21909:  f R 2 capillary flow:   1 1 1 5     x 0.43205, y 0.82 028 warm to cold   e e 1 6 -1.06791 1 -1.06791 Math 5490 11/12/2014 Math 5490 11/12/2014 Richard McGehee, University of Minnesota 2

Math 5490 11/12/2014 Dynamical Systems Dynamical Systems Stommel’s Model Stommel’s Model   1 6 Structure of Rest Points Rest Point c  R 2     f 0.21909 0, x 0.43205, y 0.82028        x (1 x ) f x e e 1 5     f y Rx     y 1 y f y Jacobian matrix Jacobian matrix     2 1 R 1        1 0.21909 0.43205 0.43205 f x x           6 f f   1 5 1 5 f f 1 R R 1                    f 0 : f y x , , f x x           x y  R y 1  2 1 x y           1 f y 0.82028 1 0.21909 0.82028                 1 5 1 5 f f 1 R f R f 1             f 0 : f y x , , y 1 f y              x y 4.70627 2.16025 x y      8.20284 2.88233  f  f  0 0       determinant 4.15521 0 R 1 R 1           f x x   f x x         stable trace 1.82394 0        spiral  R y 1   R y 1  discriminant 13.29410 0         1 f y 1 f y             Math 5490 11/12/2014 Math 5490 11/12/2014 Dynamical Systems Dynamical Systems Stommel’s Model Stommel’s Model f    0 1 6 Rest Point b  R 2        f 0.30703 0, x 0.35184, y 0.76510 1 5 e e Temperature f  dominates. 0 Jacobian matrix c b   capillary flow:   2 1 R 1  1          0.30703 0.35184 0.35184 f x x     6 cold to warm   1 5 1 5      stable spiral    R y 1  2 1          1 f y  0.76510 1 0.30703 0.76510          1 5 1 5 a    3.04476 1.75922   f   0    7.65095 5.13250   1 6 Salinity dominates.  R 2 capillary flow:    eigenvalue 7.60883 eigenvalue 0.28486   1 5 warm to cold saddle     0.61023 0.28604     eigenvector  eigenvector   0.79222   0.95822  Math 5490 11/12/2014 Math 5490 11/12/2014 Dynamical Systems Dynamical Systems Stommel’s Model Stommel’s Model f    0 1 6 Rest Point a  stable vector R 2       1 5 f -1.06791 0, x 0.13500, y 0.48358 e e f  0 Jacobian matrix c unstable vector b     2 1 R 1  1         -1.06791 0.13500 0.13500    f x x    6 1 5 1 5      stable spiral    R y 1  2 1         1 f y 0.48358 1 -1.06791 0.48358          1 5 1 5    a saddle 1 6   0.11541 -0.67500     R 2   0.48358 -4.48581   1 5     f  eigenvalue 0.76088 eigenvalue 3.60951 0 stable node     0.61023 0.17831     eigenvector  eigenvector   0.79222   0.98398  Math 5490 11/12/2014 Math 5490 11/12/2014 Richard McGehee, University of Minnesota 3