Linear, Binary SVM Classifiers COMPSCI 371D Machine Learning - PowerPoint PPT Presentation

Linear, Binary SVM Classifiers COMPSCI 371D — Machine Learning COMPSCI 371D — Machine Learning Linear, Binary SVM Classifiers 1 / 17

Outline 1 What Linear, Binary SVM Classifiers Do 2 Margin 3 Loss and Regularized Risk 4 Training an SVM is a Quadratic Program 5 The KKT Conditions and the Support Vectors COMPSCI 371D — Machine Learning Linear, Binary SVM Classifiers 2 / 17

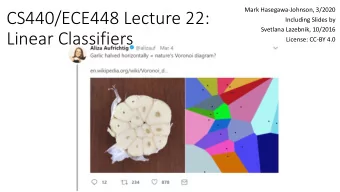
What Linear, Binary SVM Classifiers Do The Separable Case ? • Where to place the boundary? • The number of degrees of freedom grows with d COMPSCI 371D — Machine Learning Linear, Binary SVM Classifiers 3 / 17

What Linear, Binary SVM Classifiers Do SVMs Maximize the Smallest Margin • Placing the boundary as far as possible from the nearest samples improves generalization • Leave as much empty space around the boundary as possible • Only the points that barely make the margin matter • These are the support vectors • Initially, we don’t know which points will be support vectors COMPSCI 371D — Machine Learning Linear, Binary SVM Classifiers 4 / 17

What Linear, Binary SVM Classifiers Do The General Case • If the data is not linearly separable, there must be misclassified samples. These have a negative margin • Assign a penalty that increases when the smallest margin diminishes (penalize a small margin between classes), and grows with any negative margin (penalize misclassified samples) • Give different weights to the two penalties (cross-validation!) • Find the optimal compromise: minimum risk (total penalty) COMPSCI 371D — Machine Learning Linear, Binary SVM Classifiers 5 / 17

Margin Separating Hyperplane • X = R d and Y = {− 1 , 1 } (more convenient labels) • Hyperplane: n T x + c = 0 with � n � = 1 • Decision rule: ˆ y = h ( x ) = sign ( n T x + c ) • n points towards the ˆ y = 1 half-space • If y is the true label, decision is correct if � n T x + c ≥ 0 if y = 1 n T x + c ≤ 0 if y = − 1 • More compactly, decision is correct if y ( n T x + c ) ≥ 0 • SVMs want this inequality to hold with a margin COMPSCI 371D — Machine Learning Linear, Binary SVM Classifiers 6 / 17

Margin Margin • The margin of ( x , y ) is the n signed distance of x from ^ ^ = 1 y = − 1 y the boundary: Positive if x is on the correct side of the boundary, negative otherwise separating hyperplane def = y ( n T x + c ) µ v ( x , y ) µ ( x , 1) v 1 • v = ( n , c ) 1 • Margin of a training set T : def µ v ( T ) = min ( x , y ) ∈ T µ v ( x , y ) µ ( x , -1) v • Boundary separates T if µ v ( T ) > 0 1 COMPSCI 371D — Machine Learning Linear, Binary SVM Classifiers 7 / 17

Loss and Regularized Risk The Hinge Loss reference reference margin margin • Reference margin µ ∗ > 0 (unknown, to be determined) n ^ ^ = 1 • Hinge loss ℓ v ( x , y ) : y = − 1 y µ ∗ max { 0 , µ ∗ − µ v ( x , y ) } 1 • Training samples with separating hyperplane µ v ( x , y ) ≥ µ ∗ l ( x , 1) v are classified correctly 1 with a margin at least µ ∗ µ * µ ( x , 1) • Some loss incurred as soon as v µ v ( x , y ) < µ ∗ l ( x , -1) v 1 even if the sample is classified correctly µ ( x , -1) µ * v COMPSCI 371D — Machine Learning Linear, Binary SVM Classifiers 8 / 17

Loss and Regularized Risk The Training Risk � N • The training risk for SVMs is not just 1 n = 1 ℓ v ( x n , y n ) N • A regularization term is added to force µ ∗ to be large • Separating hyperplane is n T x + c = 0 • Let w T x + b = 0 with w = ω n , b = ω c 1 and ω = � w � = µ ∗ • ω is a reciprocal scaling factor if w is changed for a fixed b : Large margin, small ω • Make risk higher when ω is large (small margin): 2 � w � 2 + C def � N 1 L T ( w , b ) = n = 1 ℓ ( w , b ) ( x n , y n ) N µ ∗ max { 0 , µ ∗ − µ ( w , b ) ( x , y ) } 1 where ℓ ( w , b ) ( x , y ) = µ ∗ max { 0 , µ ∗ − y ( n T x + c ) } = max { 0 , 1 − y ( w T x + b ) } 1 = COMPSCI 371D — Machine Learning Linear, Binary SVM Classifiers 9 / 17

Loss and Regularized Risk Regularized Risk • ERM classifier: ( w ∗ , b ∗ ) = ERM T ( w , b ) = arg min ( w , b ) L T ( w , b ) def 2 � w � 2 + C � N 1 where L T ( w , b ) = n = 1 ℓ ( w , b ) ( x n , y n ) N def = max { 0 , 1 − y n ( w T x n + b ) } • ℓ ( w , b ) ( x n , y n ) • C determines a trade-off • Large C ⇒ � w � less important ⇒ larger ω ⇒ smaller margin ⇒ fewer samples within the margin • We buy a larger margin by accepting more samples inside it • C is a hyper-parameter: Cross-validation! COMPSCI 371D — Machine Learning Linear, Binary SVM Classifiers 10 / 17

Training an SVM is a Quadratic Program Rephrasing as Training a Quadratic Program 2 � w � 2 + C � N • ( w ∗ , b ∗ ) = arg min ( w , b ) 1 n = 1 ℓ n where N def = max { 0 , 1 − y n ( w T x n + b ) ℓ n = ℓ ( w , b ) ( ν n ) } = max { 0 , 1 − ν n } � �� � ν n • Not differentiable because of the max : Bummer! • Neat trick: • Introduce new slack variables ξ n = ℓ n • Note that ξ n = ℓ n is the same as ξ n = min ξ ≥ ℓ n ξ l ( ν ) ( w , b) ξ l n 1 ν 0 ν n 1 • We moved ℓ n from the target to a constraint COMPSCI 371D — Machine Learning Linear, Binary SVM Classifiers 11 / 17

Training an SVM is a Quadratic Program Rephrasing as Training a Quadratic Program • Changed from 2 � w � 2 + C � N ( w ∗ , b ∗ ) = arg min ( w , b ) 1 n = 1 ℓ n ( ν n ) N 2 � w � 2 + C � N 1 to ( w ∗ , b ∗ ) = arg min ( w , b ) n = 1 ξ n N where ξ n are new variables subject to constraints ξ n ≥ ℓ n ( ν n ) • Now the target is a quadratic function of w , b , ξ 1 , . . . , ξ N • However, constraints are not affine • No problem: ξ n ≥ ℓ is the same as ξ n ≥ 0 and ξ n ≥ 1 − ν • Two affine constraints instead of one nonlinear one 1 µ 0 1 COMPSCI 371D — Machine Learning Linear, Binary SVM Classifiers 12 / 17

Training an SVM is a Quadratic Program Quadratic Program Formulation • We achieve differentiability at the cost of adding N slack variables ξ n : 2 � w � 2 + C � N 1 • Old: min ( w , b ) n = 1 ℓ ( w , b ) ( x n , y n ) N def = max { 0 , 1 − y n ( w T x n + b ) } where ℓ ( w , b ) ( x n , y n ) • New: 2 � w � 2 + γ � N f ( w , ξ ) = 1 min w , b , ξ f ( w , ξ ) where n = 1 ξ n subject to the constraints y n ( w T x n + b ) − 1 + ξ n ≥ 0 ≥ 0 ξ n def C and with γ = N • We have our quadratic program! COMPSCI 371D — Machine Learning Linear, Binary SVM Classifiers 13 / 17

The KKT Conditions and the Support Vectors The KKT Conditions SVM Quadratic Program N f ( w , ξ ) = 1 2 � w � 2 + γ � w , b , ξ f ( w , ξ ) min where ξ n n = 1 subject to the constraints y n ( w T x n + b ) − 1 + ξ n ≥ 0 ≥ 0 ξ n KKT Conditions ( u = ( w , b , ξ ) ) ∇ f ( u ∗ ) = � α ∗ i ∇ c i ( u ∗ ) with α ∗ i ≥ 0 i ∈A ( u ∗ ) COMPSCI 371D — Machine Learning Linear, Binary SVM Classifiers 14 / 17

The KKT Conditions and the Support Vectors Differentiating Target and Constraints 2 � w � 2 + γ � N f = 1 n = 1 ξ n • Two types of constraints: c j = y j ( w T x j + b ) − 1 + ξ j ≥ 0 d k = ξ k ≥ 0 • Unknowns w , b , ξ n ∂ c j ∂ f ∂ d k = y j x j = w = 0 ∂ w ∂ w ∂ w ∂ c j ∂ f ∂ d k = y j = 0 = 0 ∂ b ∂ b ∂ b ∂ c j ∂ f ∂ d k = 1 = γ = 1 ∂ξ j ∂ξ k ∂ξ n COMPSCI 371D — Machine Learning Linear, Binary SVM Classifiers 15 / 17

The KKT Conditions and the Support Vectors KKT Conditions � w ∗ α ∗ = n y n x n n ∈A ( u ∗ ) � α ∗ 0 = n y n n ∈A ( u ∗ ) α ∗ n + β ∗ γ = n for n = 1 , . . . , N α ∗ j , β ∗ 0 ≤ k A ( u ∗ ) is the set of indices where the constraints c j ≥ 0 are active COMPSCI 371D — Machine Learning Linear, Binary SVM Classifiers 16 / 17

The KKT Conditions and the Support Vectors The Support Vectors w ∗ = � N n ∈A ( u ∗ ) α ∗ • The representer theorem : n y n x n • The separating-hyperplane parameter w is a linear combination of the active training data points x n • Misclassified and low-margin points are active ( α n > 0) • In the separable case, data points on the margin boundaries are active • Either way, these data points are called the support vectors COMPSCI 371D — Machine Learning Linear, Binary SVM Classifiers 17 / 17