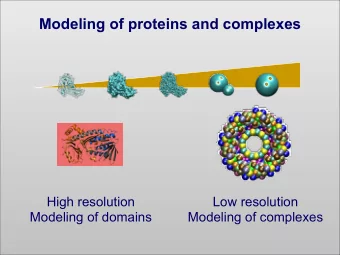
Cognitive Modeling Unseen Examples 2 Bayes Classifiers Lecture 14: - PowerPoint PPT Presentation

Decision Making as Classification Decision Making as Classification Bayes Classifiers Bayes Classifiers Naive Bayes Classifiers Naive Bayes Classifiers 1 Decision Making as Classification Decision Making Frequencies and Probabilities Cognitive Modeling Unseen Examples 2 Bayes Classifiers Lecture 14: Naive Bayes Classifiers Bayes’ Theorem Maximum A Posteriori Frank Keller Maximum Likelihood Properties School of Informatics 3 Naive Bayes Classifiers University of Edinburgh keller@inf.ed.ac.uk Parameter Estimation Properties February 19, 2006 Application to Decision Making Sparse Data Reading: Mitchell (1997: Ch. 6). Frank Keller Cognitive Modeling 1 Frank Keller Cognitive Modeling 2 Decision Making as Classification Decision Making Decision Making as Classification Decision Making Bayes Classifiers Frequencies and Probabilities Bayes Classifiers Frequencies and Probabilities Naive Bayes Classifiers Unseen Examples Naive Bayes Classifiers Unseen Examples Decision Making A Sample Data Set Bayes’ Theorem can be used to devised a general model of decision Sample data set (the medical diagnosis data from the last lecture): making: regard decision making as classification: given a set of symptom 1 symptom 2 disease attributes (the data) choose a target class (the decision); diarrhea fever mesiopathy decisions are based on frequency distributions in the diarrhea vomiting mesiopathy environment; paralysis headache mesiopathy paralysis vomiting ritengitis distributions can be updated incrementally as more data becomes available (model learns from experience). paralysis vomiting ritengitis General form of this model Bayes classifier. With certain simplifying assumptions: Naive Bayes classifier. Frank Keller Cognitive Modeling 3 Frank Keller Cognitive Modeling 4

Decision Making as Classification Decision Making Decision Making as Classification Decision Making Bayes Classifiers Frequencies and Probabilities Bayes Classifiers Frequencies and Probabilities Naive Bayes Classifiers Unseen Examples Naive Bayes Classifiers Unseen Examples Frequencies and Probabilities Classifying an Unseen Example Now assume that we have to classify the following new instance: symptom 1 symptom 2 disease mes rite mes rite mes rite symptom 1 symptom 2 disease diarrhea 2 0 fever 1 0 3 2 paralysis vomiting ? paralysis 1 2 headache 1 0 vomiting 1 2 Key idea: compute a probability for each target class based on the probability distribution in the training data. First take into account the probability of each attribute. Treat all symptom 1 symptom 2 disease attributes equally important, i.e., multiply the probabilities: mes rite mes rite mes rite diarrhea 2/3 0/2 fever 1/3 0/2 3/5 2/5 P (mesiopathy) = 1 / 3 · 1 / 3 = 1 / 9 paralysis 1/3 2/2 headache 1/3 0/2 P (ritengitis) = 2 / 2 · 2 / 2 = 1 vomiting 1/3 2/2 Frank Keller Cognitive Modeling 5 Frank Keller Cognitive Modeling 6 Bayes’ Theorem Decision Making as Classification Decision Making Decision Making as Classification Maximum A Posteriori Bayes Classifiers Frequencies and Probabilities Bayes Classifiers Maximum Likelihood Naive Bayes Classifiers Unseen Examples Naive Bayes Classifiers Properties Classifying an Unseen Example Bayes’ Theorem This procedure is based on Bayes’ Theorem: Bayes’ Theorem Now take into account the overall probability of a given class. Given a hypothesis h and data D which bears on the hypothesis: Multiply it with the probabilities of the attributes: P ( h | D ) = P ( D | h ) P ( h ) P (mesiopathy) = 1 / 9 · 3 / 5 = 0 . 067 P ( D ) P (ritengitis) = 1 · 2 / 5 = 0 . 4 P ( h ): independent probability of h : prior probability Now choose the class so that it maximizes this probability. This P ( D ): independent probability of D means that the new instance will be classified as ritengitis. P ( D | h ): conditional probability of D given h : likelihood P ( h | D ): conditional probability of h given D : posterior probability Frank Keller Cognitive Modeling 7 Frank Keller Cognitive Modeling 8

Bayes’ Theorem Bayes’ Theorem Decision Making as Classification Decision Making as Classification Maximum A Posteriori Maximum A Posteriori Bayes Classifiers Bayes Classifiers Maximum Likelihood Maximum Likelihood Naive Bayes Classifiers Naive Bayes Classifiers Properties Properties Maximum A Posteriori Maximum Likelihood Based on Bayes’ Theorem, we can compute the maximum a Now assume that all hypotheses are equally probable a priori, i.e., posteriori (MAP) hypothesis for the data: P ( h i ) = P ( h j ) for all h i , h j ∈ H . (1) = argmax P ( h | D ) h MAP This is called assuming a uniform prior. It simplifies computing the h ∈ H posterior: P ( D | h ) P ( h ) = argmax P ( D ) (2) h ML = argmax P ( D | h ) h ∈ H = argmax P ( D | h ) P ( h ) h ∈ H h ∈ H This hypothesis is called the maximum likelihood hypothesis. H : set of all hypotheses. It can be regarded as a model of decision making with base rate Note that we can drop P ( D ) as the probability of the data is neglect. constant (and independent of the hypothesis). Frank Keller Cognitive Modeling 9 Frank Keller Cognitive Modeling 10 Bayes’ Theorem Parameter Estimation Decision Making as Classification Decision Making as Classification Maximum A Posteriori Properties Bayes Classifiers Bayes Classifiers Maximum Likelihood Application to Decision Making Naive Bayes Classifiers Naive Bayes Classifiers Properties Sparse Data Properties Naive Bayes Classifiers Assumption: training set consists of instances described as conjunctions of attributes values. The target classification based on Bayes classifiers have the following desirable properties: finite set of classes V . Incrementality: with each training example, the prior and the The task of the learner is to predict the correct class for a new likelihood can be updated dynamically: flexible and robust to instance � a 1 , a 2 , . . . , a n � . errors. Key idea: assign most probable class v MAP using Bayes’ Theorem. Combines prior knowledge and observed data: prior probability of a hypothesis multiplied with probability of the hypothesis (3) v MAP = argmax P ( v j | a 1 , a 2 , . . . , a n ) given the training data. v j ∈ V P ( a 1 , a 2 , . . . , a n | v j ) P ( v j ) Probabilistic hypotheses: outputs not only a classification, but = argmax P ( a 1 , a 2 , . . . , a n ) a probability distribution over all classes. v j ∈ V = argmax P ( a 1 , a 2 , . . . , a n | v j ) P ( v j ) v j ∈ V Frank Keller Cognitive Modeling 11 Frank Keller Cognitive Modeling 12

Parameter Estimation Parameter Estimation Decision Making as Classification Decision Making as Classification Properties Properties Bayes Classifiers Bayes Classifiers Application to Decision Making Application to Decision Making Naive Bayes Classifiers Naive Bayes Classifiers Sparse Data Sparse Data Parameter Estimation Properties Estimating P ( v j ) is simple: compute the relative frequency of each target class in the training set. Estimating P ( a i | v j ) instead of P ( a 1 , a 2 , . . . , a n | v j ) greatly Estimating P ( a 1 , a 2 , . . . , a n | v j ) is difficult: typically not enough reduces the number of parameters (and data sparseness). instances for each attribute combination in the training set: sparse data problem. The learning step in Naive Bayes consists of estimating P ( a i | v j ) and P ( v j ) based on the frequencies in the training Independence assumption: attribute values are conditionally data. independent given the target value: naive Bayes. An unseen instance is classified by computing the class that � (4) P ( a 1 , a 2 , . . . , a n | v j ) = P ( a i | v j ) maximizes the posterior. i When conditional independence is satisfied, Naive Bayes Hence we get the following classifier: corresponds to MAP classification. � (5) v NB = argmax P ( v j ) P ( a i | v j ) v j ∈ V i Frank Keller Cognitive Modeling 13 Frank Keller Cognitive Modeling 14 Parameter Estimation Parameter Estimation Decision Making as Classification Decision Making as Classification Properties Properties Bayes Classifiers Bayes Classifiers Application to Decision Making Application to Decision Making Naive Bayes Classifiers Naive Bayes Classifiers Sparse Data Sparse Data Application to Decision Making Application to Decision Making Compute conditionals (examples): Apply Naive Bayes to our medical data. The hypothesis space is V = { mesiopathy , ritengitis } . Classify the following instance: P (sym1 = paralysis | disease = mes) = 1 / 3 P (sym1 = paralysis | disease = rite) = 2 / 2 symptom 1 symptom 2 disease paralysis vomiting ? Then compute the best class: P (mes) P (sym1 = paralysis | mes) P (sym2 = vomiting | disease = mes) � = 3 / 5 · 1 / 3 · 1 / 3 = 0 . 067 v NB = argmax P ( v j ) P ( a i | v j ) v j ∈{ mes , rite } P (rite) P (sym1 = paralysis | rite) P (sym2 = vomiting | disease = rite) i = argmax P ( v j ) P (sym1 = para | v j ) P (sym2 = vomit | v j ) = 2 / 5 · 2 / 2 · 2 / 2 = 0 . 4 v j ∈{ mes , rite } Now classify the unseen instance: Compute priors: = argmax P ( v j ) P (paralysis | v j ) P (vomiting | v j ) v NB v j ∈{ mes , rite } P (disease = mes) = 3 / 5 P (disease = rite) = 2 / 5 = ritengitis Frank Keller Cognitive Modeling 15 Frank Keller Cognitive Modeling 16