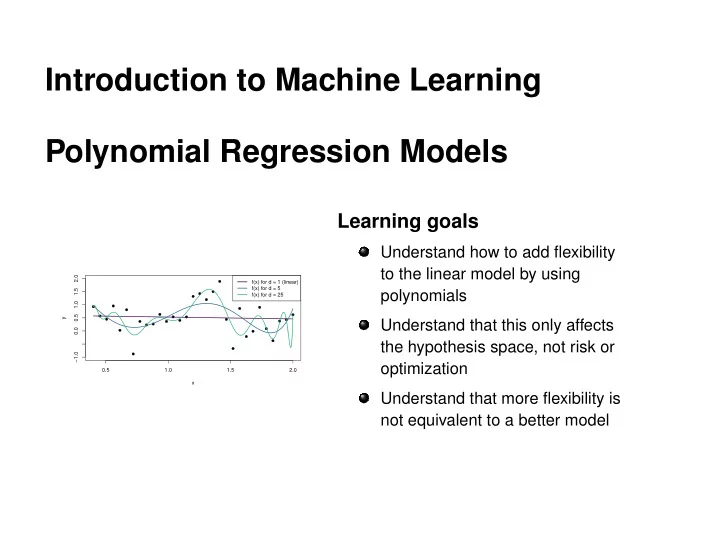

Introduction to Machine Learning Polynomial Regression Models Learning goals Understand how to add flexibility to the linear model by using 2.0 f(x) for d = 1 (linear) f(x) for d = 5 1.5 polynomials f(x) for d = 25 1.0 0.5 y Understand that this only affects 0.0 the hypothesis space, not risk or −1.0 optimization 0.5 1.0 1.5 2.0 x Understand that more flexibility is not equivalent to a better model
REGRESSION: POLYNOMIALS We can make linear regression models much more flexible by using polynomials x d j – or any other derived features like sin( x j ) or ( x j · x k ) – as additional features. The optimization and risk of the learner remain the same. Only the hypothesis space of the learner changes: instead of linear functions x ( i ) | θ � � = θ 0 + θ 1 x ( i ) 1 + θ 2 x ( i ) 2 + . . . f of only the original features, it now includes linear functions of the derived features as well, e.g. d d � k � k � x ( i ) | θ � � � x ( i ) x ( i ) � � f = θ 0 + θ 1 k + θ 2 k + . . . 1 2 k = 1 k = 1 � c Introduction to Machine Learning – 1 / 7
REGRESSION: POLYNOMIALS Polynomial regression example 2.0 1.5 1.0 0.5 y 0.0 −1.0 0.5 1.0 1.5 2.0 x � c Introduction to Machine Learning – 2 / 7
REGRESSION: POLYNOMIALS Polynomial regression example Models of different complexity , i.e., of different polynomial order d , are fitted to the data: 2.0 f(x) for d = 1 (linear) f(x) for d = 5 1.5 f(x) for d = 25 1.0 0.5 y 0.0 −1.0 0.5 1.0 1.5 2.0 x � c Introduction to Machine Learning – 3 / 7
REGRESSION: POLYNOMIALS Polynomial regression example Models of different complexity , i.e., of different polynomial order d , are fitted to the data: 2.0 f(x) for d = 1 (linear) f(x) for d = 5 1.5 f(x) for d = 25 1.0 0.5 y 0.0 −1.0 0.5 1.0 1.5 2.0 x � c Introduction to Machine Learning – 4 / 7
REGRESSION: POLYNOMIALS Polynomial regression example Models of different complexity , i.e., of different polynomial order d , are fitted to the data: 2.0 f(x) for d = 1 (linear) f(x) for d = 5 1.5 f(x) for d = 25 1.0 0.5 y 0.0 −1.0 0.5 1.0 1.5 2.0 x � c Introduction to Machine Learning – 5 / 7
REGRESSION: POLYNOMIALS The higher d is, the more capacity the learner has to learn complicated functions of x , but this also increases the danger of overfitting : The model space H contains so many complex functions that we are able to find one that approximates the training data arbitrarily well. However, predictions on new data are not as successful because our model has learnt spurious “wiggles” from the random noise in the training data (much, much more on this later). � c Introduction to Machine Learning – 6 / 7
REGRESSION: POLYNOMIALS Training Data 2.0 1.0 y 0.0 −1.0 0.5 1.0 1.5 2.0 x Test Data 2.0 1.0 y 0.0 −1.0 0.5 1.0 1.5 2.0 x � c Introduction to Machine Learning – 7 / 7
Recommend
More recommend