+ = hypotenuse CB 2 2 2 a b c opposite side AB = = = - PDF document

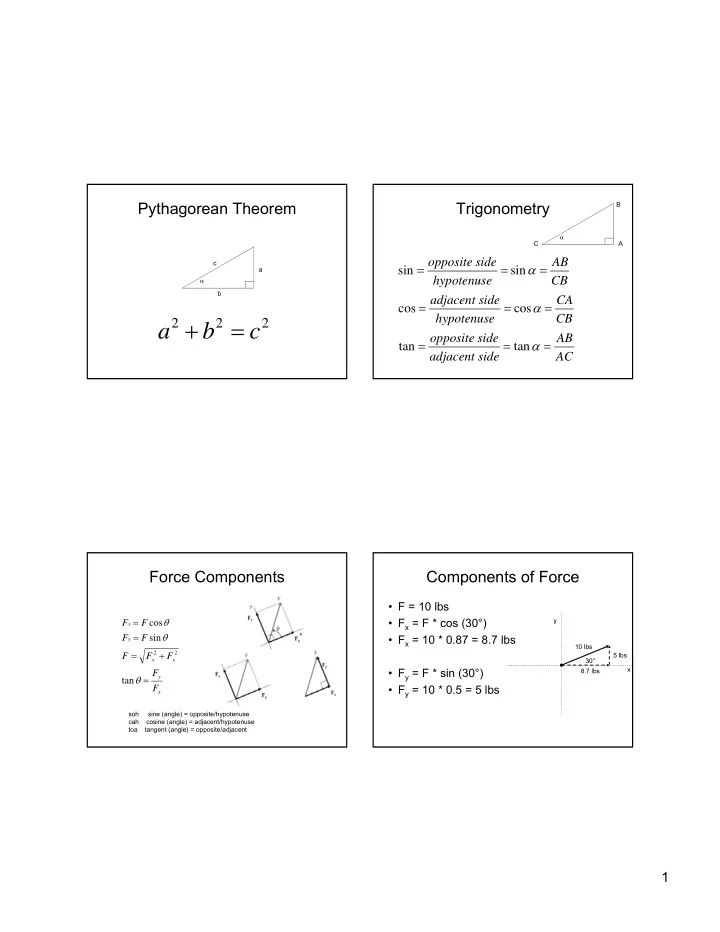
Pythagorean Theorem Trigonometry B α C A opposite side AB c = = α = sin sin a α hypotenuse CB b adjacent side CA = = α = cos cos + = hypotenuse CB 2 2 2 a b c opposite side AB = = α = tan tan adjacent side AC Force Components Components of Force • F = 10 lbs = θ • F x = F * cos (30°) y F F cos x = θ F F sin • F x = 10 * 0.87 = 8.7 lbs y 10 lbs = + 2 2 5 lbs F F F x y 30° x • F y = F * sin (30°) 8.7 lbs F θ = y tan • F y = 10 * 0.5 = 5 lbs F x soh sine (angle) = opposite/hypotenuse cah cosine (angle) = adjacent/hypotenuse toa tangent (angle) = opposite/adjacent 1

Components of Force How can we tell if forces are Similar Triangles balanced? • Find F x Find F y • Hypotenuse • The x and y components cancel y 20 lbs – Use pythagorean theorem – √ (3 2 +4 2 ) = 5 4 3 5 4 5 = = 3 F 20 F 20 y x x = = 4 * 20 5 * F 3 * 20 5 * F y x 5 * F * * 4 * 20 3 20 5 F = = y x 5 5 5 5 = = F 16 lbs F 12 lbs y x What is the balancing force? Translational Equilibrium • 10 lb force y 20 lbs • In order to be in translational equilibrium, the – F x = 10 * cos (30°) = -8.7 lbs 10 lbs total forces of the object must be zero. – F y = 10 * sin (30°) = 5 lbs 7 • Set the horizontal and vertical components of • 20 lb force 3 30° the forces to zero. – F x = 3*20/7.6 = 8 lbs x 88° – F y = 7*20/7.6= 18.4 lbs ∑ ∑ = = • Combine components F 0 F 0 – X: -8.7 + 8 = 0.7 lbs x y 23 lbs – Y: 5 + 18.4 = 23.4 lbs • Negative of these components represent balancing force – X = -0.7 lbs, y = -23.4 lbs – Resultant = √ (.7 2 + 23.4 2 ) = 23.4 lbs – Angle: tan-1(-23.4/-0.7) = 88° in third quadrant 2

Rotational Equilibrium Pole Vaulter Torque or Moment • In order to be in rotational equilibrium, the •Find the forces F L and F R . total torques acting on an object must be zero. ∑ ∑ τ = = F L 0 or M 0 pivot τ = ⋅ = ⋅ F d or M F d c.g. 2 ft. F G = 5 lbs F R 6 ft. The pole vaulter is holding pole so that it does not rotate and does not move. It is in equilibrium. Pole vaulter – con’t Pole vaulter – con’t τ = τ + τ = + + Rotation = 0 F F F F Translation = 0 net L G τ = τ + τ net L R G = + + = ⋅ + ⋅ − F F F F = + − 0 2 ft F 6 ft 5 lb 0 15 lbs F 5 lbs net L G net L R G L R τ = + = = = − F 0 r F r F F 10 lbs F 15 lbs net net L L G G R L τ = F L =15 lbs 0 net pivot c.g. 2 ft. F G = 5 lbs F R =10 lbs 6 ft. 3

Think – Pair - Share Answer • Pressure F = P • What exerts more pressure (in pounds per square inch) A when walking: a 100 lb woman in high heels or a 6,000 lb elephant in bare feet? • Woman’s heels • [At the moment when only the heel rests on the ground.] 100 lbs lbs = = = P 1600 1600 psi • Stiletto heels have an area of about 1/16 of a square 1 2 2 in in inch. 16 • Elephants, unlike humans, walk with two feet on the • Elephant’s feet ground at a time. 6000 lbs • Each foot is about 40 square inches. = = P 75 psi ⋅ 2 2 40 in • The heels exert more pressure! Equations Stress and Strain – example 1 Stress = ⋅ = • How far can you stretch a 20 ft steel cable before Stress E Strain E Strain it snaps? • E for steel is 2*10 11 N/m 2 Δ L Stress Stress • Ultimate tensile strength for steel is 5.2*10 8 N/m 2 = = = Strain E E Δ L L Strain Stress Stress Stress * L = = = E Δ Δ L Strain L L L L * Stress Δ = L • E is the modulus of elasticity E ⋅ 8 2 20 ft * 5 . 2 10 N m • Units of pressure (N/m 2 or psi) Δ = = = L 0 . 05 ft 0 . 6 inches ⋅ 11 2 2 10 N m 4

Middle Third Rule • Must stay within the “middle third” of the block to prevent the opposite side from going into tension – this is the important MIDDLE THIRD RULE. • Why is it important? Cables – Because bricks/stone/etc are much stronger in compression than in tension; need to keep them in compression or they can break! • To get around this problem – reinforce concrete with a steel bar – the steel can take the tension when the concrete can’t. • We’ll go over this in more detail in Chapter 8. Principal Elements for practical Vertical Supports or Towers suspension systems • Vertical supports or towers • Provide essential reactions that keep the cable system above the ground • Main cables • May be simple vertical or sloping piers or • Anchorages masts, diagonal struts, or a wall. • Stabilizers • Ideally, the axes of the supports should bisect the angle between the cables that pass over them 5

Main Cables Anchorages • Primary tensile elements • Because the cables are not vertical only, horizontal force resistance is required. • Carry roof with a minimum of material • In suspension bridges, the massive • Steel used in cable structures has concrete abutments provide the horizontal breaking stresses that exceed 200,000 psi reaction force Cables with a Single Concentrated Stabilizers Load l = 24’ h = 3’ • Lightweight roof or bridge systems are l susceptible to pronounced undulation or T y T T y T fluttering when acted upon by wind forces. A B h T x T x • Cables resist load through tension. 12’ C ( ) ( ) • The destructive force is vibration or flutter + = 2 2 3’ 12 ' 3 ' 12 . 4 ' W T = T y x [ ] 3 12 ∑ = F 0 y − = ⎛ ⎞ 2 T W 0 12 12 W = = = ⎜ ⎟ y T T 2 W x y ⎝ ⎠ 3 3 2 W = T y 2 6