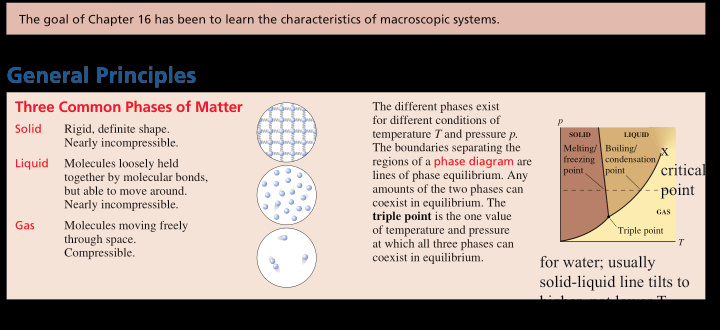



The goal of Chapter 16 has been to learn the characteristics of macroscopic systems. General Principles Three Common Phases of Matter The different phases exist for different conditions of p Solid Rigid, definite shape. temperature T and pressure p. SOLID LIQUID Nearly incompressible. x The boundaries separating the Melting/ Boiling/ freezing condensation regions of a phase diagram are Liquid Molecules loosely held critical point point lines of phase equilibrium. Any together by molecular bonds, point amounts of the two phases can but able to move around. coexist in equilibrium. The Nearly incompressible. GAS triple point is the one value Gas Molecules moving freely of temperature and pressure Triple point through space. at which all three phases can T Compressible. coexist in equilibrium. for water; usually solid-liquid line tilts to higher, not lower T Important Concepts M - 1 , T K 3 K K
A = # protons + # neutrons M mol = A gm Important Concepts Ideal-Gas Model Counting atoms and moles A macroscopic sample of matter consists of N atoms (or • Atoms and molecules are small, hard molecules), each of mass m (the atomic or molecular mass ): spheres that travel freely through space except for occasional collisions with N = M each other or the walls. m • The model is valid when the density is low and the Volume V Alternatively, we can state that temperature well above the condensation point. the sample consists of n moles: Mass M n = N N A or M Ideal-Gas Law M mol where N A = 6.02 * 10 23 mol - 1 is Avogadro’s number. The state variables of an ideal gas are related by the ideal-gas law The molar mass M mol , in kg/mol, is the numerical value of the pV = nRT or pV = Nk B T atomic or molecular mass in u divided by 1000. The atomic or where R = 8.31 J/mol K is the universal gas constant and molecular mass, in atomic mass units u, is well approximated k B = 1.38 * 10 - 23 J/K is Boltzmann’s constant. p, V, and T must by the atomic mass number A. The atomic mass unit is be in SI units of Pa, m 3 , and K. R = N A k B 1 u = 1.66 * 10 - 27 kg For a gas in a sealed container, with constant n : The number density of the sample is N p 2 V 2 = p 1 V 1 V . T 2 T 1 N A u = 1 gm K K
Applications Temperature scales Three basic gas processes pV diagram T F = 9 p 1. Isochoric, or constant volume T C + 32 � T K = T C + 273 2 5 2. Isobaric, or constant pressure 1 3 The Kelvin temperature scale is based on: • Absolute zero at T 0 = 0 K 3. Isothermal, or constant temperature V • The triple point of water at T 3 = 273.16 K
The goal of Chapter 17 has been to develop and apply the first law of thermodynamics. General Principles First Law of Thermodynamics Energy = Q - W by � E th = W + Q Thermal energy E th Microscopic energy of moving molecules on and stretched molecular bonds. � E th depends on the initial/final The first law is a general Work on Work by states but is independent of the process. statement of energy W � 0 W � 0 System conservation. Work W Energy transferred to the system by forces in a E th Work W and heat Q depend mechanical interaction. Q � 0 Q � 0 on the process by which the Heat in Heat out system is changed. Heat Q Energy transferred to the system via atomic-level collisions when there is a temperature difference. A thermal The change in the system depends only on the total energy interaction. exchanged W + Q , not on the process. L e) T 0. T = = = T 0 4 0 / T 0 T 0 / T V T 0 V ) 0 g 0 0 T T
Important Concepts p i The work done on a gas is The heat of transformation L is the energy needed to cause 1 kg of substance to undergo a phase change W = - 3 V f p dV Q = { ML V i f The specific heat c of a substance is the energy needed to raise = - (area under the pV curve) V the temperature of 1 kg by 1 K: W by = + area under pV curve Q = Mc � T The molar specific heat C is the energy needed to raise the An adiabatic process is one for p temperature of 1 mol by 1 K: which Q = 0. Gases move along an Adiabat adiabat for which pV g = constant, Q = nC � T where g = C P / C V is the specific heat Isotherms The molar specific heat of gases depends on the process by ratio. An adiabatic process changes which the temperature is changed: the temperature of the gas without C V = molar specific heat at constant volume heating it. V C P = C V + R = molar specific heat at constant pressure Heat is transferred by conduction, convection, radiation, and Calorimetry When two or more systems interact thermally, they evaporation. come to a common final temperature determined by Conduction: Q / � t = ( kA / L ) � T Q net = Q 1 + Q 2 + g = 0 Radiation: Q / � t = e s AT 4 0 / T 0 T 0 / T V T 0 V ) 0 g 0 0 T T
or TV γ -1 = Q - W by =W on = -W by S ummary of Basic Gas Processes Process Definition Stays constant Work Heat Isochoric � V = 0 V and p / T W = 0 Q = nC V � T Isobaric � p = 0 p and V / T W = - p � V Q = nC P � T � T = 0 � E th = 0 Isothermal T and pV W = - nRT ln ( V f / V i ) pV g Adiabatic Q = 0 W = � E th Q = 0 All gas processes First law � E th = W + Q = nC V � T Ideal-gas law pV = nRT
The goal of Chapter 18 has been to understand a macroscopic system in terms of the microscopic behavior of its molecules. General Principles The micro/macro connection relates the macroscopic properties of a system to the motion and collisions of its atoms and molecules. The Equipartition Theorem The Second Law of Thermodynamics Tells us how collisions distribute the energy in the system. Tells us how collisions move a system toward equilibrium. The energy stored in each mode of the system (each degree The entropy of an isolated system can only increase or, in of freedom ) is 1 2 Nk B T or, in terms of moles, 1 2 nRT . equilibrium, stay the same. • Order turns into disorder and randomness. • Systems run down. • Heat energy is transferred spontaneously from a hotter to a colder system, never from colder to hotter. al T , . T . R l
Important Concepts λ ~ ( N / V ) -1 r -2 Pressure is due to the force of the The thermal energy of a system is molecules colliding with the walls: E th = translational kinetic energy + rotational p = 1 N 2 = 2 N kinetic energy + vibrational energy mv rms P avg 3 V 3 V E th = 3 2 Nk B T = 3 • Monatomic gas 2 nRT at moderate T E th = 5 2 Nk B T = 5 • Diatomic gas 2 nRT The average translational kinetic energy of a molecule is • Elemental solid E th = 3 Nk B T = 3 nRT P avg = 3 2 2 k B T . The temperature of the gas T = 3 k B P avg measures the average translational kinetic energy. Heat is energy transferred via collisions from more-energetic molecules on one side to less- energetic molecules on the other. Entropy measures the probability that Equilibrium is reached when a macroscopic state will occur or, ( P 1 ) avg = ( P 2 ) avg , which implies equivalently, the amount of disorder T 1f = T 2f . Increasing entropy Q in a system. T . R l
Applications The root-mean-square speed v rms is the square root of the Molar specific heats can be predicted from the thermal energy average of the squares of the molecular speeds: because � E th = nC � T . v rms = 2 ( v 2 ) avg C V = 3 • Monatomic gas 2 R For molecules of mass m at temperature T , v rms = B C V = 5 at moderate T • Diatomic gas 2 R 3 k B T • Elemental solid C = 3 R m Terms and Notation histogram degrees of freedom entropy mean free path, l equipartition theorem second law of thermodynamics root-mean-square speed, v rms irreversible process
The goal of Chapter 19 has been to study the physical principles that govern heat engines and refrigerators. G e n er a l Pri n ci ples Heat Engines Refrigerators Devices that transform heat into work. They require two energy Devices that use work to transfer heat from a colder object to a reservoirs at different temperatures. hotter object. Energy T H Hot reservoir T H Hot reservoir Q H � Q C � W in Energy in is exhausted to Q H Q H the hot reservoir. Cyclical process Useful work done Work must be done Cyclical process W in ( � E th ) net � 0 W out � Q H � Q C to transfer energy ( � E th ) net � 0 from cold to hot. Unused energy is Q C exhausted as waste heat. Heat energy is Q C extracted from T C Cold reservoir Cold reservoir the cold reservoir. T C Thermal efficiency Second-law limit: Second-law limit: Coefficient of performance T C h = W out = what you get h … 1 - T C K = Q C = what you get K … T H T H - T C Q H what you pay W in what you pay : . : ve 0. V , , , , . .
Recommend
More recommend