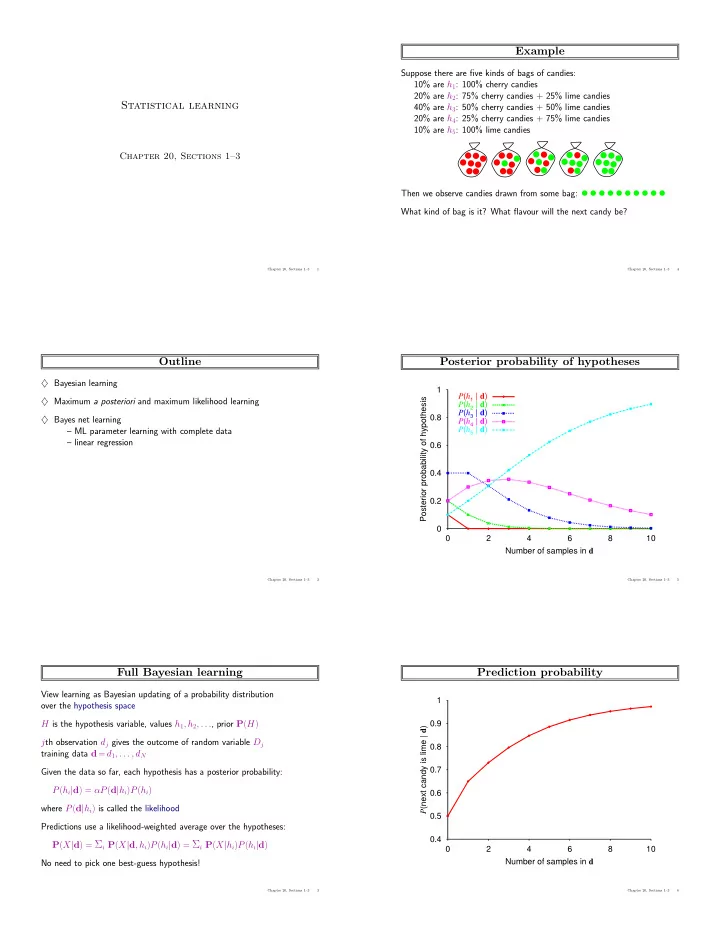
example
play

Example Suppose there are five kinds of bags of candies: 10% are h 1 - PDF document

Nov 10, 2023 •959 likes •1k views

Example Suppose there are five kinds of bags of candies: 10% are h 1 : 100% cherry candies 20% are h 2 : 75% cherry candies + 25% lime candies Statistical learning 40% are h 3 : 50% cherry candies + 50% lime candies 20% are h 4 : 25% cherry

  1. Example Suppose there are five kinds of bags of candies: 10% are h 1 : 100% cherry candies 20% are h 2 : 75% cherry candies + 25% lime candies Statistical learning 40% are h 3 : 50% cherry candies + 50% lime candies 20% are h 4 : 25% cherry candies + 75% lime candies 10% are h 5 : 100% lime candies Chapter 20, Sections 1–3 Then we observe candies drawn from some bag: What kind of bag is it? What flavour will the next candy be? Chapter 20, Sections 1–3 1 Chapter 20, Sections 1–3 4 Outline Posterior probability of hypotheses ♦ Bayesian learning 1 P ( h 1 | d ) ♦ Maximum a posteriori and maximum likelihood learning Posterior probability of hypothesis P ( h 2 | d ) P ( h 3 | d ) 0.8 P ( h 4 | d ) ♦ Bayes net learning P ( h 5 | d ) – ML parameter learning with complete data – linear regression 0.6 0.4 0.2 0 0 2 4 6 8 10 Number of samples in d Chapter 20, Sections 1–3 2 Chapter 20, Sections 1–3 5 Full Bayesian learning Prediction probability View learning as Bayesian updating of a probability distribution 1 over the hypothesis space 0.9 H is the hypothesis variable, values h 1 , h 2 , . . . , prior P ( H ) P (next candy is lime | d ) j th observation d j gives the outcome of random variable D j 0.8 training data d = d 1 , . . . , d N 0.7 Given the data so far, each hypothesis has a posterior probability: P ( h i | d ) = αP ( d | h i ) P ( h i ) 0.6 where P ( d | h i ) is called the likelihood 0.5 Predictions use a likelihood-weighted average over the hypotheses: 0.4 P ( X | d ) = Σ i P ( X | d , h i ) P ( h i | d ) = Σ i P ( X | h i ) P ( h i | d ) 0 2 4 6 8 10 Number of samples in d No need to pick one best-guess hypothesis! Chapter 20, Sections 1–3 3 Chapter 20, Sections 1–3 6

  2. MAP approximation Multiple parameters Summing over the hypothesis space is often intractable ( ) Red/green wrapper depends probabilistically on flavor: P F=cherry θ (e.g., 18,446,744,073,709,551,616 Boolean functions of 6 attributes) Likelihood for, e.g., cherry candy in green wrapper: Flavor Maximum a posteriori (MAP) learning: choose h MAP maximizing P ( h i | d ) P ( F = cherry , W = green | h θ,θ 1 ,θ 2 ) F P ( W=red | F ) θ I.e., maximize P ( d | h i ) P ( h i ) or log P ( d | h i ) + log P ( h i ) cherry = P ( F = cherry | h θ,θ 1 ,θ 2 ) P ( W = green | F = cherry , h θ,θ 1 ,θ 2 ) 1 θ lime = θ · (1 − θ 1 ) 2 Log terms can be viewed as (negative of) Wrapper bits to encode data given hypothesis + bits to encode hypothesis N candies, r c red-wrapped cherry candies, etc.: This is the basic idea of minimum description length (MDL) learning P ( d | h θ,θ 1 ,θ 2 ) = θ c (1 − θ ) ℓ · θ r c 1 (1 − θ 1 ) g c · θ r ℓ 2 (1 − θ 2 ) g ℓ For deterministic hypotheses, P ( d | h i ) is 1 if consistent, 0 otherwise ⇒ MAP = simplest consistent hypothesis (cf. science) L = [ c log θ + ℓ log(1 − θ )] + [ r c log θ 1 + g c log(1 − θ 1 )] + [ r ℓ log θ 2 + g ℓ log(1 − θ 2 )] Chapter 20, Sections 1–3 7 Chapter 20, Sections 1–3 10 ML approximation Multiple parameters contd. For large data sets, prior becomes irrelevant Derivatives of L contain only the relevant parameter: ∂L ∂θ = c ℓ c Maximum likelihood (ML) learning: choose h ML maximizing P ( d | h i ) θ − 1 − θ = 0 ⇒ θ = c + ℓ I.e., simply get the best fit to the data; identical to MAP for uniform prior (which is reasonable if all hypotheses are of the same complexity) ∂L = r c g c r c − = 0 ⇒ θ 1 = ML is the “standard” (non-Bayesian) statistical learning method ∂θ 1 θ 1 1 − θ 1 r c + g c ∂L = r ℓ g ℓ r ℓ − = 0 ⇒ θ 2 = ∂θ 2 θ 2 1 − θ 2 r ℓ + g ℓ With complete data, parameters can be learned separately Chapter 20, Sections 1–3 8 Chapter 20, Sections 1–3 11 ML parameter learning in Bayes nets Example: linear Gaussian model 1 Bag from a new manufacturer; fraction θ of cherry candies? 0.8 P F=cherry ( ) Any θ is possible: continuum of hypotheses h θ θ P ( y | x ) 4 0.6 θ is a parameter for this simple (binomial) family of models 3.5 3 y Flavor 2.5 0.4 2 Suppose we unwrap N candies, c cherries and ℓ = N − c limes 1.5 1 0 0.20.40.60.81 0.5 0.2 These are i.i.d. (independent, identically distributed) observations, so 0 0 0.2 y 0.4 0.6 0 0.8 1 N x j = 1 P ( d j | h θ ) = θ c · (1 − θ ) ℓ 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 P ( d | h θ ) = � x 2 πσe − ( y − ( θ 1 x + θ 2))2 1 Maximize this w.r.t. θ —which is easier for the log-likelihood: √ Maximizing P ( y | x ) = 2 σ 2 w.r.t. θ 1 , θ 2 N L ( d | h θ ) = log P ( d | h θ ) = j = 1 log P ( d j | h θ ) = c log θ + ℓ log(1 − θ ) � N j = 1 ( y j − ( θ 1 x j + θ 2 )) 2 = minimizing E = � dL ( d | h θ ) = c ℓ c + ℓ = c c θ − 1 − θ = 0 ⇒ θ = dθ N That is, minimizing the sum of squared errors gives the ML solution Seems sensible, but causes problems with 0 counts! for a linear fit assuming Gaussian noise of fixed variance Chapter 20, Sections 1–3 9 Chapter 20, Sections 1–3 12

  3. Summary Full Bayesian learning gives best possible predictions but is intractable MAP learning balances complexity with accuracy on training data Maximum likelihood assumes uniform prior, OK for large data sets 1. Choose a parameterized family of models to describe the data requires substantial insight and sometimes new models 2. Write down the likelihood of the data as a function of the parameters may require summing over hidden variables, i.e., inference 3. Write down the derivative of the log likelihood w.r.t. each parameter 4. Find the parameter values such that the derivatives are zero may be hard/impossible; modern optimization techniques help Chapter 20, Sections 1–3 13

Recommend

More recommend