= E V V w T ( ) w e ( ) ( ( ) ) = Def. Def. A A - PDF document

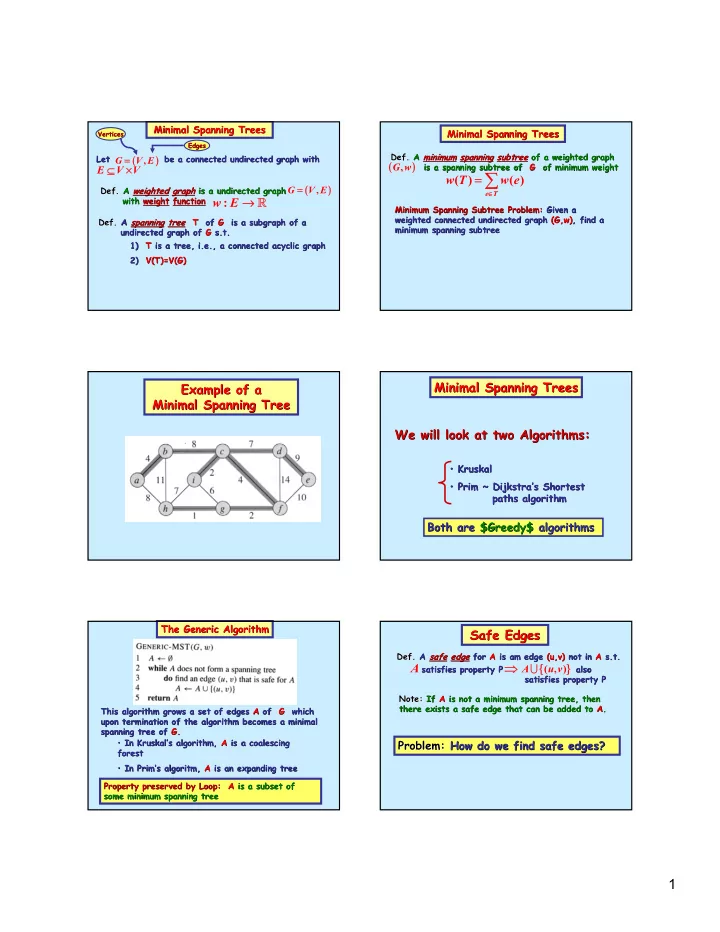
Minimal Spanning Trees Minimal Spanning Trees Minimal Spanning Trees Minimal Spanning Trees Vertices Vertices Edges Edges Def. Def. A A minimum minimum spanning spanning subtree subtree of a weighted graph of a weighted graph Let be a connected undirected graph with ( ( ) ) Let be a connected undirected graph with = G V E , ( ( ) ) is a spanning is a spanning subtree subtree of of G G of minimum weight of minimum weight ⊆ ⊆ × × G w , = ∑ E V V w T ( ) w e ( ) ( ( ) ) = Def. Def. A A weighted weighted graph graph is a undirected graph is a undirected graph G V E , ∈ e T w E → � with with weight weight function function : Minimum Spanning Subtree Subtree Problem: Problem: Given a Given a Minimum Spanning weighted connected undirected graph weighted connected undirected graph ( (G,w G,w) ), find a , find a Def. Def. A A spanning spanning tree tree T T of G of G is a is a subgraph subgraph of of a a minimum spanning subtree subtree minimum spanning undirected graph of undirected graph of G G s.t s.t. . 1) T 1) T is a tree, i.e., a connected acyclic graph is a tree, i.e., a connected acyclic graph 2) V(T)=V(G) 2) V(T)=V(G) Minimal Spanning Trees Minimal Spanning Trees Example of a Example of a Minimal Spanning Tree Minimal Spanning Tree We will look at two Algorithms: We will look at two Algorithms: • • Kruskal Kruskal • • Prim ~ Prim ~ Dijkstra Dijkstra’ ’s s Shortest Shortest paths algorithm paths algorithm Both are $Greedy$ $Greedy$ algorithms algorithms Both are The Generic Algorithm The Generic Algorithm Safe Edges Safe Edges Def. A Def. A safe safe edge edge for for A A is am edge is am edge ( (u,v u,v) ) not in not in A A s.t s.t. . ⇒ { } A satisfies property P also A satisfies property P also ∪ A A ( , ) u v satisfies property P satisfies property P Note: If Note: If A A is not a minimum spanning tree, then is not a minimum spanning tree, then there exists a safe edge that can be added to A A. . there exists a safe edge that can be added to This algorithm grows a set of edges A This algorithm grows a set of edges A of of G G which which upon termination of the algorithm becomes a minimal upon termination of the algorithm becomes a minimal spanning tree of G spanning tree of G. . • In • In Kruskal Kruskal’ ’s s algorithm, algorithm, A A is a coalescing is a coalescing Problem: How do we find safe edges? Problem: How do we find safe edges? forest forest • In • In Prim Prim’ ’s s algoritm algoritm, , A A is an expanding tree is an expanding tree Property preserved by Loop: Property preserved by Loop: A is a subset of A is a subset of some minimum spanning tree some minimum spanning tree 1

Terminology Terminology More Terminology More Terminology Def. Def. An edge crossing a cut (S,V An edge crossing a cut (S,V- -S) S) of a weighted of a weighted Def. A cut cut (S,V (S,V- -S) S) of an undirected graph of an undirected graph Def. A undirected graph ( undirected graph (G,w G,w) ) is a is a light light edge edge if its weight if its weight G=(V,E) G=(V,E) is a is a partion partion of the vertices V of G into two of the vertices V of G into two is minimum of the weight of any edge crossing the is minimum of the weight of any edge crossing the disjoint sets S S and and V V- -S S, i.e., , i.e., s.t s.t. . disjoint sets • • cut. cut. = = − − ∪ V S ( V S ) • • ∅ = ∅ = − ∩ S ( V S ) Note: Note: An edge is a light An edge is a light edge edge satisfying satisfying property property P P if its weight is the minimum of any edge satisfying if its weight is the minimum of any edge satisfying property P. property P. ∈ An edge An edge crosses crosses the cut the cut (S,V (S,V- -S) S) if one of if one of ( , ) u v E its endpoints lies in S its endpoints lies in S and the other lies in and the other lies in V V- -S S. . A cut respects respects a set of edges a set of edges A A of of G G if no edge of if no edge of A cut A A crosses the cut. crosses the cut. Example of a Cut Example of a Cut Minimal Spanning Trees Minimal Spanning Trees • • G=(V,E) G=(V,E) connected a connected a undir undir graph graph Theorem. Theorem. Given Given • • w:E w:E � � R R a weight function on a weight function on G G • • ⊆ A E be s.t s.t. . A A lies in some minimum lies in some minimum be Let Let spanning tree spanning tree • (S,V • (S,V- -S) S) be a cut of be a cut of G G that respects that respects A A • ( • (u,v u,v) ) be a light edge crossing be a light edge crossing (S,V (S,V- -S) S) Then Then ( (u,v u,v) ) is safe! is safe! Proof Proof Kruskal Kruskal’ ’s s Algorithm Algorithm Cor Cor. . Given Given (G=( (G=(V,E),w V,E),w) ) is a connected is a connected undirected weighted graph. undirected weighted graph. Let Let A A be a subset of be a subset of E E lying in a minimum lying in a minimum weight subtree subtree of of G G, and let , and let C C be a be a weight connected component of a forest G G A =(V,A). connected component of a forest A =(V,A). If ( (u,v u,v) ) is a light edge connecting C to some is a light edge connecting C to some If other component of G G A , then ( (u,v u,v) ) is safe for is safe for other component of A , then A A A= Shaded Edges A= Shaded Edges 2

Kruskal Kruskal’ ’s s Algorithm Algorithm Kruskal Kruskal’ ’s s Algorithm Algorithm Prim’ Prim ’s s Algorithm Algorithm Kruskal’ Kruskal ’s s Algorithm (Cont.) Algorithm (Cont.) 3