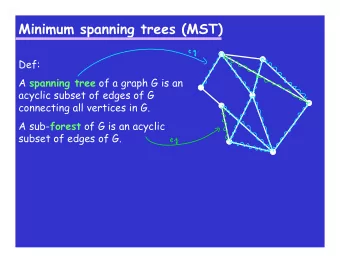
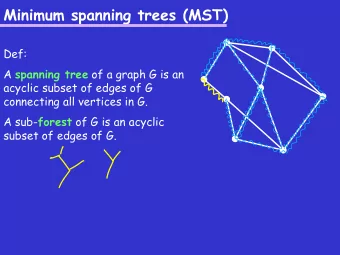
Tree Introduction to Algorithms Introduction to Algorithms � We call an undirected graph a tree if the graph � We call an undirected graph a tree if the graph is connected and contains no cycles . Spanning Trees Spanning Trees g � Trees: CSE 680 � Not Trees: Prof. Roger Crawfis Not Has a connected cycle cycle Number of Vertices Connected Graph p � If a graph is a tree then the number of � If a graph is a tree, then the number of � A connected graph is one in which � A connected graph is one in which edges in the graph is one less than the there is at least one path between each number of vertices number of vertices. pair of vertices pair of vertices. � A tree with n vertices has n – 1 edges. � Each node has one parent except for the root. � Note: Any node can be the root here, as we are not dealing with rooted trees.
Spanning Tree p g Non-Connected Graphs p � In a tree there is always exactly one path from each y y p � If the graph is not connected, we get a � If the graph is not connected we get a vertex in the graph to any other vertex in the graph. spanning tree for each connected � A spanning tree for a graph is a subgraph that component of the graph component of the graph. includes every vertex of the original, and is a tree. i l d t f th i i l d i t � That is we get a forest. (c) Depth-first ( ) p (a) Graph G (a) Graph G (b) (b) Breadth-first ead s spanning tree of spanning tree of G rooted at c G rooted at b Finding a Spanning Tree g p g Minimum Spanning Tree p g � A spanning tree that has minimum total weight is p g g Find a spanning tree for the graph below. p g g p called a minimum spanning tree for the graph. � Technically it is a minimum-weight spanning tree. � If all edges have the same weight breadth-first � If all edges have the same weight, breadth first search or depth-first search will yield minimum spanning trees. We could break the two cycles by removing a single edge from each. We could break the two cycles by removing a single edge from each. � For the rest of this discussion, we assume the � For the rest of this discussion we assume the One of several possible ways to do this is shown below. edges have weights associated with them. Was breadth first or Was breadth-first or Note, we are strictly dealing with undirected graphs here, for directed depth-first search (or graphs we would want to find the optimum branching or neither) used to aborescence of the directed graph. create this?
Minimum Spanning Tree p g Minimum Spanning Tree p g � Minimum-cost spanning trees have many Minimum cost spanning trees have many � Consider this graph. Consider this graph. applications. � Building cable networks that join n locations � It has 16 spanning trees. Some are: � It has 16 spanning trees Some are: with minimum cost. � Building a road network that joins n cities with minimum cost minimum cost. � Obtaining an independent set of circuit equations for an electrical network. � There are two minimum- � There are two minimum- � In pattern recognition minimal spanning trees cost spanning trees, can be used to find noisy pixels. each with a cost of 6: Minimum Spanning Tree p g Brute Force MST � Brute Force option: Brute Force option: � For a complete graph, it has been shown � For a complete graph, it has been shown that there are N N-2 possible spanning For all possible spanning trees 1. Calculate the sum of the edge weights trees! i. Keep track of the tree with the minimum weight. ii. � Alternatively, given N items, you can � Step i) requires N-1 time, since each tree build N N-2 distinct trees to connect these will have exactly N 1 edges will have exactly N-1 edges. items. � If there are M spanning trees, then the � Note, for a lattice (like your grid ( y g total cost will O(MN). total cost will O(MN) implementation), the number of spanning � Consider a complete graph, with N(N-1) trees is O ( e 1.167 N ). edges. How big can M be? edges. How big can M be?
Minimum Spanning Tree p g Kruskal’s Algorithm � There are many approaches to computing a y pp p g � Greedy algorithm to choose the edges as follows. y g g minimum spanning tree. We could try to detect cycles and remove edges, but the two Step 1 First edge: choose any edge with the minimum weight. algorithms we will study build them from the g y bottom-up in a greedy fashion. Step 2 Next edge: choose any edge with minimum weight from those not yet selected . (The subgraph can look � Kruskal’s Algorithm – starts with a forest of disconnected at this stage.) single node trees and then adds the edge with single node trees and then adds the edge with the minimum weight to connect two Step 3 Continue to choose edges of minimum weight from those components. not yet selected, except do not select any edge that creates a cycle in the subgraph. � Prim s Algorithm – starts with a single vertex � Prim’s Algorithm starts with a single vertex and then adds the minimum edge to extend the Step 4 Repeat step 3 until the subgraph connects all vertices of spanning tree. the original graph. Kruskal’s Algorithm g Kruskal’s Algorithm g Solution Solution Use Kruskal’s algorithm to find a minimum spanning tree for the Use Kruskal s algorithm to find a minimum spanning tree for the graph. First, choose ED (the smallest weight). 1 1 E 1 7 D E 7 D D 4 5 4.5 A F 9.5 3 4.5 10 A F 9.5 3 10 7.5 7.5 1 5 1.5 4 4 7.5 1.5 4 C B 8 C B 8 8
Kruskal’s Algorithm g Kruskal’s Algorithm g Solution Solution Solution Solution Now choose BF (the smallest remaining weight). Now CD and then BD. 1 1 E E 7 7 D D D D 4.5 4.5 A F 9.5 3 A F 9.5 3 10 10 7.5 7.5 1.5 4 1.5 4 C C B B 8 8 8 8 Kruskal’s Algorithm g Kruskal’s Algorithm g Solution Solution Solution Solution Note EF is the smallest remaining, but that would create a cycle. The total weight of the tree is 16.5. Choose AE and we are done. 1 1 E E 7 7 D D D D 4.5 4.5 A F 9.5 3 A F 9.5 3 10 10 7.5 7.5 1.5 4 1.5 4 C C B B 8 8 8 8
Kruskal’s Algorithm g Kruskal’s Algorithm g Build a priority queue (min-based) with all of the edges of G. � Some questions: � Some questions: T = φ ; How do we know we are finished? while(queue is not empty){ 1. get minimum edge e from priorityQueue; How do we check for cycles? How do we check for cycles? 2 2. if( if(e does not create a cycle with edges in T) d t t l ith d i T) 1 add e to T; E } 7 D D return T; return T; 4.5 A F 9.5 3 10 7.5 1.5 4 C B 8 8 Kruskal’s Algorithm g Kruskal’s Algorithm – Time complexity � Steps p � Initialize forest O( |V| ) � Sort edges O( |E| log |E| ) � Check edge for cycles O( |V| ) x Check edge for cycles O( |V| ) x � Trace of Kruskal's algorithm for O( |V| 2 ) � Number of edges O( |V| ) the undirected, weighted graph: � Total O( |V|+|E| log |E|+|V| 2 ) � Since |E| = O( |V| 2 ) O( |V| 2 log |V| ) � Thus we would class MST as O( n 2 log n ) for a graph with n ( g ) vertices � This is an upper bound , some improvements on this are known. The minimum cost is: 24 The minimum cost is: 24
Kruskal’s Algorithm g Kruskal’s Algorithm g � Another implementation is based on sets (see Chapter 21). Kruskal() { 2 19 T = ∅ ; 9 for each v ∈ V 14 17 8 25 MakeSet(v); 5 sort E by increasing edge weight w for each (u,v) ∈ E (in sorted order) 21 13 1 if FindSet(u) ≠ FindSet(v) T = T U {{u,v}}; {{ , }} Union(FindSet(u), FindSet(v)); } Kruskal’s Algorithm g Kruskal’s Algorithm g 2 19 2 19 9 9 14 17 14 17 8 25 8 25 5 5 21 13 21 13 1? 1 1? 1
Kruskal’s Algorithm g Kruskal’s Algorithm g 2 19 2 19 9 9 14 17 14 17 8 25 8 25 5 5 21 13 21 13 1? 1 1? 1 Kruskal’s Algorithm g Kruskal’s Algorithm g 2 19 2 19 9 9 14 17 14 17 8 25 8 25 5 5 21 13 21 13 1? 1 1? 1
Kruskal’s Algorithm g Prim’s Algorithm g � Prim’s algorithm finds a minimum cost spanning tree b by selecting edges from the graph one-by-one as l i d f h h b follows: 2 19 � It starts with a tree, T, consisting of a single starting 9 vertex, x. 14 17 8 25 � Then, it finds the shortest edge emanating from x 5 that connects T to the rest of the graph (i.e., a vertex g p ( not in the tree T). 21 13 1? 1 � It adds this edge and the new vertex to the tree T. � It then picks the shortest edge emanating from the � It then picks the shortest edge emanating from the revised tree T that also connects T to the rest of the graph and repeats the process. Prim’s Algorithm Abstract g Prim’s Algorithm g Consider a graph G=(V E); Consider a graph G (V, E); Let T be a tree consisting of only the starting 2 19 vertex x; vertex x; 9 14 17 Start here 8 25 while (T has fewer than I V I vertices) 5 { 21 13 1 find a smallest edge connecting T to G-T; add it to T; dd i T }
Prim’s Algorithm g Prim’s Algorithm g 2 19 2 19 9 9 14 17 14 17 8 25 8 25 5 5 21 13 21 13 1? 1 1 Prim’s Algorithm g Prim’s Algorithm g 2 19 2 19 9 9 9 14 17 14 17 8 25 8 25 5 5 21 13 21 13 1 1
Recommend
More recommend
