e d
play

E D C C M M or A A K K 1) Move the coins out of E make it - PowerPoint PPT Presentation

Jul 13, 2023 •313 likes •473 views

N N $ E D C C M M or A A K K 1) Move the coins out of E make it deterministic [RBBK0 1] To improve resistance to random-number generation problems To architect to existing abstraction boundaries 2) Add in associated data

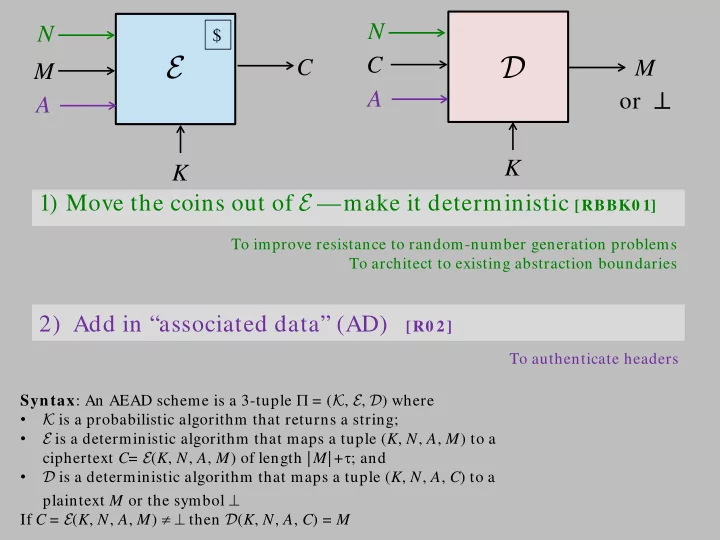
  1. N N $ E D C C M M or ⊥ A A K K 1) Move the coins out of E —make it deterministic [RBBK0 1] To improve resistance to random-number generation problems To architect to existing abstraction boundaries 2) Add in “associated data” (AD) [R0 2] To authenticate headers Syntax : An AEAD scheme is a 3-tuple Π = ( K , E , D ) where • K is a probabilistic algorithm that returns a string; • E is a deterministic algorithm that maps a tuple ( K , N , A , M ) to a ciphertext C = E ( K , N , A , M ) of length | M | + τ ; and • D is a deterministic algorithm that maps a tuple ( K , N , A , C ) to a plaintext M or the symbol ⊥ 1 If C = E ( K , N , A , M ) ≠ ⊥ then D ( K , N , A , C ) = M X

  2. N , A , M K ( ⋅,⋅,⋅ ) $ ( ⋅,⋅,⋅ ) E C C A ⊥ M ⊥ ( ⋅,⋅,⋅ ) K ( ⋅,⋅,⋅ ) D N , A , C $, ⊥ aead E K , D K  1] I − Pr[ A  1] ( A ) = Pr[ A Adv E A may not: - Repeat an N in an enc query - Ask a dec query ( N, A, C ) after C is returned by an ( N , A , ⋅ ) enc query 2

  3. N , A , M K ( ⋅,⋅,⋅ ) $ ( ⋅,⋅,⋅ ) E C C A E K $ priv  1] I − Pr[ A  1] ( A ) = Pr[ A Adv E A may not: - Ask a dec query ( N, A, C ) after C is returned by an ( N , A , ⋅ ) enc query 3

  4. N , A , M K ( ⋅,⋅,⋅ ) E C A N*, A*, C* E K auth ( A ) = Pr[ A forges] I Adv E It outputs an ( N* , A* , C* ) where D ( K , N* , A* , C* ) ≠⊥ and no prior oracle query of ( N* , A* , M ) returned C* 4

  5. All-in-one definition Adv aead ( A ) = Pr[ A E ( K , ... ), D ( K , ... ) ⇒ 1] − Pr[ A $( ... ), ⊥ ( ... ) ⇒ 1] Π A may not repeat any N query to its Enc oracle. It may not ask Dec( N , A , C ) after an Enc( N , A , M ) returned C. Two-part definition Adv priv ( A ) = Pr[ A E ( K , ... ) ⇒ 1] − Pr[ A $( ... ) ⇒ 1] Π A may not repeat any N query. Adv auth ( A ) = Pr[ A E ( K , ... ) forges ] Π It outputs an ( N , A , C ) where D ( K , N , A , C ) ≠⊥ and no prior oracle query of ( N , A , M ) returned C 5

  6. [Bellare, Nam prem pre 20 0 0 ] Generic com position M M M E K $ $ E K F L F L C T E K $ F L T C C  MAC-then-Encrypt Encrypt-then-MAC Encrypt-and-MAC 6

  7. SIV m ode [Rogaway, Shrimpton 2006] N A M ivE encryption scheme (eg, CTR), secure E K 2 IV f K 1 C PRF operating on a vector of strings 7

  8. [Gueron, Langley, Lindell 2017] AES-GCM-SIV [Bose, Hoang, Tessaro 2018] R 64 (AES K ( N 2 )) K R 64 (AES K ( N 3 )) DeriveKey AES K 2 T N R 64 (AES K ( N 0 )) ⊕ S 0 R 127 ( S ) 0 N R 64 (AES K ( N 1 )) Close to GHASH but adjusted to better match AES-NI: Σ α i M i K 1 i K 1 POLYVAL Hash A 0 M 0 a m a m ⊕ C Pad AES AES AES AES K 2 Additions: no carry out of last 32 bits 1 R 127 ( T ) 1 R 127 ( T )+1 1 R 127 ( T )+2 1 R 127 ( T )+3 8

  9. CCM [Whiting, Housley, Ferguson 2002] NIST SP 800-38C RFC 3610, 4309, 5084 CCM is provably secure if E is a good PRP. Thm [Jonsson 2002] 9

  10. GCM [McGrew, Viega 2004] (Follows CWC [Kohno, Viega, Whiting 2004]) NIST SP 800-38D:2007 RFC 4106, 5084, 5116, 5288, 5647 ISO 19772:2009 Thm [Iwata , Ohashi , and Minematsu 2012] (correcting [McGrew, Viega 2004]) GCM is provably secure (not great bounds) if E is a good PRP. 10

  11. OCB (v3) Thm [Krovetz, Rogaway 2011] [Krovetz Rogaway 2011] , following OCB is provably secure (OK bounds) if E is a strong PRP. [RBBK01,LRW02,R04] RFC 7253 11

  12. [Liskov, Rivest, Wagner 2002] Tweakable Blockcipher (TBC) ~ E : K × T × {0,1} n → {0,1} n A T -indexed family of ~ ~ T each E K ( ⋅ ) = E ( K , T , ⋅ ) a perm utation random permutations on n bits π ~ E K A ~ T Y = E K ( X ) 1 or 0 Adv ( A ) = Pr [ A E K ⇒ 1] – Pr [ A π ⇒ 1] ~ prp ~ E 12

  13. This is the official public announcement of the portfolio, bringing the CAESAR competition to a close. … [H]ere is the final portfolio: Use case 1: Ascon first choice, ACORN second choice. 57 round-1 Use case 2: AEGIS-128 and OCB , without a preference. (Mar 2014) Use case 3: Deoxys-II first choice, COLM second choice. 29 round-2 (Mar 2014) 16 round-3 (Aug 2016) 7 finalists (Mar 2018) 6 winners (Feb 209) 13

  14. Thm : Provably secure, with excellent Deoxys-II Jean, Nikolić , bounds, if E is a TBC. Peyrin, Seurin T A 1 A 2 A 3 E 1$ E 2$ E 3$ E N & K K K K ⊕ ⊕ ⊕ ⊕ E 1# E 2# E 3# E 4# K K K K M 1 M 2 M 3 M 4 E T ⊕ 1 E T ⊕2 E T ⊕ 3 E T ⊕ 4 ⊕ ⊕ ⊕ ⊕ 〈 N 〉 〈 N 〉 〈 N 〉 〈 N 〉 K K K K C 1 C 2 C 3 C 4 14

  15. 0 .4 3 cpb (Skylake) AEGIS The fastest ( 0 .25 cpb for AEGIS-128 L CAESAR finalist on 16K messages) AEGIS-128 [Wu, Preneel 20 13] on recent Intel processors P 0 P 1 P 2 P 3 P 4 P 5 P 6 P 7 P 8 T C 0 C 1 C 2 C 3 C 4 C 5 C 6 C 7 C 8 B ⊕ CD ⊕ E A A K , N , A dependent initialization B B | A | , | P | dependent tag computation C C D D E E 4 5 6 7 8 9 10 11 12 15

Recommend

More recommend