Determining the solution Variable number of segments When Opt[ k - PDF document

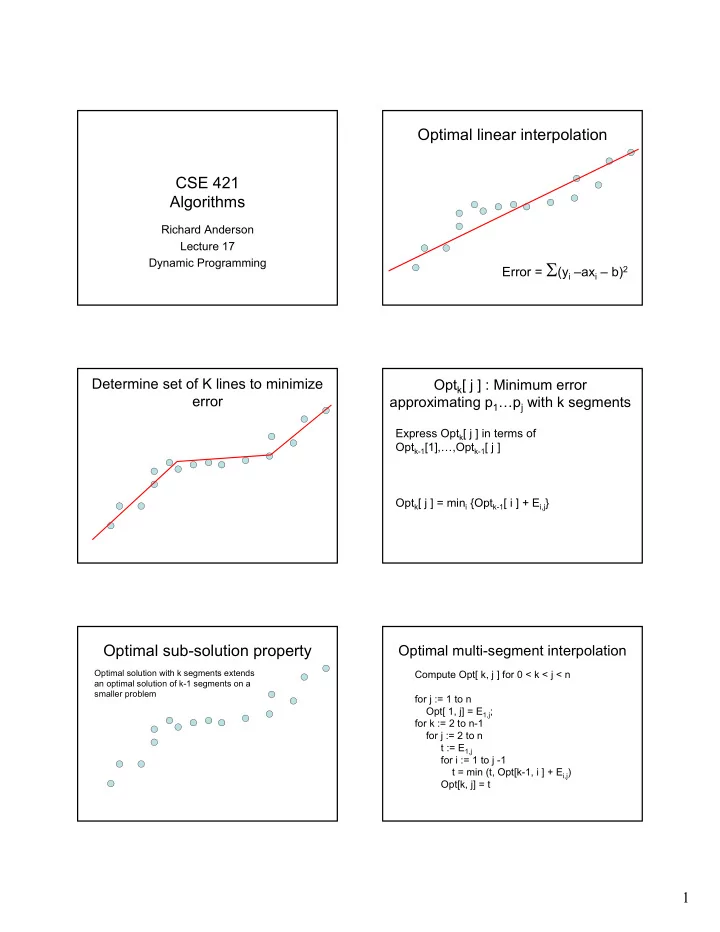
Optimal linear interpolation CSE 421 Algorithms Richard Anderson Lecture 17 Dynamic Programming Error = Σ (y i –ax i – b) 2 Determine set of K lines to minimize Opt k [ j ] : Minimum error error approximating p 1 …p j with k segments Express Opt k [ j ] in terms of Opt k-1 [1],…,Opt k-1 [ j ] Opt k [ j ] = min i {Opt k-1 [ i ] + E i,j } Optimal sub-solution property Optimal multi-segment interpolation Optimal solution with k segments extends Compute Opt[ k, j ] for 0 < k < j < n an optimal solution of k-1 segments on a smaller problem for j := 1 to n Opt[ 1, j] = E 1,j ; for k := 2 to n-1 for j := 2 to n t := E 1,j for i := 1 to j -1 t = min (t, Opt[k-1, i ] + E i,j ) Opt[k, j] = t 1

Determining the solution Variable number of segments • When Opt[ k ,j ] is computed, record the • Segments not specified in advance value of i that minimized the sum • Penalty function associated with segments • Store this value in a auxiliary array • Cost = Interpolation error + C x #Segments • Use to reconstruct solution Penalty cost measure Subset Sum Problem • Opt[ j ] = min(E 1,j , min i (Opt[ i ] + E i,j )) + P • Let w 1 ,…,w n = {6, 8, 9, 11, 13, 16, 18, 24} • Find a subset that has as large a sum as possible, without exceeding 50 Adding a variable for Weight Subset Sum Recurrence • Opt[ j, K ] the largest subset of {w 1 , …, w j } • Opt[ j, K ] the largest subset of {w 1 , …, w j } that sums to at most K that sums to at most K • {2, 4, 7, 10} – Opt[2, 7] = – Opt[3, 7] = – Opt[3,12] = – Opt[4,12] = 2

Subset Sum Grid Subset Sum Code Opt[ j, K] = max(Opt[ j – 1, K], Opt[ j – 1, K – w j ] + w j ) 4 3 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 {2, 4, 7, 10} Knapsack Problem Knapsack Recurrence Subset Sum Recurrence: • Items have weights and values • The problem is to maximize total value subject to Opt[ j, K] = max(Opt[ j – 1, K], Opt[ j – 1, K – w j ] + w j ) a bound on weght • Items {I 1 , I 2 , … I n } Knapsack Recurrence: – Weights {w 1 , w 2 , …,w n } – Values {v 1 , v 2 , …, v n } – Bound K • Find set S of indices to: – Maximize Σ i ε S v i such that Σ i ε S w i <= K Knapsack Grid Opt[ j, K] = max(Opt[ j – 1, K], Opt[ j – 1, K – w j ] + v j ) 4 3 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Weights {2, 4, 7, 10} Values: {3, 5, 9, 16} 3