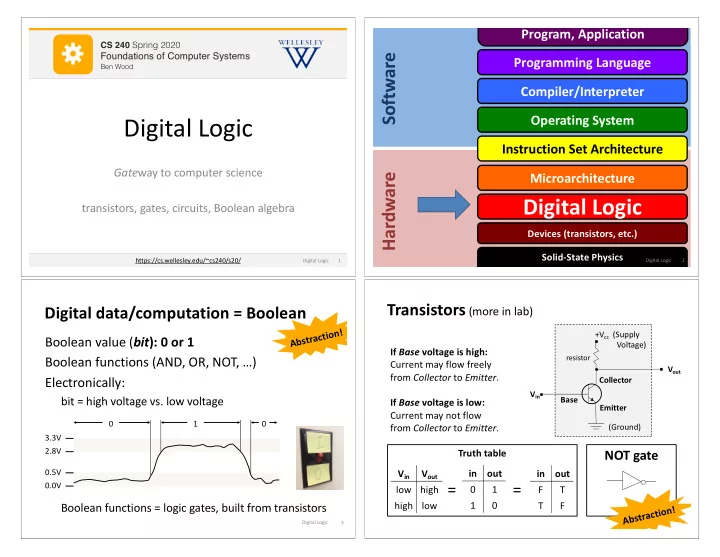

Program, Application λ CS 251 Fall 2019 CS 240 Spring 2020 Principles of Programming Languages Foundations of Computer Systems Software Programming Language Ben Wood Ben Wood Compiler/Interpreter Digital Logic Operating System Instruction Set Architecture Gate way to computer science Microarchitecture Hardware Digital Logic transistors, gates, circuits, Boolean algebra Devices (transistors, etc.) Solid-State Physics https://cs.wellesley.edu/~cs240/s20/ Digital Logic 1 Digital Logic 2 Transistors (more in lab) Digital data/computation = Boolean Abstraction! +V cc (Supply Boolean value ( bit ): 0 or 1 Voltage) If Base voltage is high: Boolean functions (AND, OR, NOT, …) resistor Current may flow freely V out from Collector to Emitter . Electronically: Collector V in bit = high voltage vs. low voltage Base If Base voltage is low: Emitter Current may not flow 0 1 0 from Collector to Emitter . (Ground) 3.3V 2.8V NOT gate Truth table 0.5V V in V out in out in out = = 0.0V low high 0 1 F T high low 1 0 T F Boolean functions = logic gates, built from transistors Abstraction! Digital Logic 3 Digital Logic 4
ex Abstraction! Digital Logic Gates Integrated Circuits (1950s - ) Tiny electronic devices that compute basic Boolean functions. Early (first?) transistor Chip NOT NAND V 2 V in V out 0 1 Wafer + V cc 0 1 0 V 1 Small integrated circuit 1 0 1 + V cc V out V 1 V out V 2 V in Digital Logic 5 Digital Logic 6 inputs = variables ex Boolean Algebra Five basic gates: define with truth tables wires = expressions gates = operators/functions for combinational logic circuits = functions A A A + B A B B B 0 1 0 1 NOT NAND NOR (A · B) AND = Boolean product OR = Boolean sum 0 1 0 1 1 0 · 0 1 1 0 1 1 0 1 + 0 1 0 0 0 0 0 1 1 0 1 1 1 1 0 1 0 1 AND OR A A A A 0 0 NOT = inverse or complement wire = identity 1 1 0 1 0 0 1 0 1 1 Digital Logic 7 Digital Logic 8
ex ex Circuits Translation Connect inputs and outputs of gates with wires. Connect gates to implement these functions. Check with truth tables. Use a direct translation -- it is straightforward and bidirectional. Crossed wires touch only if there is a dot. F = (AB + C)D A B = C Z = W + (X + WY) What is the output if A=1, B=0, C=1? What is the truth table of this circuit? What is an equivalent Boolean expression? Digital Logic 9 Digital Logic 10 Note on notation: bubble = inverse/complement Commutativity, Associativity A + B A + B A A = B B A B A + B B + A = Identity law, inverse law B A 0 0 + A = A A A AB A(BC) A A (AB)C B BC = B C C A A 0 = A A Digital Logic 11 Digital Logic 12
Idempotent law, Null/Zero law Note on notation: bubble = inverse/complement A A A + B = A + B B B A + A A = A A DeMorgan's Law ( double bubble , toil and trouble, in Randy's words...) AB 0 1 A = A B 0 1 1 0 B 0 A 0 1 1 0 = A A A+B 0 1 A A + B = 0 1 0 B 1 0 0 Digital Logic 13 Digital Logic 14 One law, Absorption law ex ex NAND is universal . Write truth tables. Do they correspond to simpler circuits? All Boolean functions can be implemented using only NANDs. Build NOT, AND, OR, NOR, using only NAND gates. A A + 1 = 1 A + AB A = B AB Digital Logic 15 Digital Logic 16
ex ex XOR: Exclusive OR Larger gates Output = 1 if exactly one input = 1. Build a 4-input AND gate using any number of 2-input gates. Truth table: Build from earlier gates: Often used as a one-bit comparator. Digital Logic 17 Digital Logic 19 Why simplify? ex ex Circuit simplification Circuit derivation: code detectors Smaller = cheaper, faster, cooler, easier to design/build. AND gate + NOT gates = code detector, recognizes exactly one input code. Is there a simpler circuit that performs the same function? Design a 4-input code detector to output 1 if ABCD = 1001, and 0 otherwise. A B C Start with an equivalent Boolean expression, then simplify with algebra. D F(A, B, C) = Design a 4-input code detector to accept two codes (ABCD=1001, ABCD=1111) and reject all others. (accept = 1, reject = 0) Check the answer with a truth table. Digital Logic 20 Digital Logic 21
ex ex Voting machines Circuit derivation: sum-of-products form logical sum (OR) A majority circuit outputs 1 if and only if a majority of its inputs equal 1. Design a majority circuit for three inputs. Use a sum of products. of products (AND) A B C Majority of inputs or their complements (NOT) 0 0 0 0 0 0 1 0 Draw the truth table and design a sum-of-products circuit for a 4-input code detector to accept two codes (ABCD=1001, ABCD=1111) and reject all others. 0 1 0 0 How are the truth table and the sum-of-products circuit related? 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1 Triply redundant computers in spacecraft • Space program also hastened Integrated Circuits. Digital Logic 22 Digital Logic 23 Computers Early pioneers in reliable computing Apollo 11 code print-out l Manual calculations l powered all early Katherine Johnson US space missions. l Calculated first US human space flight trajectories l Facilitated transition to l Mercury, Apollo 11, Space Shuttle, … digital computers. l Reputation for accuracy in manual calculations, verified early code l Called to verify results of code for launch calculations for first US human in orbit Katherine Johnson Mary Jackson l Backup calculations helped save Apollo 13 l Supported Mercury, Apollo, Space l Presidential Medal of Freedom 2015 Shuttle, ... Margaret Hamilton Dorothy Vaughn l Led software team for Apollo 11 Guidance Computer, averted mission l First black supervisor within NACA abort on first moon landing. l Early self-taught FORTRAN l Coined “software engineering”, programmer for NASA move to digital developed techniques for correctness and computers. reliability. Digital Logic 24 Digital Logic 25 l Presidential Medal of Freedom 2016
Recommend
More recommend