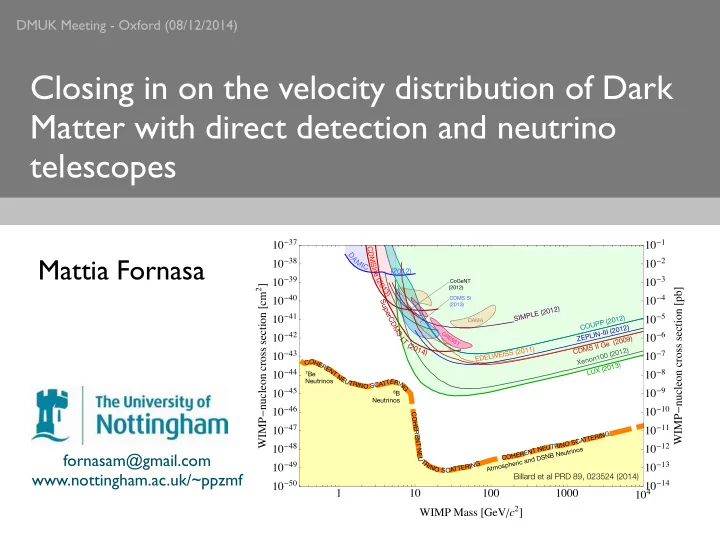

DMUK Meeting - Oxford (08/12/2014) Closing in on the velocity distribution of Dark Matter with direct detection and neutrino telescopes 10 - 37 10 - 1 C D D Mattia Fornasa A M 10 - 38 10 - 2 M I S C ( l 2 2 ) 0 1 i t e 10 - 39 ( 10 - 3 2 CoGeNT 0 WIMP - nucleon cross section @ cm 2 D 1 (2012) WIMP - nucleon cross section @ pb D 3 ) 10 - 40 10 - 4 CDMS Si S (2013) u SIMPLE (2012) p e 10 - 41 r COUPP (2012) 10 - 5 C DAMA D ZEPLIN-III (2012) M S C 10 - 42 10 - 6 R E CDMS II Ge (2009) L S T S T ( 2 0 ) 1 1 1 Xenon100 (2012) 0 4 2 ) ( S S 10 - 43 E I 10 - 7 W L E D E O C H E LUX (2013) R E N 10 - 44 10 - 8 T 7 Be N E Neutrinos U E T T R I T R A I C N N S O G 10 - 45 10 - 9 8 B Neutrinos 10 - 46 10 - 10 C OHE 10 - 47 10 - 11 R E G N TER I T A SC N O N R I 10 - 48 T NEU U T 10 - 12 E Atmospheric and DSNB Neutrinos N N T R E fornasam@gmail.com H E O C T I N G R I 10 - 49 10 - 13 R E N O T A T S C www.nottingham.ac.uk/~ppzmf Billard et al PRD 89, 023524 (2014) 10 - 14 10 - 50 1 10 100 1000 10 4 WIMP Mass @ GeV ê c 2 D
DMUK Meeting - Oxford (08/12/2014) Speed distribution f ( v ) Z ∞ d R vf 1 ( v ) d σ ρ 0 = d v . d E R m χ m N d E R v min s d σ = d σ SD + d σ SI m N E R v min = 2 µ 2 d E R d E R d E R χ N Z ∞ f 1 ( v ) Mao et al., Astrophys. J. 764 (2013) 35 η ( v min ) = d v , v v min • Several theoretical models are available for f ( v ) • Standard Halo Model (SHM) is the most widely used • f ( v ) can also be derived from N -body simulations Mattia Fornasa (University of Nottingham) 2
DMUK Meeting - Oxford (08/12/2014) Determining f ( v ) with direct detection Express f(v ) in terms of a handful of parameters and, assuming data from a set of future direct detection experiments, determine them alongside m χ , σ SIp and σ SDp Polynomial parametrisation Binned parametrisation N " N − 1 # 3 g i W ( v ; ˜ v i , ∆ v ) X X f ( v ) = f ( v ) = exp a k P k (2 v/v max − 1) v i + ∆ v ) 3 − ˜ v 3 (˜ i i =1 k =0 Peter, PRD 83 (2011) 125029 m χ =30 GeV, σ SIp =10 -45 cm 2 , σ SDp =2 × 10 -40 cm 2 , S Η M Kavanagh, Fornasa & Green (arXiv:1410.8051) Mattia Fornasa (University of Nottingham) 3
DMUK Meeting - Oxford (08/12/2014) The challenge of the low-speed tail v min [km/s] Kavanagh, Fornasa & Green (arXiv:1410.8051) m χ =30 GeV, σ SIp =10 -45 cm 2 , σ SDp =2 × 10 -40 cm 2 , S Η M Mattia Fornasa (University of Nottingham) 4
DMUK Meeting - Oxford (08/12/2014) m χ =30 GeV, σ SIp =10 -45 cm 2 , σ SDp =2 × 10 -40 cm 2 , S Η M Binned parametrisation Kavanagh, Fornasa & Green (arXiv:1410.8051) Polynomial parametrisation Mattia Fornasa (University of Nottingham) 5
DMUK Meeting - Oxford (08/12/2014) m χ =100 GeV, σ SIp =10 -45 cm 2 , σ SDp =2 × 10 -40 cm 2 , S Η M Polynomial parametrisation Kavanagh, Fornasa & Green (arXiv:1410.8051) • A DM signal from neutrino telescope gives sensitivity to the low-speed tail of f ( v ) • Achieve a reconstruction of f ( v ) with an uncertainty of a factor 10 (3) for polynomial (binned) parametrisation over a range 200-300 km/s wide • Binned par. cannot be used with direct detection only (solved by IceCube data) • Polynomial par. leads to very large uncertainties (solved by IceCube data) • Flexibility of the polynomial parametrisation corresponds to more degeneracy Mattia Fornasa (University of Nottingham) 6
Recommend
More recommend