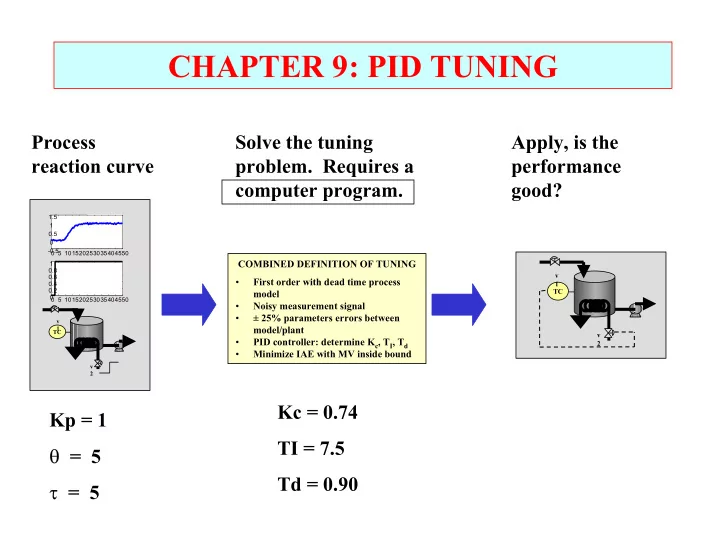
CHAPTER 9: PID TUNING Process Solve the tuning Apply, is the - PowerPoint PPT Presentation

CHAPTER 9: PID TUNING Process Solve the tuning Apply, is the reaction curve problem. Requires a performance computer program. good? 1.5 1 0.5 0 -0.5 0 5 101520253035404550 COMBINED DEFINITION OF TUNING 1 0.8 v 0.6 • First order with dead time process 0.4 1 0.2 TC model 0 0 5 101520253035404550 • Noisy measurement signal • ± 25% parameters errors between v model/plant 1 TC v • PID controller: determine K c , T I , T d 2 • Minimize IAE with MV inside bound v 2 Kc = 0.74 Kp = 1 TI = 7.5 θ = 5 Td = 0.90 τ = 5

CHAPTER 9: PID TUNING • How do we apply the same equation to many processes? • How to achieve the dynamic performance that we desire? TUNING!!!   t 1 d CV ∫ = + − + MV ( t ) K E ( t ) E ( t ' ) dt ' T I   c d T dt   I 0 The adjustable parameters are called tuning constants. We can match the values to the process to affect the dynamic performance

CHAPTER 9: PID TUNING Define the tuning Realistic situation: We will consider the PID problem controller, which is used for nearly all single- 1. Process Dynamics loop (1CV, 1MV) controllers. 2. Measured   t 1 d CV ∫ variable = + − + MV ( t ) K E ( t ) E ( t ' ) dt ' T I   c d T dt   I 0 3. Model error F S solvent 4. Input forcing F A 5. Controller pure A AC SP 6. Performance measures

CHAPTER 9: PID TUNING Define the tuning CV Dynamic Behavior: problem Stable, zero offset, minimum IAE 1. Process Dynamics 2. Measured variable MV Dynamic Behavior: damped oscillations and small fluctuations due to 3. Model error noise. 4. Input forcing MV can be more aggressive in 5. Controller early part of transient 6. Performance measures

CHAPTER 9: PID TUNING Define the tuning Our primary goal is to maintain the CV near problem the set point. Besides not wearing out 1. Process the valve, why do we have goals for the MV? Dynamics Steam flow 2. Measured 40 variable 30 Manipulated Variable 20 3. Model error 10 0 4. Input forcing -10 0 5 10 15 20 25 30 35 40 Time Large, rapid changes 5. Controller to the steam flow can AC damage the trays 6. Performance measures

CHAPTER 9: PID TUNING Define the tuning Our primary goal is to maintain the CV near problem the set point. Besides not wearing out 1. Process the valve, why do we have goals for the MV? Dynamics 2. Measured Fuel flow PI variable 1 40 AT PI 1 4 FT 30 1 TI PI 1 5 TI 5 20 TI 3. Model error 2 Manipulated Variable TI 10 6 PT 1 TI 0 3 TC TI TI 7 10 TI 4. Input forcing 4 -10 0 5 10 15 20 25 30 35 40 TI FT FI 8 TI 2 3 Time 11 Large, rapid changes PI PI PI 2 3 6 5. Controller Fuel to the fuel flow cause thermal stress that 6. Performance measures damages tubes.

CHAPTER 9: PID TUNING Define the tuning COMBINED DEFINITION OF TUNING problem PROBLEM FOR CORRELATION 1. Process Dynamics • First order with dead time process model • Noisy measurement signal 2. Measured • ± 25% parameters errors between variable model/plant • PID controller: determine K c , T I , T d 3. Model error • Minimize IAE with MV inside bound 4. Input forcing We achieve the goals by adjusting Kc, TI and Td. 5. Controller Details in chapter and Appendix E. 6. Performance measures

disturbance Set point change CHAPTER 9: PID TUNING Tuning Charts for PID Feedback Controllers These were developed by summarizing a large number of case studies in these dimensionless charts? (See page 281 in the textbook for larger plot.)

CHAPTER 9: PID TUNING Good Performance Process Solve the tuning reaction curve problem. 15 Requires a computer 10 1.5 program. CV 1 5 0.5 0 -0.5 0 5 101520253035404550 0 COMBINED DEFINITION OF TUNING 1 0.8 -5 0.6 • First order with dead time process 0 20 40 60 80 100 120 0.4 0.2 model 0 0 5 101520253035404550 • Noisy measurement signal 30 • ± 25% parameters errors between v model/plant 1 TC 20 • PID controller: determine K c , T I , T d MV • Minimize IAE with MV inside bound 10 v 2 0 0 20 40 60 80 100 120 time Kp = 1 Kc = 0.74 θ = 5 v TI = 7.5 1 TC τ = 5 Td = 0.90 v 2

CHAPTER 9: PID TUNING disturbance Set point Tuning Charts for PI Feedback Controllers These were developed by summarizing a large number of case studies in these dimensionless charts? (See page 286 in the textbook for larger plot.)

CHAPTER 9: PID TUNING Let’s apply the tuning charts to the three-tank mixing process, which is not first order with dead time. F S solvent F A pure A AC Process reaction curve Tuning from chart Kp = 0.039 %A/%open Kc = ?? θ = 5.5 min TI = ?? τ = 10.5 min Td = ??

CHAPTER 9: PID TUNING Let’s apply the tuning charts to the three-tank mixing process, which is not first order with dead time. F S solvent F A pure A AC Process reaction curve Tuning from chart Kp = 0.039 %A/%open Kc = 1.2/0.039 = 30 %open/%A θ = 5.5 min TI = 0.69(16) = 11 min τ = 10.5 min Td = 0.05(16) = 0.80 min

CHAPTER 9: PID TUNING Good Effluent concentration Concentration disturbance Performance 3.4 3.3 concentration 3.2 F S 3.1 solvent 3 0 20 40 60 80 100 120 140 160 180 200 time F A Valve % pure A open 50 AC 45 manipulated flow 40 35 30 25   t 0 20 40 60 80 100 120 140 160 180 200 1 d CV ∫ time = + − + v 30 E ( t ) E ( t ' ) dt ' 0 . 80 50   11 dt   0

CHAPTER 9: PID TUNING FINE TUNING: Process reaction curve and tuning charts provide a good method for tuning many (not all) PID loops. We need to learn how to fine tune loops to further improve performance based on current loop behavior - WHY? • Some loops could have different performance objectives • Some loops could have dynamics different from first order with dead time • Could have been error in the process reaction curve, perhaps a disturbance occurred during the experiment. • Plant dynamics can change due to changes in feed flow rate, reactor conversion, and so forth.

CHAPTER 9: PID TUNING   t 1 d CV ∫ = + − + MV ( t ) K E ( t ) E ( t ' ) dt ' T I   c d T dt   I 0 What is the effect of changing the controller gain on the control performance of a PID loop? Let’s do an experiment by changing Kc and monitoring the performance.

CHAPTER 9: PID TUNING 60 control performance, IAE • Why does IAE increase for Bad small Kc? v1 40 • Why does IAE TC ? increase for large Kc? 20 v2 0 0 0.5 1 1.5 2 controller gain 1 1 1 controlled variable controlled variable controlled variable Kc = 0.62 Kc = 1.14 Kc = 1.52 0.5 0.5 0.5 0 0 0 -0.5 -0.5 -0.5 Is this the “best”? -1 -1 -1 0 50 100 150 200 0 50 100 150 200 0 50 100 150 200 time time time PID controller with Kc changing, TI = 10, Td = 0.

CHAPTER 9: PID TUNING FINE TUNING: Let’s apply our understanding to build fine tuning guidelines. S-LOOP plots deviation variables (IAE = 9.6759) 1.5 Controlled Variable 1 This is “good” control performance. 0.5 Explain the shape of the CV and MV 0 0 5 10 15 20 25 30 35 40 responses. 45 50 Time 1.5 Manipulated Variable 1 0.5 0 0 5 10 15 20 25 30 35 40 45 50 Time

CHAPTER 9: PID TUNING Note: this is a step change to the set point - good for diagnosis! CV limited set point overshoot, fast damping, and S-LOOP plots deviation variables (IAE = 9.6759) 1.5 return to the set point Controlled Variable 1 0.5 CV does not change because of dead time 0 0 5 10 15 20 25 30 35 40 45 50 Constant slope Time E(t) = constant 1.5 Manipulated Variable MV overshoot moderate <= 0.5( ∆ MVss) 1 ∆ MV 0 = Kc ( ∆ SP) should be close to the ∆ MVss 0.5 needed change at steady state. 0 0 5 10 15 20 25 30 35 40 45 50 Time

CHAPTER 9: PID TUNING Apply the fine tuning guidelines to the response below and suggest specific changes for improvement. S-LOOP plots deviation variables (IAE = 19.3873) 1 Controlled Variable 0.8 0.6 0.4 0.2 0 0 5 10 15 20 25 30 35 40 45 50 Time 1 Manipulated Variable 0.8 0.6 0.4 0.2 0 0 5 10 15 20 25 30 35 40 45 50 Time

CHAPTER 9: PID TUNING Apply the fine tuning guidelines to the response below and suggest specific changes for improvement. S-LOOP plots deviation variables (IAE = 19.3873) 1 This is poor control Controlled Variable performance. 0.8 0.6 Controller not The CV response is very aggressive enough. 0.4 slow, not aggressive 0.2 enough Small ∆ MV 0 , increase 0 controller gain, 0 5 10 15 20 25 30 35 40 45 50 Time K c by about x2 1 Manipulated Variable 0.8 0.6 0.4 The initial change in the MV is too small, less than 40% of the final, steady-state change. 0.2 0 0 5 10 15 20 25 30 35 40 45 50 Time

CHAPTER 9: PID TUNING Apply the guidelines to the response below and suggest specific changes for improvement. S-LOOP plots deviation variables (IAE = 20.1754) 2 Controlled Variable 1.5 1 0.5 0 0 10 20 30 40 50 60 70 80 90 100 Time 2.5 Manipulated Variable 2 1.5 1 0.5 0 0 10 20 30 40 50 60 70 80 90 100 Time