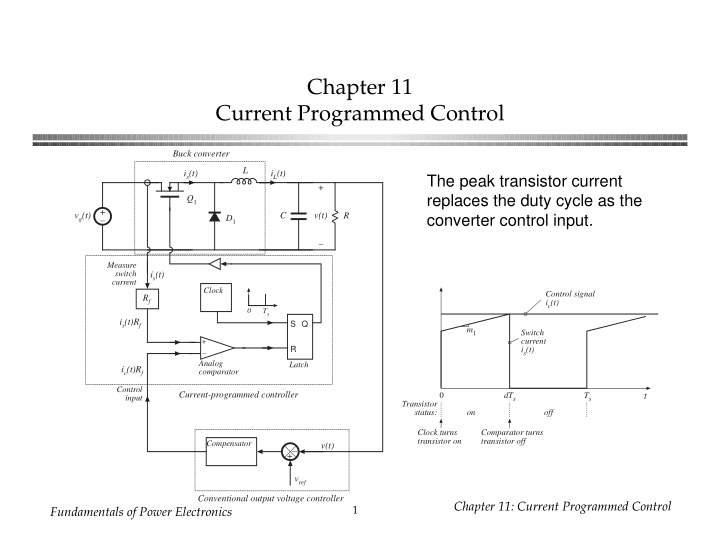
Chapter 11 Current Programmed Control Buck converter L i s (t) i L - PowerPoint PPT Presentation

Chapter 11 Current Programmed Control Buck converter L i s (t) i L (t) The peak transistor current + replaces the duty cycle as the Q 1 + v g (t) C v(t) R converter control input. D 1 – – Measure switch i s (t) current Clock Control signal R f i c (t) 0 T s i s (t)R f S Q m 1 Switch current + R i s (t) – Analog Latch i c (t)R f comparator Control Current-programmed controller 0 dT s T s t input Transistor status: on off Clock turns Comparator turns transistor on transistor off Compensator v(t) –+ v ref Conventional output voltage controller Chapter 11: Current Programmed Control 1 Fundamentals of Power Electronics

Current programmed control vs. duty cycle control Advantages of current programmed control: • Simpler dynamics —inductor pole is moved to high frequency • Simple robust output voltage control, with large phase margin, can be obtained without use of compensator lead networks • It is always necessary to sense the transistor current, to protect against overcurrent failures. We may as well use the information during normal operation, to obtain better control • Transistor failures due to excessive current can be prevented simply by limiting i c ( t ) • Transformer saturation problems in bridge or push-pull converters can be mitigated A disadvantage: susceptibility to noise Chapter 11: Current Programmed Control 2 Fundamentals of Power Electronics

Chapter 11: Outline 11.1 Oscillation for D > 0.5 11.2 A simple first-order model Simple model via algebraic approach Averaged switch modeling 11.3 A more accurate model Current programmed controller model: block diagram CPM buck converter example 11.4 Discontinuous conduction mode 11.5 Summary Chapter 11: Current Programmed Control 3 Fundamentals of Power Electronics

11.1 Oscillation for D > 0.5 • The current programmed controller is inherently unstable for D > 0.5 , regardless of the converter topology • Controller can be stabilized by addition of an artificial ramp Objectives of this section: • Stability analysis • Describe artificial ramp scheme Chapter 11: Current Programmed Control 4 Fundamentals of Power Electronics

Inductor current waveform, CCM Inductor current slopes m 1 and –m 2 i L (t) buck converter m 1 = v g – v – m 2 = – v i c L L i L (0) m 1 – m 2 i L (T s ) boost converter – m 2 = v g – v m 1 = v g L L buck–boost converter m 1 = v g – m 2 = v 0 dT s T s t L L Chapter 11: Current Programmed Control 5 Fundamentals of Power Electronics

Steady-state inductor current waveform, CPM First interval: i L (t) i L ( dT s ) = i c = i L (0) + m 1 dT s i c Solve for d : i L (0) m 1 – m 2 i L (T s ) d = i c – i L (0) m 1 T s Second interval: i L ( T s ) = i L ( dT s ) – m 2 d ' T s 0 dT s T s t = i L (0) + m 1 dT s – m 2 d ' T s In steady state: 0 = M 1 DT s – M 2 D ' T s M 2 = D D ' M 1 Chapter 11: Current Programmed Control 6 Fundamentals of Power Electronics

Perturbed inductor current waveform i L (t) i L (0) i c i L ( T s ) m 1 Steady-state waveform – m 2 I L 0 + i L (0) m 1 I L 0 – m 2 Perturbed waveform dT s 0 D + d T s DT s T s t Chapter 11: Current Programmed Control 7 Fundamentals of Power Electronics

Change in inductor current perturbation over one switching period i c magnified – m 2 i L ( T s ) i L (0) view Steady-state m 1 waveform m 1 – m 2 Perturbed dT s waveform i L (0) = – m 1 dT s i L ( T s ) = i L (0) – D i L ( T s ) = m 2 dT s D ' i L ( T s ) = i L (0) – m 2 m 1 Chapter 11: Current Programmed Control 8 Fundamentals of Power Electronics

Change in inductor current perturbation over many switching periods i L ( T s ) = i L (0) – D D ' 2 i L (2 T s ) = i L ( T s ) – D D ' = i L (0) – D D ' n i L ( nT s ) = i L (( n – 1) T s ) – D D ' = i L (0) – D D ' when – D 0 D ' < 1 i L ( nT s ) → when – D ∞ D ' > 1 D < 0.5 For stability: Chapter 11: Current Programmed Control 9 Fundamentals of Power Electronics

Example: unstable operation for D = 0.6 D ' = – 0.6 α = – D 0.4 = – 1.5 i L (t) i c 2.25 i L (0) i L (0) I L 0 – 1.5 i L (0) – 3.375 i L (0) 0 2 T s 3 T s 4 T s T s t Chapter 11: Current Programmed Control 10 Fundamentals of Power Electronics

Example: stable operation for D = 1/3 D ' = – 1/3 α = – D 2/3 = – 0.5 i L (t) i c i L (0) 1 1 16 i L (0) 4 i L (0) I L 0 – 1 – 1 2 i L (0) 8 i L (0) 0 2 T s 3 T s 4 T s T s t Chapter 11: Current Programmed Control 11 Fundamentals of Power Electronics

Stabilization via addition of an artificial ramp to the measured switch current waveform Buck converter L i s (t) i L (t) i a (t) + Q 1 + v g (t) C v(t) R D 1 m a – – 0 2 T s T s t i s (t) Measure switch R f current Now, transistor switches off Clock when i s (t)R f m a 0 T s i a (t)R f + i a ( dT s ) + i L ( dT s ) = i c + S Q Artificial ramp + or, R – Analog Latch i L ( dT s ) = i c – i a ( dT s ) i c (t)R f comparator Control Current-programmed controller input Chapter 11: Current Programmed Control 12 Fundamentals of Power Electronics

Steady state waveforms with artificial ramp i L ( dT s ) = i c – i a ( dT s ) (i c – i a (t)) i c – m a i L (t) m 1 – m 2 I L 0 0 dT s T s t Chapter 11: Current Programmed Control 13 Fundamentals of Power Electronics

Stability analysis: perturbed waveform (i c – i a (t)) i c – m a m 1 i L ( T s ) Steady-state waveform ) 0 – m 2 ( I L 0 + i L (0) i L – m 2 m 1 I L 0 Perturbed waveform dT s 0 D + d T s DT s T s t Chapter 11: Current Programmed Control 14 Fundamentals of Power Electronics

Stability analysis: change in perturbation over complete switching periods First subinterval: i L (0) = – dT s m 1 + m a Second subinterval: i L ( T s ) = – dT s m a – m 2 Net change over one switching period: i L ( T s ) = i L (0) – m 2 – m a m 1 + m a After n switching periods: i L ( nT s ) = i L (( n –1) T s ) – m 2 – m a m 1 + m a = i L (0) – m 2 – m a n = i L (0) α n m 1 + m a Characteristic value: α = – m 2 – m a when α < 1 0 i L ( nT s ) → m 1 + m a ∞ when α > 1 Chapter 11: Current Programmed Control 15 Fundamentals of Power Electronics

The characteristic value α 1 – m a m 2 α = – D + m a D ' m 2 For stability, require | α | < 1 • Buck and buck-boost converters: m 2 = – v/L • So if v is well-regulated, then m 2 is also well-regulated • A common choice: m a = 0.5 m 2 This leads to α = –1 at D = 1 , and | α | < 1 for 0 ≤ D < 1. The minimum α that leads to stability for all D . • Another common choice: m a = m 2 This leads to α = 0 for 0 ≤ D < 1. Deadbeat control, finite settling time Chapter 11: Current Programmed Control 16 Fundamentals of Power Electronics

11.2 A Simple First-Order Model Switching converter + + v g (t) v(t) R – – Converter d(t) voltages and currents Current programmed controller i c (t) v(t) Compensator +– v ref Chapter 11: Current Programmed Control 17 Fundamentals of Power Electronics

The first-order approximation i L ( t ) T s = i c ( t ) • Neglects switching ripple and artificial ramp • Yields physical insight and simple first-order model • Accurate when converter operates well into CCM (so that switching ripple is small) and when the magnitude of the artificial ramp is not too large • Resulting small-signal relation: i L ( s ) ≈ i c ( s ) Chapter 11: Current Programmed Control 18 Fundamentals of Power Electronics

11.2.1 Simple model via algebraic approach: CCM buck-boost example Q 1 D 1 + i L (t) + v g (t) L C R v(t) – – i L (t) i c v v g L L 0 dT s T s t Chapter 11: Current Programmed Control 19 Fundamentals of Power Electronics

Small-signal equations of CCM buck–boost, duty cycle control L di L ( t ) = Dv g ( t ) + D ' v ( t ) + V g – V d ( t ) dt C dv ( t ) = – D ' i L – v ( t ) R + I L d ( t ) dt i g ( t ) = Di L + I L d ( t ) Derived in Chapter 7 Chapter 11: Current Programmed Control 20 Fundamentals of Power Electronics

Transformed equations Take Laplace transform, letting initial conditions be zero: sLi L ( s ) = Dv g ( s ) + D ' v ( s ) + V g – V d ( s ) sCv ( s ) = – D ' i L ( s ) – v ( s ) R + I L d ( s ) i g ( s ) = Di L ( s ) + I L d ( s ) Chapter 11: Current Programmed Control 21 Fundamentals of Power Electronics

The simple approximation Now let i L ( s ) ≈ i c ( s ) Eliminate the duty cycle (now an intermediate variable), to express the equations using the new control input i L . The inductor equation becomes: sLi c ( s ) ≈ Dv g ( s ) + D ' v ( s ) + V g – V d ( s ) Solve for the duty cycle variations: d ( s ) = sLi c ( s ) – Dv g ( s ) – D ' v ( s ) V g – V Chapter 11: Current Programmed Control 22 Fundamentals of Power Electronics

The simple approximation, continued Substitute this expression to eliminate the duty cycle from the remaining equations: sLi c ( s ) – Dv g ( s ) – D ' v ( s ) sCv ( s ) = – D ' i c ( s ) – v ( s ) R + I L V g – V sLi c ( s ) – Dv g ( s ) – D ' v ( s ) i g ( s ) = Di c ( s ) + I L V g – V Collect terms, simplify using steady-state relations: D 2 R + 1 sCv ( s ) = sLD D ' R – D ' i c ( s ) – D R v ( s ) – D ' R v g ( s ) D 2 i g ( s ) = sLD D ' R + D i c ( s ) – D R v ( s ) – D ' R v g ( s ) Chapter 11: Current Programmed Control 23 Fundamentals of Power Electronics