1
play

1 [9-4] Mor M. Peretz, Switch-Mode Power Supplies Current feedback - PDF document

Aug 08, 2023 •143 likes •220 views

[9-1] Mor M. Peretz, Switch-Mode Power Supplies Control of switch-mode converters Current Programmed Mode control CPM Mor M. Peretz, Switch-Mode Power Supplies [9-2] Problem of voltage mode control V o d dB dB - 40 dec dB -

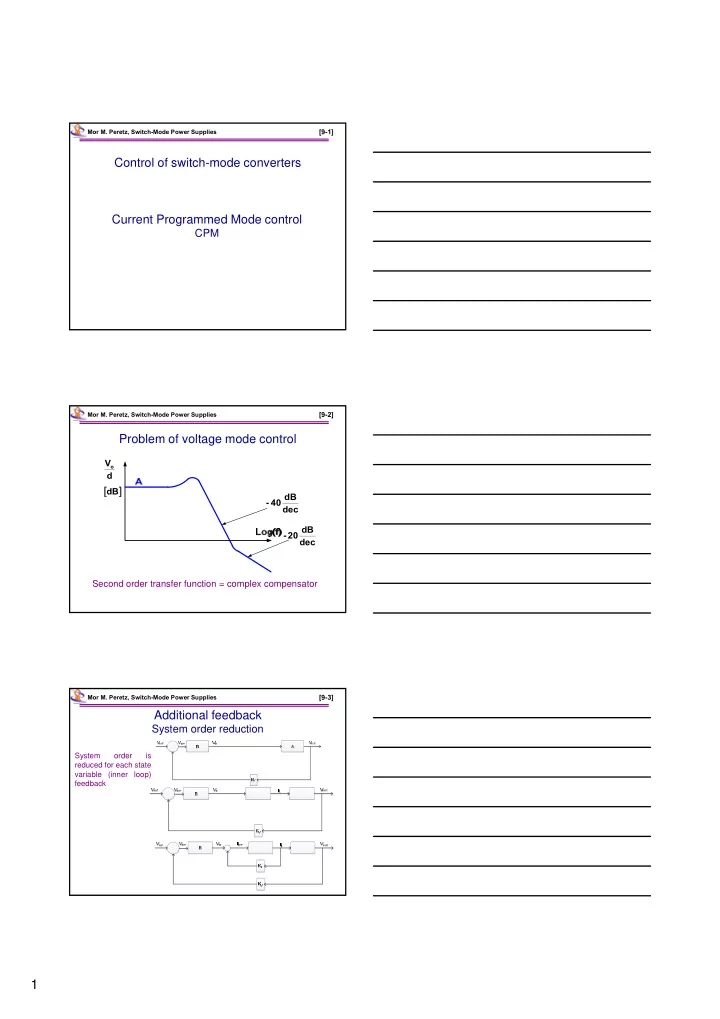
  1. [9-1] Mor M. Peretz, Switch-Mode Power Supplies Control of switch-mode converters Current Programmed Mode control CPM Mor M. Peretz, Switch-Mode Power Supplies [9-2] Problem of voltage mode control V o d   dB dB - 40 dec dB - 20 dec Second order transfer function = complex compensator Mor M. Peretz, Switch-Mode Power Supplies [9-3] Additional feedback System order reduction System order is reduced for each state variable (inner loop) feedback 1

  2. [9-4] Mor M. Peretz, Switch-Mode Power Supplies Current feedback loop I o L i o V o v o S V in C R L D N d D AMP MOD V  V v e e i o  1 For ‘strong’ feedback v N   e LG 1 v 0 ε 1  i v o e N Mor M. Peretz, Switch-Mode Power Supplies [9-5] System representation in CPM v e N v o v e R L N 1 π  2 C o R L Mor M. Peretz, Switch-Mode Power Supplies [9-6] Design of the feedback loops V o V e Instrumentation I limit L V e BW of the inner loop must be well above the outer loop BW 2

  3. [9-7] Mor M. Peretz, Switch-Mode Power Supplies Design of the feedback loops V  Mor M. Peretz, Switch-Mode Power Supplies [9-8] The advantages of current feedback v o v v o e v  20 db e dec  40 db  db dec 40 dec  db 20 dec Same power stage Typical power stage (outer loop) with VM CM Mor M. Peretz, Switch-Mode Power Supplies [9-9] Average current mode Z Z inv fv Z fi V ref 3

  4. [9-10] Mor M. Peretz, Switch-Mode Power Supplies Peak current mode I L I c t T S Cycle-by-cycle protection Mor M. Peretz, Switch-Mode Power Supplies [9-11] PCM and ACM • Current feedbacks - reduce the order of system • The difference is in BW of the current feedback loop • Increase the output impedance Mor M. Peretz, Switch-Mode Power Supplies [9-12] Sub-harmonic oscillations I L V e D<0.5  I 2 <  I 1  I 1  I 2 t T S I L V e  I D>0.5  I 2 >  I 1 1  I 2 t 4

  5. [9-13] Mor M. Peretz, Switch-Mode Power Supplies Stability analysis of Sub-harmonic oscillations       I t I m t 0 L on L 1 on       I T I t m t L s L on 2 off        I T I m t m t 0 L s L 1 on 2 off      I T I Steady-state: 0 L s L  m t m t on off 1 2 t m D   on 2 on t m D off 1 off Mor M. Peretz, Switch-Mode Power Supplies [9-14] Stability analysis of Sub-harmonic oscillations           I D  d T  I  i  m D  d T 0 0 L s L L s 1     DC I DT  I  m DT : 0 L s L s 1       AC I dT i m dT : 0 L s L s 1     i m dT 0 L s 1    i T m dT L s s 2     m D           i T i i  on  0  2  0   L s L L m D     off 1 Mor M. Peretz, Switch-Mode Power Supplies [9-15] Stability analysis of Sub-harmonic oscillations   D     i T  i   on  0   L s L D   off     2 D D               i T i T on i on 2 0     L s L s L D D     off off n     D D              i nT i n T  on  i  on  1 0     L s L s L D D     off off  D  on  0, 1  D n   D   off        i nT  Stable when D   0.5 i nT i  on  0 L s on   L s L  D D   on  off  , 1 D  off 5

  6. [9-16] Mor M. Peretz, Switch-Mode Power Supplies Slope compensation     I t  I t  I L r c       I t I I t L c r Mor M. Peretz, Switch-Mode Power Supplies [9-17] Slope compensation    I I t     c r    i m m dT 0 L r s 1        i T m m dT L r s 2    m m       i T i  2 r  0 L s L  m m   n    r m m 1           n i nT i  r  i 0 2 0 L s L  L m m   r 1     0, 1     i nT L s    , 1  m m   r r 1 1  m m m m m          r r 2 2 2 0.5  m m D m m m m   r on r r 1 1 2 m m D m off 2 2 2 Mor M. Peretz, Switch-Mode Power Supplies [9-18] 6

  7. [9-19] Mor M. Peretz, Switch-Mode Power Supplies Mor M. Peretz, Switch-Mode Power Supplies [5-20] 7

Recommend

More recommend