Can you put the balls in boxes so that no box has more than one - PowerPoint PPT Presentation

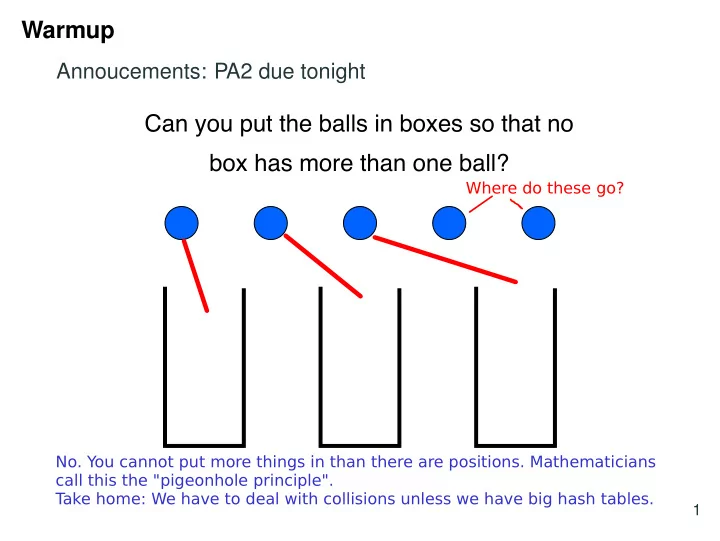
Warmup Annoucements: PA2 due tonight Can you put the balls in boxes so that no box has more than one ball? Where do these go? No. You cannot put more things in than there are positions. Mathematicians call this the "pigeonhole principle". T ake home: We have to deal with collisions unless we have big hash tables. 1

Collisions A collision occurs when two keys map to the same place, that is for x , y ∈ K with x � y we have hash ( x ) = hash ( y ) . K is the set of keys Hash table Collision Keys 1 201 Will Geoff 3 202 Cinda Andy/Cinda Hash function m-1 203 We will use m to denote the size of the hash table 2 We will use n or k to denote the number of keys

What is the probability a collision happens? What is the probability someone in this room has a birthday Assume 365 days in a year. today? 364 Prob of one person not having bday today 365 � k � 364 Prob of k people not having bday 365 � k � 364 Prob of someone having bday today 1 − 365 What is the probability two people in this room share the same With one person p=0 With 366 p=1 by pigeonhole birthday? 1 Intuitive but wrong p= (k -1) / 365 365 · 364 365 365 · · · 365 − ( k − 1) Prob k people not sharing 365 0.5 p Prob of sharing = 1 - 23 366 1 k 3

Expected value De fi nition: The expected value of a (discrete) random variable X is: You could think of this as the average value � E [ X ] = x · Prob ( X = x ) x ∈ X where X is the set of values X could have. Question: Suppose we role a fair six sided die, that is all value are equally probable. What is the expected value? E [ X ] = 1 · 1 6 + 2 · 1 6 · · · 6 · 1 6 = 3 . 5 Remember this is like an average. You don't really expect a single roll of the die to show 3.5. But if you do a bunch and average then the value you get would be close to 3.5. 4

Linearity of expected value For any two random variables X and Y we have E [ X + Y ] = E [ X ] + E [ Y ] . Example: Rolling two six side dice. What is the expected value of the sum of the dice? Slow way: T wo ways to get 3 2 · 1 36 + 3 · 2 36 + · · · 12 · 1 1 2 3 4 5 6 36 = 7 1 2 3 4 5 6 7 2 3 4 5 6 7 8 36 possibilities 3 4 5 6 7 8 9 Better way: 4 5 6 7 8 9 10 E[X+Y] = E[X] + E[Y] = 3.5 + 3.5 = 7 5 6 7 8 9 10 11 We use that E[X]=E[Y]=3.5 from last slide 6 7 8 9 10 11 12 because we have fair dice. This holds for any two random variables even if they are NOT independent. 5

How many collisions should we expect? What is the expected number of people who share a birthday in the room?  Indicator variable    1 if person i and j share a birthday Let X i j =  0 otherwise   Then � n � n j = i + 1 X i j is the number of people who share i = 1 birthdays. E [ � n � n j = i + 1 X i j ] = � n � n j = i + 1 E [ X i j ] = � n � n Prob( X ij = 1) i = 1 i = 1 i = 1 j = i + 1 n n 365 = n ( n − 1) 1 1 1 � � = · 2 365 365 i =1 j = i +1 First person picks any day, then second can only pick the same day 1 out of 365 ways. Generalisation and collisions: If we randomly put k items into m bins k ( k − 1 ) we expect 1 pairs to collide (share the same bin). To have one m 2 √ k ( k − 1 ) or more expected collisions we solve 1 ≥ 1 = ⇒ k � 2 m . m 2 T ake home: We expect collisions even with few keys. Example: If m=10,000 then with about 140 keys we expect a collision. 6

Building a hash function Conceptually there are two challenges: 1. Mapping our keys to integers 2. Mapping the resulting integers to array indices { 1 , 2 , 3 ,..., m − 1 } Step 2 0 42 Step 1 1 201 Geoff 2 1023 Cinda 3 203 Andy/Cinda 100003234 4 202 5 Later we will pretend like our keys are integers but they could be anything we just assume we 6 know how to do step 1. In practice we typically solve them together 7

ASCII Code Mapping strings to integers A=65, n=110, d=100, y=121 How do we map “Andy” to a number? 256 3 · + 256 2 · + 256 1 · + 256 0 · = 2036624961 100 110 65 121 Is this a good mapping scheme? What if the string is long? GOT book ~ 6,000,000 chars Human genome ~ 3,000,000,000 chars We would over fl ow very quickly with these strings Solution: We can use mod to wrap the values back 8

Evaluate from inside out Horners rule Hashing strings x 3 + x 2 + x = x ( x 2 + x + 1) = x ( x ( x + 1) + 1) int hash( string s, int p ) { int h = 0; for (i = s.length() - 1; i >= 0; i--) { h = (256 * h + s[i]) % p; Wrapping values to avoid over fl ow } (a+b) mod c = a mod c + b mod c Collision return h; } hash("Andy", 1024) = 577 hash("Andy/Cinda", 1024)=577 hash("Cinda", 1024) = 323 hash("Geo ff ", 1024) = 327 Runtime: Θ ( s ) What is the right parameter for runtime? Length of string = s This could be bad if we hash a human genome Solution: When building the hash function pick a random set of positions and only hash those. 9

Fixed hash functions are a bad idea Always using the same hash function can lead to poor performance: • If a malicious user knows your hash function they can always cause a collision • Even a nice user could cause problems. Suppose we use the previous hash function and set p = 65, note this is the ASCII value for “A”. Then what does the following code do? 0 cout << hash("A", 65); cout << hash("AA", 65); 0 cout << hash("AAA", 65); 0 0 cout << hash("AAAA", 65); The solution is to create a new hash function everytime you create a dictionary. For the current example this could mean choosing a random value of p . 10

Universal hashing De fi nition: A set H of hash functions is universal if for all x � y , the probability that hash ( x ) = hash ( y ) is at most 1 m when hash() is chosen at random from H . Note: hash is random, x and y are fi xed Example: Let p be a prime number larger than any key. Choose a at random from { 1 , 2 ,..., p − 1 } and b at random from { 0 , 1 ,..., p − 1 } the following set of functions is universal h ( x ) (( a · x + b ) mod p ) mod m = Squish values into array Why should p be prime and bigger than the keys? Then p is not divisible by x. Same argument for picking a and b. Why can't a be 0? Every value maps to the same place! 11

Collisions and hash function summary • We can only avoid collisions if the size of the set of all possible keys we want to hash is less than equal to the size of our hash table and we have a perfect hash function • This is bad if the set of keys is in fi nitely large • This is still bad if the set of keys is very big as it will require a big hash table and lots of memory • We have to deal with collisions • Even with ≈ √ m keys we will expect to have a collision • We need a collision resolution strategy • Separate chaining • Open addressing • Many other interesting strategies we won’t talk about 12