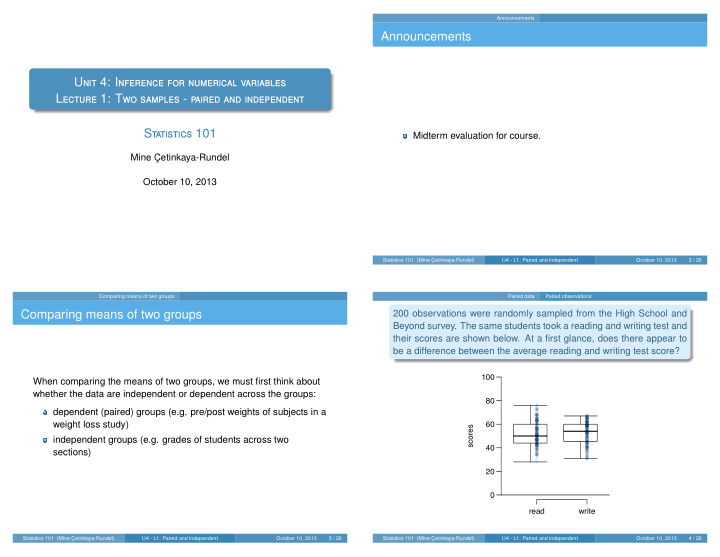
Announcements U nit 4: I nference for numerical variables L ecture 1: - PowerPoint PPT Presentation

Announcements Announcements U nit 4: I nference for numerical variables L ecture 1: T wo samples - paired and independent S tatistics 101 Midterm evaluation for course. Mine C ¸ etinkaya-Rundel October 10, 2013 Statistics 101 (Mine C ¸ etinkaya-Rundel) U4 - L1: Paired and independent October 10, 2013 2 / 26 Comparing means of two groups Paired data Paired observations Comparing means of two groups 200 observations were randomly sampled from the High School and Beyond survey. The same students took a reading and writing test and their scores are shown below. At a first glance, does there appear to be a difference between the average reading and writing test score? 100 When comparing the means of two groups, we must first think about whether the data are independent or dependent across the groups: 80 dependent (paired) groups (e.g. pre/post weights of subjects in a weight loss study) 60 scores independent groups (e.g. grades of students across two 40 sections) 20 0 read write Statistics 101 (Mine C ¸ etinkaya-Rundel) U4 - L1: Paired and independent October 10, 2013 3 / 26 Statistics 101 (Mine C ¸ etinkaya-Rundel) U4 - L1: Paired and independent October 10, 2013 4 / 26

Paired data Paired observations Paired data Paired observations Analyzing paired data Clicker question When two sets of observations have this special correspondence The same students took a reading and writing test and their scores are (not independent), they are said to be paired . shown below. Are the reading and writing scores of a given student To analyze paired data, it is often useful to look at the difference independent of each other? in outcomes of each pair of observations. diff = read − write id read write 1 70 57 52 It is important that we always subtract using a consistent order. 2 86 44 33 40 3 141 63 44 4 172 47 52 id read write diff 30 . . . . Frequency . . . . 1 70 57 52 5 . . . . 20 2 86 44 33 11 200 137 63 65 3 141 63 44 19 10 4 172 47 52 -5 (a) Yes (b) No . . . . . . . . . . 0 . . . . . −20 −10 0 10 20 200 137 63 65 -2 differences Statistics 101 (Mine C ¸ etinkaya-Rundel) U4 - L1: Paired and independent October 10, 2013 5 / 26 Statistics 101 (Mine C ¸ etinkaya-Rundel) U4 - L1: Paired and independent October 10, 2013 6 / 26 Paired data Paired observations Paired data Inference for paired data Parameter and point estimate Setting the hypotheses If in fact there was no difference between the scores on the reading and writing exams, what would you expect the average difference to Parameter of interest: Average difference between the reading be? and writing scores of all high school students. What are the hypotheses for testing if there is a difference between the µ diff average reading and writing scores? H 0 : There is no difference between the average reading and writing Point estimate: Average difference between the reading and score. writing scores of sampled high school students. µ diff = 0 ¯ x diff H A : There is a difference between the average reading and writing score. µ diff � 0 Statistics 101 (Mine C ¸ etinkaya-Rundel) U4 - L1: Paired and independent October 10, 2013 7 / 26 Statistics 101 (Mine C ¸ etinkaya-Rundel) U4 - L1: Paired and independent October 10, 2013 8 / 26

Paired data Inference for paired data Paired data Inference for paired data Nothing new here Checking assumptions & conditions Clicker question Which of the following is true? (a) Since students are sampled randomly and are less than 10% of all high school students, we can assume that the difference The analysis is no different than what we have done before. between the reading and writing scores of one student in the We have data from one sample: differences. sample is independent of another. We are testing to see if the average difference is different than 0. (b) The distribution of differences is bimodal, therefore we cannot continue with the hypothesis test. (c) In order for differences to be random we should have sampled with replacement. (d) Since students are sampled randomly and are less than 10% all students, we can assume that the sampling distribution of the average difference will be nearly normal. Statistics 101 (Mine C ¸ etinkaya-Rundel) U4 - L1: Paired and independent October 10, 2013 9 / 26 Statistics 101 (Mine C ¸ etinkaya-Rundel) U4 - L1: Paired and independent October 10, 2013 10 / 26 Paired data Inference for paired data Paired data Inference for paired data Application exercise: HT ↔ CI Work in teams: The observed average difference between the two scores is -0.545 points and the standard deviation of the difference is 8.887 points. Which of the below is the closest p-value for evaluating a difference between the average scores on the two exams? In addition, write out the interpretation Clicker question of the p-value in context of the data and the research question. Suppose we were to construct a 95% confidence interval for the av- erage difference between the reading and writing scores. Would you (a) 20% (c) 5% (e) 95% (b) 40% expect this interval to include 0? (d) 48% (a) yes (b) no (c) cannot tell from the information given Statistics 101 (Mine C ¸ etinkaya-Rundel) U4 - L1: Paired and independent October 10, 2013 11 / 26 Statistics 101 (Mine C ¸ etinkaya-Rundel) U4 - L1: Paired and independent October 10, 2013 12 / 26

Difference of two means Confidence intervals for differences of means Difference of two means Confidence intervals for differences of means Exploratory analysis The General Social Survey (GSS) conducted by the Census Bureau contains a standard ‘core’ of demographic, behavioral, and attitudinal What can you say about the relationship between educational attain- questions, plus topics of special interest. Many of the core questions ment and hours worked per week? have remained unchanged since 1972 to facilitate time-trend studies as well as replication of earlier findings. Below is an excerpt from the 2010 data set. The variables are number of hours worked per week ● ● ● ● ● ● ● ● ● ● ● ● 80 and highest educational attainment. ● ● ● ● ● ● ● ● ● ● ● ● 60 degree hrs1 40 1 BACHELOR 55 2 BACHELOR 45 ● 3 JUNIOR COLLEGE 45 20 ● ● ● ● ● ● ● ● ● ● . ● ● . ● ● ● ● ● ● ● ● ● ● ● . ● ● ● ● ● ● ● ● ● ● ● ● ● 0 1172 HIGH SCHOOL 40 Less than HS HS Jr Coll Bachelor's Graduate Statistics 101 (Mine C ¸ etinkaya-Rundel) U4 - L1: Paired and independent October 10, 2013 13 / 26 Statistics 101 (Mine C ¸ etinkaya-Rundel) U4 - L1: Paired and independent October 10, 2013 14 / 26 Difference of two means Confidence intervals for differences of means Difference of two means Confidence intervals for differences of means Collapsing levels into two Using R: Construct new variable gss = read.csv("http://stat.duke.edu/courses/Summer13/ sta104.01-1/resources/data/gss.csv") # create a new empty variable Say we are only interested the difference between the number of gss$edu = NA hours worked per week by college and non-college graduates. # if statements to determine levels of new variable Then we combine the levels of education into two: gss$edu[gss$degree == "LESS THAN HIGH SCHOOL" | hs or lower ← less than high school or high school gss$degree == "HIGH SCHOOL"] = "hs or lower" coll or higher ← junior college, bachelor’s, and graduate gss$edu[gss$degree == "JUNIOR COLLEGE" | gss$degree == "BACHELOR" | gss$degree == "GRADUATE"] = "coll or higher" # make sure new variable is categorical gss$edu = as.factor(gss$edu) Statistics 101 (Mine C ¸ etinkaya-Rundel) U4 - L1: Paired and independent October 10, 2013 15 / 26 Statistics 101 (Mine C ¸ etinkaya-Rundel) U4 - L1: Paired and independent October 10, 2013 16 / 26