Alpha decay Alpha Decay Alpha Decay Energy relations S ( A , Z ) = - PowerPoint PPT Presentation

Alpha decay

Alpha Decay

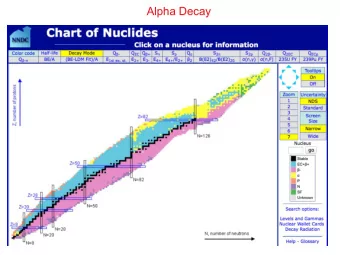
Alpha Decay Energy relations S α ( A , Z ) = − Q α ( A , Z ) = B ( A , Z ) − B ( A − 4, Z − 2) − 28.3MeV Q α = T α + T d = experimental binding # & # & energy of 4 He M D + M α A % ( T α ( ≈ T α % ( % $ ' M D A − 4 $ ' +electron screening recoil term effect +bremsstrahlung http://www.nndc.bnl.gov/chart/reColor.jsp?newColor=qa

Theory of Alpha decay: Gamow 1928 Coulomb potential Attractive nuclear potential At t =0, alpha particle is localized inside the nucleus. It can be represented by a wave packet. At large times, the wave function is an outgoing wave.

Two potential approach to tunneling (decay width and shift of an isolated quasistationary state) Phys. Rev. A 38, 1747 (1988); Phys. Rev. A69, 042705 (2004) Fermi’s golden rule! ( ) = U r ( ) + W r ( ) V r open closed scattering ˜ W = W + V 0

2 $ ' r P = χ III 2 T ∝ 1 ∫ 2 ∝ exp − 2 k ( r ) dr & ) & ) χ I P % ( r 1 In the case of the Coulomb barrier, the above integral can be evaluated exactly. b log T = a + Q α Geiger-Nuttall law of alpha decay 1911 For the Coulomb barrier above, derive the Geiger-Nuttal law. Assume that the energy of an alpha particle is E=Q α , and that the outer turning point is much greater than the potential radius.

Phys. Lett. B 734 203 (2014) (a) Pb 10 9 Po 10 6 Rn 1/2 [sec] 10 3 Ra T 10 0 Yb 186 Po Hf 10 -3 W Hg Pt Os T 1/2 (exp)/T 1/2 (GN) 10 -6 186 Po 186-208 Po 10 g.s.->g.s. decays 190 Po 188 Po 1 (b) 0,1 0,34 0,36 0,38 0,40 0,42 0,44 0,46 Q a -1/2