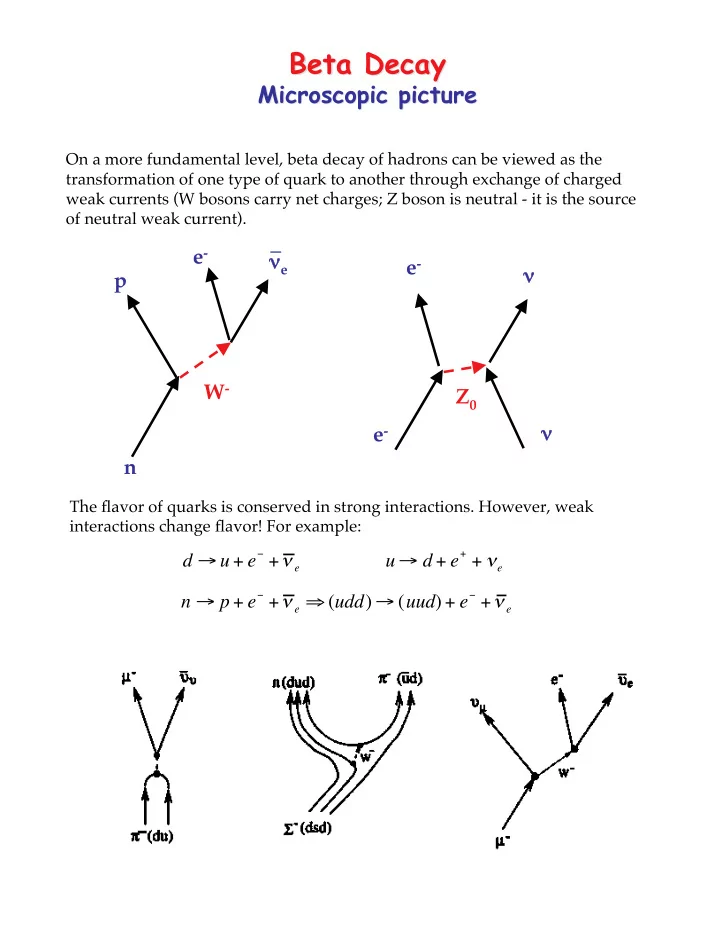

Beta Decay Beta Decay Microscopic picture Microscopic picture On a more fundamental level, beta decay of hadrons can be viewed as the transformation of one type of quark to another through exchange of charged weak currents (W bosons carry net charges; Z boson is neutral - it is the source of neutral weak current). _ e - ν e e - ν p W - Z 0 e - ν n The flavor of quarks is conserved in strong interactions. However, weak interactions change flavor! For example: � + � e + + � e d � u + e u � d + e � + � e � ( udd ) � ( uud ) + e � + � e n � p + e
Beta Decay Beta Decay Microscopic picture Microscopic picture When a quark decays, the new quark does not have a definite flavor. For instance: Cabibbo angle u � d ' = d cos � c + s sin � c However, the observed weak transitions are between quarks of definite flavor. The strong-interaction quark eigenstates � � � � � � u c t � � � � � � � � � � � � d s b � � � � � � are different from weak interaction eigenstates). � � � � � � u c t � � � � � � � � � � � � d ' s ' b ' � � � � � � This means that the observed beta-decay strength in reactions is modified by the mixing angle. � � � � � � d ' U ud U us U ub d Cabibbo _Kobayashi- � � � � � � s ' U cd U cs U cb s � � = � � � � Maskawa (CKM) matrix � � � � � � b ' U td U ts U tb b � � � � � � For nuclear beta-decay, we are mainly concerned with the transition between u- and d-quarks. As a result, only the product G V = G F cos � c enters into the process.
Beta Decay Beta Decay Microscopic picture Microscopic picture What are the consequences of parity violation in beta decay? � � r r p helicity h = p The eigenvalue of h is v/c . For a massless particle, the eigenvalues of h can be only +1 or -1. In general, the particle with • h>0 is called “right-handed” • h <0 is called “left-handed” Experimentally, ± ) = m v/ c h ( � e ) � � 1 , h ( � e ) � + 1 , h ( e All the leptons emitted in beta-decays are left-handed and all antileptons - right-handed! The operators that are scalars, pseudoscalars and tensors produce leptons of both helicities under a parity transformation. Only vector operators V and axial vector operators A can accommodate the observed result. Furthermore, since V and A are of different parity, they must appear in a linear combination. This leads to the V-A theory of beta decay. In principle, both V and A parts should be characterized by different coupling constants, G V and G A , respectively. The vector current is known to be a conserved quantity (CVC hypothesis) four-divergence V � , � = 0 For the axial vector current, there is not such a relation. The four-divergence of A (a pseudoscalar!) does not vanish. The pion is a pseudoscalar particle. Hence the weak interaction is modified in the presence of strong interactions. This leads to a partially conserved axial-vector current (PCAC) hypothesis: A � , � = a � � a constant the pion field
Beta Decay Beta Decay Microscopic picture (cont.) Microscopic picture (cont.) How to relate G V and G A ? pion decay constant pion-nucleon coupling constant g A � G A = f � g � n Goldberger-Trieman relation 2 G V M N c Experimentally, g A =-1.259 This value is close to obtained from the relation above. It is a nice g A � 1.31 confirmation of the PCAC Matrix elements Matrix elements V int � g � r n � r ) � r n � r ) � r n � r ( ) ˆ ( zero-range ( r r r r r r O ( n � p ) p e � � The nuclear operator transforming a neutron into a proton must be one body in nature. Hence it must involve the isospin raising or lowering operators. In the non-relativistic limit, the vector part may be represented by the unity � ± � ± operator times and the axial-vector part by a product of and σ . (A proper derivation requires manipulation with Dirac 4-component fuctions and γ matrices!) Gamow-Teller decay, carries one unit of angular momentum A r ( j ) � r � [ ] V int � G V � ± ( j ) + g A � ( j ) � j = 1 Fermi decay, carries zero angular momentum
Beta Decay Beta Decay Allowed decays Allowed decays Fermi transitions Fermi transitions J f M f T f T 0 f T m J i M i T i T 0 i = T i ( T i + 1) � T 0 i ( T 0 i m 1) � J i J f � M i M f � T i T f � T 0 i m 1 T 0 f In reality, isospin is violated by the electromagnetic force, but the violation is weak. ( ) J f = J i � J = 0 T + has rank ( ) T f = T i � 0 � T = 0, but T i = 0 � T f = 0 forbidden unity! T 0 f = T 0 i m 1 ( ) � T 0 = 1 � � = 0 no parity change Gamow-Teller transitions -Teller transitions Gamow The matrix element strongly depends on the structure of the wave function! � J = 0,1 but J i = 0 � J f = 0 forbidden � T = 0,1 but T i = 0 � T f = 0 forbidden ( ) T 0 f = T 0 i m 1 � T 0 = 1 � � = 0 no parity change The absolute values of GT matrix elements are generally smaller than those for Fermi transitions. const fT = 2 + g A 2 GT 2 F squared matrix elements
Beta Decay Beta Decay Forbidden transitions Forbidden transitions Forbidden transitions involve parity change and a spin change of more than one unit. They come from the higher-order terms in the expansion of electron and neutrino plane waves into spherical harmonics. Forbidden decays are classified into different groups by the L -value of the spherical harmonics involved. The selection rules for the L th-order forbidden transitions are: L � J = L or L ± 1, � � = ( � 1) Experimental log fT values
Beta Decay Beta Decay electron capture processes electron capture processes Electron capture leads to a vacancy being created in one of the strongest bound atomic states, and secondary processes are observed such as the emission of X- rays and Auger electrons. Auger electrons are electrons emitted from one of the outer electron shells and take away some of the remaining energy. Capture is most likely for a 1s-state electron. The K-electron wave function at the origin is maximal and is given by 3/2 � � Zm e e 2 � e � (0) = 1 � � � � 2 h � � � The electron capture probability is thus given by: 2 g 3 ' 2 � � 2 M fi Zm e e 2 W � � EC = E v � � 2 h 4 c 3 2 h � � �
Recommend
More recommend