3d viewing as a Kodak moment Projection 3D viewing is much like - PDF document

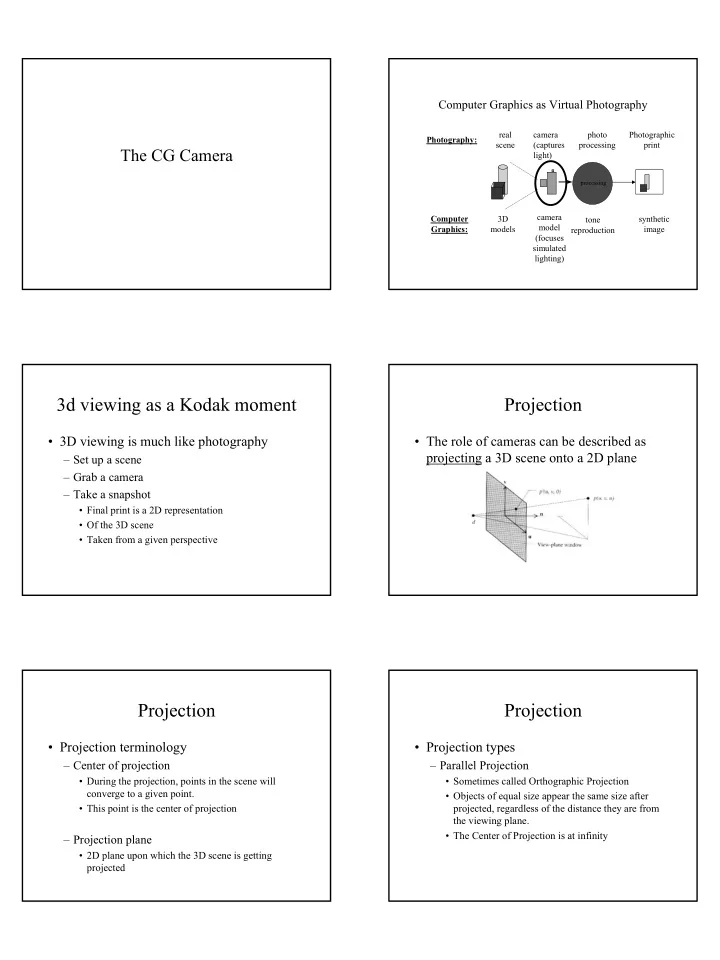
Computer Graphics as Virtual Photography real camera photo Photographic Photography: scene (captures processing print The CG Camera light) processing camera Computer 3D synthetic tone model Graphics: models reproduction image (focuses simulated lighting) 3d viewing as a Kodak moment Projection • 3D viewing is much like photography • The role of cameras can be described as projecting a 3D scene onto a 2D plane – Set up a scene – Grab a camera – Take a snapshot • Final print is a 2D representation • Of the 3D scene • Taken from a given perspective Projection Projection • Projection terminology • Projection types – Center of projection – Parallel Projection • During the projection, points in the scene will • Sometimes called Orthographic Projection converge to a given point. • Objects of equal size appear the same size after • This point is the center of projection projected, regardless of the distance they are from the viewing plane. • The Center of Projection is at infinity – Projection plane • 2D plane upon which the 3D scene is getting projected

Projection Projection • Parallel Projection • Projection types – Perspective Projection • Sometimes called Frustrum Projection Center of • Objects closer to the view plane will appear larger projection when projected than objects of the same size that are at infinity farther from the view point. Object in • The Center of Projection is at camera location View plane (eyepoint) 3D scene • This is the projection used by “real” cameras Projection Projection • Perspective Projection • Perspective • Parallel Cameras in Computer Graphics View Volumes • Just like in photography, – Your camera will define what part of the scene you can see. – Based on: • Projection type used by camera • Location of camera • Direction of camera • Orientation of camera • “Range” of your camera – All of the above will define a view volume • All objects in the view volume are seen by the camera

Camera Coordinates Camera coordinates • Defining camera orientation • Camera Orientation – Provide the camera location (eyepoint) – The camera has it’s own 3D coordinate system – Indicate what direction the camera is looking based on it’s orientation (lookat) • u,v,n – Give the “up” direction of the camera • u corresponds to x (as seen by the camera) – Then • v corresponds to y (as seen by the camera) • n = eyepoint – lookat • n corresponds to z (as seen by the camera) • u = up x n – Negative n is into the scene • v = n x u View Volumes View Volumes • Also needed to define the view volumes • Let’s see all this in action! – Location of the near and far clipping planes – This will give you the “range” of the camera Projection Projection • View coordinate system may not coincide • (u x ,u y ,u z ) are coordinates with world coordinate system. of unit u vector w.r.t.  −  u u u o x y z x world space   • Must transform point in world (x,y,z) to a − v v v o   • Similar for v, n, = x y z y M point in coordinate system of view (u,v,n)  −  n n n o • (o x , o y , o z ) is the origin x y z z       u x 0 0 0 1 of view space w.r.t world       space v y     = M     n z     1 1    

Projection Projection ′ p p = u u • Now that you’re in u,v,n space, you still + d p d n need to perform the perspective projection. p ′ = p u u p + 1 n d ′ p p = v v + d p d n p ′ = p v v p + 1 n d Projection Projection • Recall homogeneous coordinates • In Matrix form: – (X,Y,Z,W) where x = X/W, y = Y/W, z = Z/W  P   1 0 0 0   u   u  u         P 0 1 0 0 v v         v = = P p p p p         ′ ′ = u = u = v = v P 0 0 1 0 n n p p u p v p n W W         + + 1 1 n n d d W 0 0 1 d 1 1 1         p = d + n W 1 Projection Camera Coordinates • Combine with your coordinate system • The coordinates of the objects in the 3D transform scene must be converted to the coordinate     P p system of the camera u x     • In fact, the whole image generation process P p     v = y PM is nothing more than a series of     P p concatenated transformations n z     w 1    

Homogeneous Matrices Graphics Pipeline  x   p p p p   m m m m   x  v 11 12 13 14 11 12 13 14 o         y p p p p m m m m y         v = 21 22 23 24 ⋅ 21 22 23 24 ⋅ o         z p p p p m m m m z v 31 32 33 34 31 32 33 34 o         1 p p p p m m m m 1         { 41 42 43 44 41 42 43 44 { 1 4 4 4 4 2 4 4 4 4 3 1 4 4 4 4 2 4 4 4 4 3 view plane projection world to camera object Projection The Pinhole Camera • And this is how it’s done in computer • CG uses the pinhole camera model graphics • Use homogeneous coordinates to include perspective transformation in matrix transform chain. • So how does all this relate to real cameras... The Pinhole Camera Depth of field • However – Real cameras have real openings (apertures) -- depth of field – Shutter speed is not instantaneous -- motion blur – Projection is not necessarily perfectly perspective – lens warping

Motion blur Realistic Lens models 35mm wide-angle 200mm telephoto 50mm double-Gauss 16mm fisheye Realistic Camera Models Remember • We will talk more about more accurately • Project proposals due in 1 week modeling “real” camera during our discussion of Tone Reproduction • Class Web Site: – http://www.cs.rit.edu/~jmg/cgII • Questions?