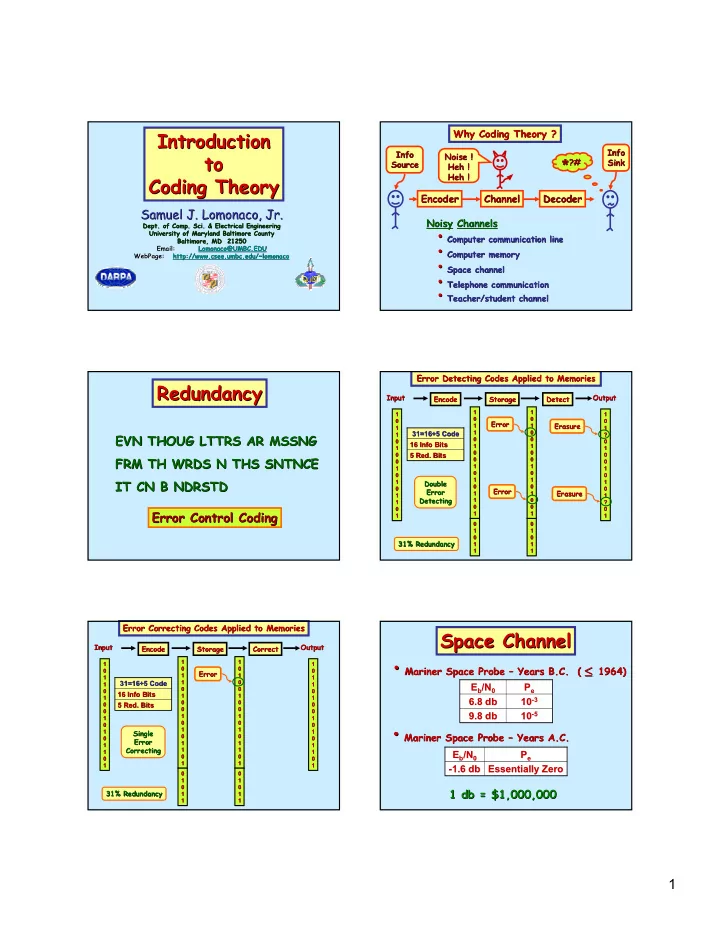

Introduction Why Coding Theory ? Why Coding Theory ? Introduction Info Info Info Info to to Noise ! Noise ! � ?# ?# Sink Sink Source Source � Heh ! Heh ! Heh ! Heh ! Coding Theory Coding Theory Encoder Encoder Channel Channel Decoder Decoder Samuel J. Lomonaco, Jr. Samuel J. Lomonaco, Jr. Noisy Channels Noisy Channels Dept. of Comp. Sci. & Electrical Engineering Dept. of Comp. Sci. & Electrical Engineering • Computer communication line • University of Maryland Baltimore County University of Maryland Baltimore County Computer communication line Baltimore, MD 21250 Baltimore, MD 21250 • Computer memory • Email: Email: Lomonaco@UMBC.EDU Lomonaco@UMBC.EDU Computer memory WebPage: http://www.csee.umbc.edu/~lomonaco WebPage: http://www.csee.umbc.edu/~lomonaco • Space channel • Space channel • Telephone communication • Telephone communication • • Teacher/student channel Teacher/student channel Error Detecting Codes Applied to Memories Error Detecting Codes Applied to Memories Redundancy Redundancy Input Input Output Output Encode Storage Detect Encode Storage Detect 1 1 1 1 1 1 1 1 0 0 0 0 0 0 Error Error 0 0 Erasure Erasure 1 1 1 1 1 1 1 1 1 1 0 0 EVN THOUG LTTRS AR MSSNG 31=16+5 Code 31=16+5 Code EVN THOUG LTTRS AR MSSNG 1 1 ? ? 0 0 0 0 0 0 0 0 16 Info Bits 16 Info Bits 1 1 1 1 1 1 1 1 0 0 0 0 0 0 5 Red. Bits 0 0 5 Red. Bits FRM TH WRDS N THS SNTNCE FRM TH WRDS N THS SNTNCE 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 IT CN B NDRSTD IT CN B NDRSTD 1 1 Double Double 1 1 1 1 1 1 0 0 0 0 0 0 Error Error Error 0 0 Error Erasure Erasure 1 1 1 1 1 1 1 1 Detecting Detecting 1 1 0 0 1 ? 1 ? 0 0 0 0 0 0 0 0 Error Control Coding Error Control Coding 1 1 1 1 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 31% Redundancy 31% Redundancy 1 1 1 1 1 1 1 1 Error Correcting Codes Applied to Memories Error Correcting Codes Applied to Memories Space Channel Space Channel Input Input Output Output Encode Encode Storage Storage Correct Correct • Mariner Space Probe • 1 1 1 1 1 1 1 1 ≤ ≤ Mariner Space Probe – – Years B.C. ( 1964) Years B.C. ( 1964) 0 0 0 0 0 0 Error Error 0 0 1 1 1 1 1 1 1 1 31=16+5 Code 31=16+5 Code 1 1 0 0 1 1 1 1 E b /N 0 P e E b /N P 0 0 0 0 0 e 0 0 0 0 16 Info Bits 16 Info Bits 1 1 1 1 1 1 1 1 10 - -3 3 6.8 db 6.8 db 10 0 0 0 0 0 0 0 5 Red. Bits 5 Red. Bits 0 0 0 0 0 0 0 0 0 10 - -5 5 9.8 db 9.8 db 10 1 1 1 1 1 1 1 1 • Mariner Space Probe • 0 0 0 0 0 0 0 0 Single 1 1 1 1 Single 1 1 1 1 Mariner Space Probe – – Years A.C. Years A.C. 0 0 0 0 0 0 0 0 Error Error 1 1 1 1 1 1 1 1 Correcting Correcting 1 1 1 1 1 1 1 1 E b E b /N /N 0 P P e 0 0 0 0 0 0 0 e 0 0 1 1 1 1 1 1 1 1 - -1.6 db 1.6 db Essentially Zero Essentially Zero 0 0 0 0 1 1 1 1 0 0 0 0 1 db = $1,000,000 1 db = $1,000,000 31% Redundancy 31% Redundancy 1 1 1 1 1 1 1 1 1
Types of Channels Types of Channels 2 2- -Repeat Code Repeat Code − 1 p 0 0 Info. Words Info. Words Code Words Code Words p 0 0 00 00 p 1 1 1 1 11 11 − 1 p Detects all single errors Detects all single errors Binary Symmetric Channel (BSC) Binary Symmetric Channel (BSC) If we use If we use BEC BEC with with probability of transition probability of transition p = 10 p = 10 - -2 2 , , then the probability probability P P U of undetectable error is Erasure then the U of undetectable error is Erasure − 1 p 0 0 = = = = − 2 4 10 P p p ? U Moreover, Moreover, p 1 1 # Info Bits 1 − = = = = = 1 p Rate R Binary Erasure Channel (BEC) Binary Erasure Channel (BEC) # 2 All Bits Shannon’ Shannon ’s Theorem s Theorem A Surprise in Communication Theory A Surprise in Communication Theory 1 Repetition Repetition Prob. Of Msg. Error Prob. Of Msg. Error 10 − 2 Coding Coding Within a large class of coding schemes Within a large class of coding schemes 10 − 4 there exist some schemes – there exist some schemes – nearly all, nearly all, 10 − 6 Limit Given Limit Given actually – actually – that give arbitrarily low error that give arbitrarily low error 10 − 8 by Shannon’ by Shannon ’s s rates at any information rate up to a rates at any information rate up to a Theorem Theorem 10 − 10 critical rate C critical rate C, called , called channel capacity channel capacity. . 10 − 12 ε 10 − 14 Folk Theorem Folk Theorem 1 1 1 1 1 1 Choose as Choose as Channel Channel “All codes are good, except those we can think of. “ All codes are good, except those we can think of.” ” 11 3 5 7 9 small as small as Capacity Capacity you like you like Info Bits = Msg Rate C All Bits Hamming (8,4) 4 Code Hamming (8,4) 4 Code Types of Codes Types of Codes Info Words Info Words Code Words Code Words • Corrects all single errors • 0000 0000 0000 0000 0000 0000 • A • Corrects all single errors 0001 0001 1101 0001 1101 0001 • Detects all single, double, • A block code block code is a code that uses sequences is a code that uses sequences 0010 0010 0111 0010 0111 0010 Detects all single, double, of n channel symbols, or n n- -tuples tuples. . of n channel symbols, or 0011 0011 1010 0011 1010 0011 and triple errors and triple errors • Rate 0100 0100 1011 0100 1011 0100 • Rate R = 1/2 R = 1/2 0101 0101 0110 0101 0110 0101 Only certain selected Only certain selected n n- -tuples tuples, called , called 0110 0110 1100 0110 1100 0110 code blocks code blocks or or code words code words are sent. are sent. 0111 0001 0111 We will now apply this code We will now apply this code 0111 0001 0111 1000 1000 1110 1000 1110 1000 code to the BEC with code to the BEC with p=10 p=10 - -2 2 • Convolutional • 1001 1001 0011 1001 0011 1001 ∑ Convolutional Codes: Codes: − < < − − ≈ − 1010 1010 1001 1010 1001 1010 8 8 8 4 4 k k P C p (1 p ) C p (1 p ) Each output bit depends on all the previous U k 4 1011 1011 0100 1011 0100 1011 Each output bit depends on all the previous ( ( ) ) ( ) k 4 4 1100 0101 1100 ∴ ∴ < < − − − − − 1100 0101 1100 bits. bits. 2 2 70 10 1 10 P 1101 1101 1000 1101 1000 1101 U 1110 1110 0010 1110 0010 1110 ∴ ∴ < < × − 7 6.72 10 P 1111 1111 1111 1111 1111 1111 U 2
Terminology Decoding Table for a Block Code Terminology Decoding Table for a Block Code Codewords Codewords Code Code 11000 11000 00110 00110 10011 10011 01101 01101 11001 11001 00111 00111 10010 10010 01100 01100 00 11000 11010 11010 00100 00100 10001 10001 01111 01111 01 00110 11100 11100 00010 00010 10111 10111 01001 01001 10000 10000 01110 01110 11011 11011 00101 00101 10 10011 01000 10110 00011 11101 01000 10110 00011 11101 11 01101 Received Received 11110 00000 01011 10101 11110 00000 01011 10101 Words Words 01010 01010 10100 10100 11111 11111 00001 00001 Encoding Encoding Code Code Info Info Procedure Procedure Words Words Words Words Convolutional Convolutional Codes Codes Types of Error Correcting Codes Types of Error Correcting Codes Block Codes Block Codes Infinite Infinite Infinite Infinite • Orthogonal Codes • Input Output Input Output Orthogonal Codes • Linear Codes • Linear Codes • Cyclic Codes • � � � � Convolver Convolver a a aaa b b bbb Cyclic Codes + + n 1 n 2 1 0 n 1 n 2 1 0 • BCH Codes • BCH Codes Convolutional Convolutional Codes Codes • Threshold Decoding • Threshold Decoding • Sequential Decoding • Sequential Decoding Definitions Block Codes Definitions Block Codes Def. A Def. A code code is a set of binary vectors of is a set of binary vectors of the same fixed length the same fixed length Non- Non -Linear Linear Parameters of codes Parameters of codes Linear Linear n = n = length length of code vectors of code vectors R = R = code code rate rate = = (# info bits)/n (# info bits)/n Cyclic Cyclic P P U U = = Prob. Prob. of undetectable error of undetectable error BCH BCH 3
Recommend
More recommend