02/05/2014 4.1.2 Built-in Potential N-type P-type (a) N d N d N - PDF document

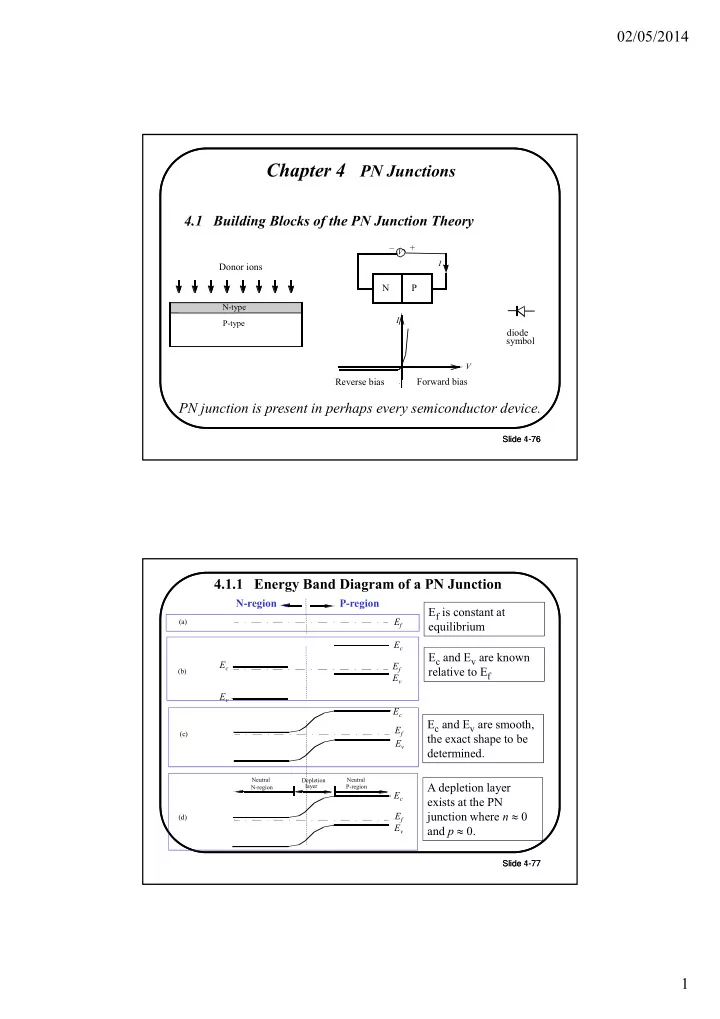
02/05/2014 Chapter 4 PN Junctions 4.1 Building Blocks of the PN Junction Theory – + V I Donor ions N P N-type I P-type diode symbol V Forward bias Reverse bias PN junction is present in perhaps every semiconductor device. Slide 4-76 Slide 1-76 4.1.1 Energy Band Diagram of a PN Junction N-region P-region E f is constant at E f (a) equilibrium E c E c and E v are known E c E f relative to E f (b) E v E v E c E c and E v are smooth, E f (c) the exact shape to be E v determined. Neutral Depletion Neutral A depletion layer layer N-region P-region E c exists at the PN junction where n  0 E f (d) E v and p  0. Slide 4-77 Slide 1-77 1

02/05/2014 4.1.2 Built-in Potential N-type P-type (a) N d N d N a N a E c q  bi (b) E f E v V  bi (c) x x N x P 0 Can the built-in potential be measured with a voltmeter? Slide 4-78 Slide 1-78 4.1.2 Built-in Potential kT N      q A kT N-region n N N e A ln c d c q N d 2 n kT N N    q B kT   P-region n i N e B ln c a c 2 N q n a i   kT N N N        B A ln c a ln c   bi 2 q n N   d i kT N N   ln d a bi 2 q n i Slide 1-79 Slide 4-79 2

02/05/2014 4.1.3 Poisson’s Equation Gauss’s Law: E ( x +  x ) E ( x )   s : permittivity (~12  o for Si)  : charge density (C/cm 3 )  x x Poisson’s equation Slide 4-80 Slide 1-80 4.2 Depletion-Layer Model 4.2.1 Field and Potential in the Depletion Layer On the P-side of the Neutral Region Depletion Layer Neutral Region depletion layer,  = – qN a N P x x 0 N P n p d E qN    a  dx s qN d qN qN x      P p E ( x ) a x C a ( x x ) x x  1  P n N – qN s s a On the N-side ,  = qN d  E qN   d - E ( x ) ( x x ) N x x x p s 0 n N P Slide 4-81 Slide 1-81 3

02/05/2014 4.2.1 Field and Potential in the Depletion Layer Neutral Region Depletion Layer Neutral Region N P – x n x 0 N p P The electric field is continuous at x = 0. N a |x P | = N d |x N | Which side of the junction is depleted more? A one-sided junction is called a N + P junction or P + N junction Slide 4-82 Slide 1-82 4.2.1 Field and Potential in the Depletion Layer On the P-side,  E qN   2 V ( x ) a ( x x ) P  2 s x x x p 0 n N P Arbitrarily choose the V  bi voltage at x = x P as V = 0. x x x On the N-side, P n N p E qN c    2 V ( x ) D d ( x x )   bi , built-in potential N  2 E s f E qN v     2 d ( x x ) bi N  2 s Slide 4-83 Slide 1-83 4

02/05/2014 4.2.2 Depletion-Layer Width Neutral Region Depletion Layer Neutral Region N P – x n x p 0 N P V is continuous at x = 0   2   1 1       x x W s bi   P N dep q N N   a d If N a >> N d , as in a P + N junction,   2 | | | |     W s bi x x x N N 0 dep N P N d a qN d What about a N + P junction? 1 1 1 1    where    W 2 qN N N N lighter dopant density dep s bi d a Slide 4-84 Slide 1-84 EXAMPLE : A P + N junction has N a =10 20 cm -3 and N d =10 17 cm -3 . What is a) its built in potential, b)W dep , c)x N , and d) x P ? Solution : a)  20  17 6 kT N N 10 10 cm     ln d a 0 . 026 V ln 1 V bi 2  q 10 20 cm 6 n i 1 / 2          2 2 12 8 . 85 10 14 1 b)      W s bi 0 . 12 μ m   dep   19  17 qN 1 . 6 10 10   d   c) x W 0 . 12 μ m N dep       4 d) x x N N 1 . 2 10 μ m 1 . 2 Å 0 P N d a Slide 4-85 Slide 1-85 5

02/05/2014 4.3 Reverse-Biased PN Junction V – + N P      2 ( | V |) 2 potential barrier E c   W s bi r s q  bi dep qN qN E c E f E f E v E v 1 1 1 1 (a) V = 0    N N N lighter dopant density E c d a q  bi + qV E fp • Does the depletion layer E v qV E c widen or shrink with E fn increasing reverse bias? E v (b) reverse-biased Slide 4-86 Slide 1-86 4.4 Capacitance-Voltage Characteristics N P N d N a Conductor Insulator Conductor W dep  Reverse biased PN junction is  C A s dep W a capacitor. dep • Is C dep a good thing? • How to minimize junction capacitance ? Slide 4-87 Slide 1-87 6

02/05/2014 4.4 Capacitance-Voltage Characteristics 1/ C dep 2 Capacitance data 2 W   1 2 ( V )  dep  bi 2 2  2 2  qN A C A S dep s Slope = 2/ qN  s A 2 V r –  b i Increasing reverse bias • From this C-V data can N a and N d be determined? Slide 4-88 Slide 1-88 EXAMPLE: If the slope of the line in the previous slide is 2x10 23 F -2 V -1 , the intercept is 0.84V, and A is 1  m 2 , find the lighter and heavier doping concentrations N l and N h . Solution:    2 N 2 /( slope q A ) l s      23   19    14  8 2 2 /( 2 10 1 . 6 10 12 8 . 85 10 10 cm )   15  3 6 10 cm  2 q 0 . 84 20 kT N N n 10 bi         18 3 ln h l N i e e 1 . 8 10 cm kT 0 . 026 bi h 2  15 q n N 6 10 i l • Is this an accurate way to determine N l ? N h ? Slide 4-89 Slide 1-89 7

02/05/2014 4.5 Junction Breakdown I Forward Current V B , breakdown voltage V R Small leakage Current A P N R C A 3.7 V IC Zener diode B D A Zener diode is designed to operate in the breakdown mode. Slide 4-90 Slide 1-90 4.5.1 Peak Electric Field Neutral Region increasing reverse bias N+ N a P x p 0 1 / 2   qN  (a) 2    E ( 0 )  ( | V |)  E E p  bi r   E p s increasing reverse bias  2 E    s crit V x B bi 2 qN x p (b) Slide 4-91 Slide 1-91 8

02/05/2014 4.5.2 Tunneling Breakdown Dominant if both sides of a junction are very heavily doped. Filled States - Empty States E c ε E v  H /  J G e p I   E E 6 10 V/cm V p crit Breakdown Slide 4-92 Slide 1-92 4.5.3 Avalanche Breakdown • impact ionization : an energetic E electron generating electron and c original hole, which can also cause electron E impact ionization. fp E • Impact ionization + positive v feedback  avalanche breakdown  2 E  crit s V electron-hole B 2 qN pair generation 1 1 1 E    V c E B N N N fn a d Slide 4-93 Slide 1-93 9

02/05/2014 4.6 Forward Bias – Carrier Injection Forward biased V = 0 V=0 Forward biased V I=0 – + E c N P  q  bi - E c E f q  bi – qV E v E fn qV E fp E v + Drift and diffusion cancel out Minority carrier injection Slide 4-94 Slide 1-94 4.6 Forward Bias – Quasi-equilibrium Boundary Condition      ( E E ) / kT ( E E ) / kT ( E E ) / kT   n ( x P ) N e N e e c fn c fp fn fp c c  ( E E ) / kT   qV / kT n e n e fn fp P 0 P 0 E c E c E fn • The minority carrier E fn E fn E fp densities are raised E fp by e qV/kT E v E v • Which side gets more carrier injection? x x x N x P 0 N 0 P Modern Semiconductor Devices for Integrated Circuits (C. Hu) Slide 4-95 Slide 1-95 10

02/05/2014 4.6 Carrier Injection Under Forward Bias– Quasi-equilibrium Boundary Condition 2 n   q V kT q V kT n x P ) n e i e ( P 0 N a 2 n   q V kT q V kT p ( x P ) p e i e N 0 N d     qV kT  n ( x ) n ( x ) n n ( e 1 ) P P P 0 P 0      qV kT p ( x ) p ( x ) p p ( e 1 ) N N N 0 N 0 Slide 1-96 Slide 4-96 EXAMPLE: Carrier Injection A PN junction has N a =10 19 cm -3 and N d =10 16 cm -3 . The applied voltage is 0.6 V. Question : What are the minority carrier concentrations at the depletion-region edges? Solution :  q V kT   0 . 6 0 . 026  11 -3 n ( x ) n e 10 e 10 cm P P 0  q V kT  4  0 . 6 0 . 026  14 -3 p ( x ) p e 10 e 10 cm N N 0 Question : What are the excess minority carrier concentrations?     11   11 -3 Solution : n ( x ) n ( x ) n 10 10 10 cm P P P 0     14  4  14 -3 p ( x ) p ( x ) p 10 10 10 cm N N N 0 Slide 4-97 Slide 1-97 11

02/05/2014 4.7 Current Continuity Equation   J ( x ) J ( x x )  p  p   p     A A A x  q q A a e r a J p ( x ) J p ( x +  x )     J ( x x ) J ( x ) p  p p  q p   x  dJ p p Volume = A ·  x   q  dx  x  x Slide 4-98 Slide 1-98 4.7 Current Continuity Equation dJ p  p Minority drift current is negligible;   q  dx  J p = – qD p dp/dx  2 d p p  qD q p  2 dx p   2 d n n    2 d p p p    2 2 dx 2  2 L dx D L n p p p L p and L n are the diffusion lengths     L D L D n n n p p p Slide 4-99 Slide 1-99 12