UMBC A B M A L T F O U M B C I M Y O R T 1 - PowerPoint PPT Presentation

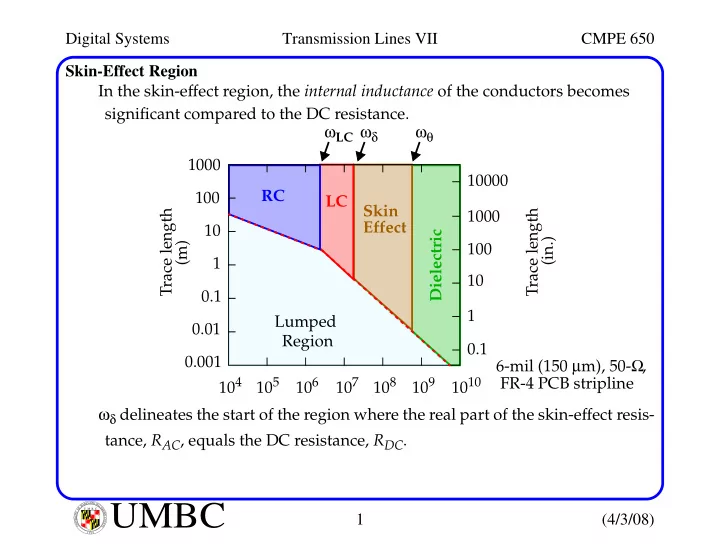
Digital Systems Transmission Lines VII CMPE 650 Skin-Effect Region In the skin-effect region, the internal inductance of the conductors becomes significant compared to the DC resistance. ω LC ω δ ω θ 1000 10000 RC 100 LC Skin Trace length Trace length 1000 Effect 10 Dielectric (in.) (m) 100 1 10 0.1 1 Lumped 0.01 Region 0.1 0.001 6-mil (150 µ m), 50- Ω , 10 4 10 5 10 6 10 7 10 8 10 9 10 10 FR-4 PCB stripline ω δ delineates the start of the region where the real part of the skin-effect resis- tance, R AC , equals the DC resistance, R DC . L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 1 (4/3/08) I E S R C E O V U I N N U T Y 1 6 9 6

Digital Systems Transmission Lines VII CMPE 650 Skin-Effect Region Recalling from previous discussions k p k r ωµ k a ρ [ ] Re R AC = - - - - - - - - - - - - - - - - - - - - - - - - R DC = - - - - - - - - - p 2 σ a ω δ is given by  2  R DC ω δ ω 0   = - - - - - - - - - - - R 0   Here, ω 0 is a frequency well into the skin-effect region and R 0 is the value of R AC at that frequency. In skin-effect mode, the characteristic impedance remains fairly flat but the line attenuation in dB varies in proportion to the square root of frequency . Characteristic impedance is given by j ω L 0 R ω ( ) + = - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Z C j ω C L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 2 (4/3/08) I E S R C E O V U I N N U T Y 1 6 9 6

Digital Systems Transmission Lines VII CMPE 650 Skin-Effect Characteristic Impedance The term L 0 refers to the external inductance of the line, since internal induc- tance is accounted for in R( ω ) . External inductance is the value of series inductance assuming that current rides on the surface without penetrating the wire. As you proceed to higher frequencies above ω δ , the contribution of R( ω ) becomes negligable, leaving j ω L 0 R ω ( ) ∆ + L 0 = lim - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - = - - - - - - Z 0 j ω C C ω → ∞ This indicates that although R( ω ) grows in proportion to the square root of frequency, j ω L 0 grows more quickly. Therefore, once past the cross-over ω LC (remember, this is where the induc- tance impedance equals the DC resistance), R( ω ) diminishes in importance. L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 3 (4/3/08) I E S R C E O V U I N N U T Y 1 6 9 6

Digital Systems Transmission Lines VII CMPE 650 Skin-Effect Propagation Coefficient Because the skin-effect onset is so close to the LC-mode onset, the flat region for the real part is very small. Natural logarithmic units 10 (radians or nepers) Im( γ ) 1 skin-effect PCB trace Re( γ ) loss proportional to f 1/2 0.1 DC resistance only Re( γ ) is flat 0.01 10 5 10 6 10 7 10 8 10 9 10 10 Freq. (Hz) ω LC ω δ As indicated, after ω δ , attenuation (in dB) increases proportional to the square root of frequency. The decoupling of phase and attenuation enable the construction of a line with an enormous phase delay and yet very low attenuation. L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 4 (4/3/08) I E S R C E O V U I N N U T Y 1 6 9 6

Digital Systems Transmission Lines VII CMPE 650 Skin-Effect Propagation Coefficient Propagation function assuming operation at a frequency well in excess of ω δ so that R AC >> R DC γ ω ( ) ( j ω L 0 ) j ω C ( ) = + R AC Factoring out common j ω L 0 and j ω C terms R AC γ ω ( ) ( j ω L 0 ) j ω C ( ) 1 = + - - - - - - - - - - - j ω L Assuming ω >> ω LC so that |j ω L 0 | >> |R AC |   R AC 1 γ ω ( ) ( j ω L 0 ) j ω C ( ) 1   = + - - - - - - - - - - - - - - - - j ω L 0 2   Distributing R AC 1 γ ω ( ) ( j ω L 0 ) j ω C ( ) ( j ω L 0 ) j ω C ( ) - - - - - - - - - - - - - - - = + j ω L 0 2 L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 5 (4/3/08) I E S R C E O V U I N N U T Y 1 6 9 6

Digital Systems Transmission Lines VII CMPE 650 Skin-Effect Propagation Coefficient Combining and substituting for characteristic impedance R AC 1 γ ω ( ) ( j ω L 0 ) j ω C ( ) - - - - - - - - - - - - - - = + 2 Z 0 Factoring out j ω on the left and substituting expression for R AC described earlier R 0 ( ) ω 1 + j γ ω ( ) j ω L 0 C = + - - - - - - - - - - - - - - - - - - - - - - - - - - - - - ω 0 2 Z 0 Like the LC region, the first term indicates linear phase and represent the bulk transport delay. ∆ 1 = - - - - - = L 0 C s/m t p v 0 The second term is a low-pass filter whose attenuation in dB grows propor- tional to the sqrt(f) . L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 6 (4/3/08) I E S R C E O V U I N N U T Y 1 6 9 6

Digital Systems Transmission Lines VII CMPE 650 Skin-Effect Propagation Coefficient Similar to the LC region, the skin-effect loss coefficient can be defined R 0 R 0 ∆ ω ω 1 α r Re γ ω [ ( ) ] - - - - - - - - - - - - - - - = = - - - - - - - neper/m = 4.34 - - - - - - dB/m - ω 0 ω 0 2 Z 0 Z 0 The low-pass filtering action will slur the rising edge of the step response, adding slew. R 0 ω l 1 – - - - - - - - - - - - - - - - ω 0 2 Z 0 H ω l ( , ) = e Here again, doubling length, doubles the signal loss. However, here signal loss is also frequency dependent , doubling the fre- quency multiplies the loss by the sqrt(2) . The termination approaches discussed with reference to the LC region work here as well (and in the dielectric-loss-limited region). This is true because all three regions share the same asymptotic high-fre- quency value of characteristic impedance Z 0 . L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 7 (4/3/08) I E S R C E O V U I N N U T Y 1 6 9 6

Digital Systems Transmission Lines VII CMPE 650 Dielectric-Loss-Limited Region Dielectric-loss increases the slope of the Re( γ ) Natural logarithmic units 10 (radians or nepers) ∝ Im( γ ) Dielectric loss f 1 ∝ PCB trace Skin-effect loss f 0.1 DC resistance only Re( γ ) is flat 0.01 10 5 10 6 10 7 10 8 10 9 10 10 Freq. (Hz) ω LC ω δ ω θ It is common in PCB problems to see skin-effect losses AND dielectric losses. Waveguide-dispersion region begins when the frequency of the signal approaches the dimensions of your conductor. For a stripline, the critical dimension is the spacing between the planes. Strange modes appear, severe ringing occurs under perfect termination. L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 8 (4/3/08) I E S R C E O V U I N N U T Y 1 6 9 6

Digital Systems Transmission Lines VII CMPE 650 Example Specs • Length l = 0.6 m (23.6 in.) (backplane application) • Conductor parameters: w = 152 µ m (6 mil), t = 17.4 µ m (1/2 oz. Cu), perim- eter p = 2(w + t ) = 339 µ m (13.35 mil) • Conductivity of signal conductor σ = 5.98 x 10 7 S/m • Specification frequency for AC parameters: ω 0 = 2 π x 10 9 • Characteristic impedance at ω 0 : Z 0 = 100 Ω • Effective dielectric constant ε R = 4.3 • Effective loss tangent for FR-4 dielectric: tan θ 0 = 0.025 • Proximity factor k p = 3.2 Computed values • Propagation velocity above RC region c 8 × 10 m/s v 0 = - - - - - - - - - - = 1.4457 t p = 175.7 ps/in. ε R L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 9 (4/3/08) I E S R C E O V U I N N U T Y 1 6 9 6

Digital Systems Transmission Lines VII CMPE 650 Example • Differential inductance per meter Z 0 L = - - - - - - = 691 nH/m v 0 • Differential capacitance per meter 1 C = - - - - - - - - - - - - = 69.1 pF/m Z 0 v 0 • DC resistance 2 12.64 Ω /m R DC = - - - - - - - - - - - - - - - = ( σ w t ) • AC resistance ω 0 µ k p 76.74 Ω /m R 0 = - - - - - - - - - - - - - - - - = 2 σ p L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 10 (4/3/08) I E S R C E O V U I N N U T Y 1 6 9 6

Digital Systems Transmission Lines VII CMPE 650 Example Lumped-element region  0.25  L critical length = - - - - - - - - - - - - - - - = 1.97 m   R DC C The trace length of l = 0.6 m falls short of the critical length, so we move from lumped-element directly to LC, skipping the RC region. Other region transitions Note: ω values multiplied by 1/(2 π ) ∆   ω LC LC Region = - - - LC = 9.58 MHz   l  2  R DC ω δ ω 0   Skin-effect - - - - - - - - - - - = = 27.1 MHz R 0   ( ) 2 v 0 R 0 1 ω θ Dielectric (haven’t covered) - - - - - - - - - - - - - - - - - - - - - - - - - - - - = = 498 MHz ω 0 θ 0 Z 0 tan L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 11 (4/3/08) I E S R C E O V U I N N U T Y 1 6 9 6