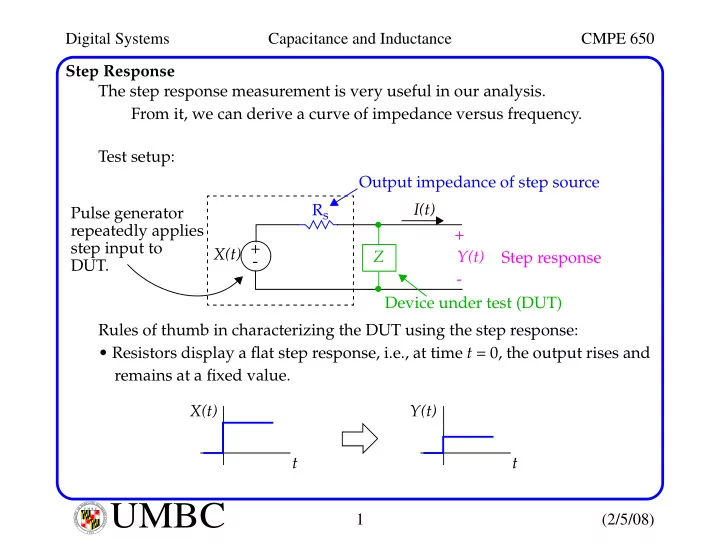

Digital Systems Capacitance and Inductance CMPE 650 Step Response The step response measurement is very useful in our analysis. From it, we can derive a curve of impedance versus frequency. Test setup: Output impedance of step source I(t) R s Pulse generator repeatedly applies + step input to X(t) + Z Y(t) Step response - DUT. - Device under test (DUT) Rules of thumb in characterizing the DUT using the step response: • Resistors display a flat step response, i.e., at time t = 0, the output rises and remains at a fixed value. X(t) Y(t) t t L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 1 (2/5/08) I E S R C E O V U I N N U T Y 1 6 9 6
Digital Systems Capacitance and Inductance CMPE 650 Step Response • Capacitors display a rising step response, i.e., at time t = 0, the output starts rising and later reaches its full value. X(t) Y(t) t t • Inductors display a sinking step response, i.e., at time t = 0, the output rises instantly to its full value and then later decays back toward 0. X(t) Y(t) t t Capacitors and inductors subdivide into ordinary and mutual categories. Ordinary capacitance and inductance (two-terminal devices) can be a help or hindrance. Mutual capacitance and inductance usually creates unwanted crosstalk. L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 2 (2/5/08) I E S R C E O V U I N N U T Y 1 6 9 6
Digital Systems Capacitance and Inductance CMPE 650 Capacitance The capacitor is a 2-terminal element in which the branch voltage and current variables are related by integral and differential equations: t (Voltage on Cdv 1 ∫ ( ) ( ) i τ ( ) τ ( ) i t v t d v t 0 and = - - - - + = - - - - - - cap depends C dt on history of i ) t 0 Charge and voltage are related by the linear relationship: q slope = C ( ) ( ) q t Cv t = v Power is negative or positive depending on the value of the term v(t)dv/dt in the following expression ( ) dv ( ) p t Cv t - - - - - - = dt L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 3 (2/5/08) I E S R C E O V U I N N U T Y 1 6 9 6
Digital Systems Capacitance and Inductance CMPE 650 Capacitance But energy (the integral of power) is always positive or zero: Cv 2 t ( ) ( ) w t = - - - - - - - - - - - - - - - - - 2 Therefore, it’s a passive element (like the resistor) but it is non-dissipa- tive (unlike the resistor). All the energy supplied to the cap. is stored in the electric field. Note that the voltage appearing across a capacitor must always be a continu- ous function (voltage steps not allowed -- require an infinite i ). Current, on the other hand, is allowed to change instantenously. v(t) i(t) + t t i(t) v(t) v(t) i(t) - t t L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 4 (2/5/08) I E S R C E O V U I N N U T Y 1 6 9 6
Digital Systems Capacitance and Inductance CMPE 650 Capacitance The energy stored in the electric field of a capacitor is supplied by the driving circuit. Since the driving source is a limited source of power, the voltage takes a finite time to build up. The reluctance of voltage to build up quickly in response to injected power (or decay quickly) is called capacitance . X(t) R s = 30 Ω I(t) max value V CC /R + I(t) + X(t) Y(t) - - Y(t) voltage approaches V CC Y(t) impedance I(t) short circuit open circuit 1 ns L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 5 (2/5/08) I E S R C E O V U I N N U T Y 1 6 9 6
Digital Systems Capacitance and Inductance CMPE 650 Capacitance Bear in mind that a capacitor behaves like an inductor at high frequencies (unfortunately). This is due to the mounting leads on capacitors. This inductance causes the step response to have a tiny pulse (a couple hundred ps) at time 0, followed by a drop to 0 and then a capacitive ramp. Note that you will not be able to see this unless your step source rise time is sharp. At T r , you can characterize the circuit element for frequencies up to: 0.5 F A = - - - - - - - T r Reactance on leading edge (to est. distortion in digital wfm by a cap.): T r X C = - - - - - - - π C L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 6 (2/5/08) I E S R C E O V U I N N U T Y 1 6 9 6
Digital Systems Capacitance and Inductance CMPE 650 Capacitance Test Gig A measurement setup ideal for characterizing capacitors: 50 Ω Pulse Scope generator termination 50 Ω + 1 square inch - + V(t) - 1 K Ω 1 K Ω 50 Ω back termination 50 Ω reduces output by 1/2 DUT can be a circuit DUT trace, a bypass cap, etc. Note that the resistances are known, so by measuring the rise time of the resulting waveform, the capacitance of the DUT can be computed. The test gig is dimensioned at 1 square inch to ensure it behaves in a lumped fashion. The test gig should include a ground plane of 1 square inch. L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 7 (2/5/08) I E S R C E O V U I N N U T Y 1 6 9 6
Digital Systems Capacitance and Inductance CMPE 650 Inductance The inductor is a 2-terminal element in which the branch voltage and current variables are related by integral and differential equations: t Ldi 1 ∫ ( ) ( ) v τ ( ) τ ( ) v t i t d i t 0 and = - - - + = - - - - - L dt t 0 Flux linkages (in weber-turns) and current are related by the relationship: λ i n turns of wire slope = L + d λ ( ) λ t ( ) n φ t ( ) ( ) v t Li t = = = - - - - - - L v dt i - produces flux Power is negative or positive depending on the value of the term i(t)di/dt in the following expression ( ) Ldi ( ) ( ) v t ( ) p t i t i t - - - - - = = dt L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 8 (2/5/08) I E S R C E O V U I N N U T Y 1 6 9 6
Digital Systems Capacitance and Inductance CMPE 650 Inductance But energy (the integral of power) is always positive or zero: Li 2 t ( ) ( ) w t = - - - - - - - - - - - - - - - 2 Therefore, it’s a passive element (like the resistor) but it is non-dissipa- tive (unlike the resistor). All the energy supplied to the ind. is stored in the magnetic field. Note that the current flowing through an inductor must always be a continu- ous function (current steps not allowed -- require an infinite v ). Voltage, on the other hand, is allowed to change instantenously. i(t) v(t) t t + v(t) i(t) - i(t) v(t) t t L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 9 (2/5/08) I E S R C E O V U I N N U T Y 1 6 9 6
Digital Systems Capacitance and Inductance CMPE 650 Inductance The energy stored in the magnetic field of a inductor is supplied by the driv- ing circuit. Since the driving source is a limited source of power, the current takes a finite time to build up. The reluctance of current to build up quickly in response to injected power (or decay quickly) is called inductance . X(t) current approaches V CC /R R s = 30 Ω I(t) + I(t) + voltage output decays to 0. X(t) Y(t) - - Y(t) Y(t) impedance I(t) open circuit short circuit 1 ns L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 10 (2/5/08) I E S R C E O V U I N N U T Y 1 6 9 6
Digital Systems Capacitance and Inductance CMPE 650 Inductance Test Gig A measurement setup ideal for characterizing inductors: 50 Ω Pulse Scope generator termination 50 Ω + 1 square inch - + V(t) - 39 Ω 50 Ω back termination 10 Ω reduces output by 1/2 DUT Reactance on leading edge (to est. distortion in digital wfm by an inductive load: π L X L = - - - - - - - T r L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 11 (2/5/08) I E S R C E O V U I N N U T Y 1 6 9 6
Digital Systems Capacitance and Inductance CMPE 650 Measuring Inductance Inductance can be measured in a similar way to capacitance by computing the time, for example, in the response waveform to the 63% point. A second method for inductance involves computing the area under the response waveform’s curve: ∞ ∞ ( ) d I ind t Ldi ∫ ( ) t ∫ V ind t d L - t d ( ) v t = - - - - - - - - - - - - - - - - - - = - - - - - dt dt 0 0 ∞ ∫ ( ) t L I ∞ [ ( ) ( ) ] V ind t d I 0 = – Inductor acts as a short 0 circuit at time (infinity) therefore delta V/R S L I ∞ [ ( ) ( ) ] area I 0 = – gives the current. ( ) R S area area where R S and ∆ V L = - - - - - - - - - - - - = - - - - - - - - - - - - - - - - - - - - - - - ∆ I ∆ V are the open circuit ∆ V ∆ I response values = - - - - - - - - R S (see Example 1.2) L A N R Y D UMBC A B M A L T F O U M B C I M Y O R T 12 (2/5/08) I E S R C E O V U I N N U T Y 1 6 9 6
Recommend
More recommend