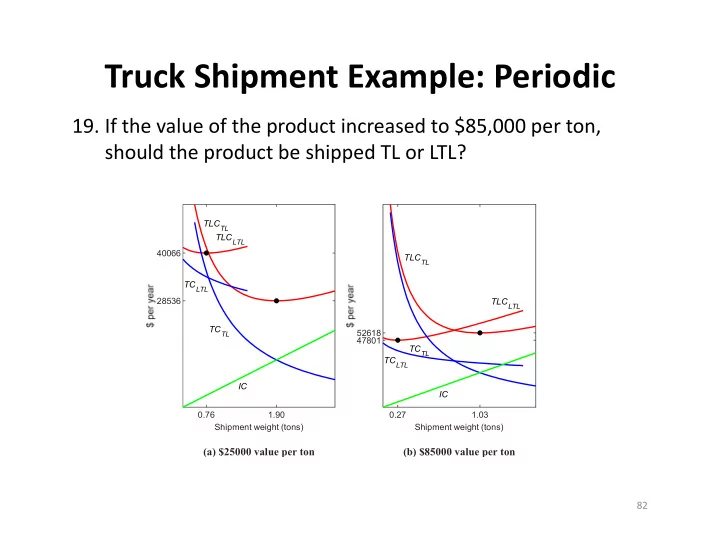

Truck Shipment Example: Periodic 19. If the value of the product increased to $85,000 per ton, should the product be shipped TL or LTL? TLC TL TLC LTL 40066 TLC TL TC LTL 28536 TLC LTL TC TL 52618 47801 TC TL TC LTL IC IC 0.76 1.90 0.27 1.03 Shipment weight (tons) Shipment weight (tons) (a) $25000 value per ton (b) $85000 value per ton 82
Truck Shipment Example: Periodic • Better to pick from separate optimal TL and LTL because independent charge has two local minima: ! f * * { } = arg min ( ) + α = arg min ( ), ( ) q c q vhq q TLC q TLC q 0 0 0 TL LTL q q q 83
Truck Shipment Example: Periodic 20. What is optimal independent shipment size to ship 80 tons per year of a Class 60 product valued at $5000 per ton, with the same inventory fraction and carrying rate, between Raleigh and Gainesville? 3 = s 32.16 lb/ft * { } = arg min ( ), ( ) = 8.5079 ton q TLC q TLC q 0 TL LTL q * * ( ) = $25,523.60 / yr < ( ) TLC q TLC q 0 0 TL LTL 84
Truck Shipment Example: Periodic 21. What is the optimal shipment size if both shipments will always be shipped together on the same truck (with same shipment interval)? = , = = , α = α = α d d h h h 1 2 agg 1 2 agg 1 2 = + = 20 + 80 = 100 ton f f f agg 1 2 ( ) aggregate weight, in lb f 100 agg 3 = = = = 14.31lb/ft s agg ( ) 20 80 f f 3 aggregate cube, in ft 1 2 + + 4.44 32.16 s s 1 2 20 80 f f 1 2 = + = + = v v v 85,000 5000 $21,000 / ton agg 1 2 100 100 f f agg agg f r d 100(2.5511)532 agg TL * = = = 4.6414 ton q TL α (1)21000(0.3) v h agg agg agg 85
Truck Shipment Example: Periodic • Summary of results: 86
Ex 6: FTL vs Interval Constraint On average, 200 tons of components are shipped 750 miles from your fabrication • plant to your assembly plant each year. The components are produced and consumed at a constant rate throughout the year. Currently, full truckloads of the material are shipped. What would be the impact on total annual logistics costs if TL shipments were made every two weeks? The revenue per loaded truck-mile is $2.00; a truck’s cubic and weight capacities are 3,000 ft 3 and 24 tons, respectively; each ton of the material is valued at $5,000 and has a density of 10 lb per ft 3 ; the material loses 30% of its value after 18 months; and in-transit inventory costs can be ignored. 1 1 = 200, = 750, α = + = 1, = 2, = 3000, = 24, = 5000, = 10 f d r K K v s TL cu wt 2 2 0.3 x sK h cu = = = 0.2 = 0.05 + 0.06 + 0.2 = 0.31, = = min , = 15 h h q q K obs max FTL wt 1.5 2000 t h f = = 13.33, = + α = 43,250, 2-wk TL LTL not considered n TLC n r d vhq FTL FTL FTL TL FTL q FTL 2 7 ⋅ f = = = = = + α = t n 26.09, q 7.67, TLC n r d vhq 51,016 max min 2wk 2wk min TL 2wk 365.25 n min ∆ = − = TLC TLC TLC $7,766 per year increase with two-week interval constraint 2wk FTL 87
Ex 7: FTL Location • Where should a DC be located in order to minimize transportation costs, given: 36.5 Winston-Salem Greensboro Durham 1. FTLs containing mix of products 190 36 220 270 Raleigh Statesville 295 Asheville 150 A and B shipped P2P from DC to 35.5 50 customers in Winston-Salem, 40 35 W i Durham, and Wilmington l m i n g 34.5 t o n 420 2. Each customer receives 20, 30, 34 and 50% of total demand -83 -82 -81 -80 -79 -78 3. 100 tons/yr of A shipped FTL P2P to DC from supplier in Asheville 4. 380 tons/yr of B shipped FTL P2P to DC from Statesville Each carton of A weighs 30 lb, and occupies 10 ft 3 5. Each carton of B weighs 120 lb, and occupies 4 ft 3 6. 7. Revenue per loaded truck-mile is $2 Each truck’s cubic and weight capacity is 2,750 ft 3 and 25 tons, 8. respectively 88
Ex 7: FTL Location TC = w × d i i Winston- ($/yr) ($/mi-yr) (mi) Salem Asheville = × = × w f r n r , i i FTL i i i DC ($/mi-yr) (TL/yr) ($/TL-mi) (ton/yr) ($/ton-mi) Durham 30% r f r = , n = Statesville , FTL i Wilmington q q ($/ton-mi) max max f 480 10.4348(2750 agg 3 = $2 / TL-mi, = + = 100 + 380 = 480 ton/yr, = = = 10.4348 lb/ft , = 25, = 14.3478 r f f f s q agg A B agg max f f 100 380 2000 A B + + s s 3 30 30 3(2750) A B 3 = = = = s 3 lb/ft , q min 25, 4.125 ton 96 1 max = 0.20 = 96, = = 6.69, = 6.69(2) = 13.38 10 2000 f f n w 3 agg 3 3 14.3478 3 100 1 144 = = = = = f 100, n 24.24, w 24.24(2) 48.48 1 1 1 = 0.30 = 144, = = 10.04, = 10.04(2) = 20.07 f f n w 4.125 DC 4 4 agg 4 4 14.3478 120 30(2750) 2 3 240 s = = 30 lb/ft , q = min 25, = 25 ton 5 2 max = 0.50 = 240, = = 16.73, = 16.73(2) = 33.45 f f n w 4 2000 5 agg 5 5 14.3478 380 f = 380, n = = 15.2, w = 15.2(2) = 30.4 2 2 2 25 Asheville Statesville Winston-Salem Durham Wilmington : W w 30 13 20 33 48 i W = 146, = 73 2 48 < 73 78 > 73 * ( ) (Montetary) Weight Losing: Σ = 79 > Σ = 67 Σ = 39 > Σ = 33 w w n n in out in out Physically Weight Unchanging (DC): Σ = 480 = Σ = 480 f f in out 89
Ex 7: FTL Location • Include monthly outbound frequency constraint: – Outbound shipments must occur at least once each month – Implicit means of including inventory costs in location decision 1 1 = yr/TL = = 12 TL/yr t n max min 12 t max { } ′ = max , TC n n rd FTL min { } = max 6.69,12 = 12, = 12(2) = 24 n w 3 3 { } = max 10.04,12 = 12, = 12(2) = 24 n w 4 4 { } = max 16.73,12 = 16.73, = 16.73(2) = 33.45 n w 5 5 Asheville Statesville Winston-Salem Durham Wilmington W : w 48 30 24 24 33 W = 160, = 80 i 2 48 < 80 78 < 80 102 > 80 * ( ) (Montetary) Weight Ga ining : Σ = 79 < Σ = 81 Σ = 39 < Σ = 41 w w n n in out in out Physically Weight Unchanging (DC) : Σ = 480 = Σ = 48 0 f f in out 90
Location and Transport Costs • Monetary weights w used for location are, in general, a function of the location of a NF – Distance d appears in optimal TL size formula – TC & IC functions of location Need to minimize TLC instead of TC – FTL (since size is fixed at max payload) results in only constant weights for location Need to only minimize TC since IC is constant in TLC m m f i ( ) = ( ) ( ) + α ( ) = ( ) + α ( ) TLC x w x d x vhq x rd x vhq x TL i i i i i q ( ) x i = 1 = 1 i i m m ( ) 1 f f rd x i i i = ( ) + α = ( ) + α rd x vh f rd x vh i i i α vh ( ) α f rd x vh = 1 = 1 i i i i α vh m m f i ( ) = ( ) + α = ( ) + α = ( ) + con stant TLC x rd x vhq w d x vhq TC x FTL i max i i max FTL q max = = i 1 i 1 91
Transshipment • Direct : P2P shipments from Suppliers to Customers • Transshipment : use DC to consolidate outbound shipments – Uncoordinated : determine separately each optimal inbound and outbound shipment hold inventory at DC – (Perfect) Cross-dock : use single shipment interval for all inbound and outbound shipments no inventory at DC (usually only cross-dock a selected subset of shipments) 92
Uncoordinated Inventory • Average pipeline inventory level at DC: α = α + α O D 1 , α + inbound = O 2 + 0 α , outbound D Supplier 1 ≈ q 1.55 2 Supplier 2 ≈ q 1.11 2 93
TLC with Transshipment • Uncoordinated: = of supplier/customer TLC TLC i i * = arg min ( ) q TLC q i i q = ( ) * * TLC TLC q i i q = , shipment interval t • Cross-docking: f ( ) c t f 0 ( ) = + α cf. ( ) = ( ) + α TLC t vhft TLC q c q vhq 0 i i t q ( ) = independent transport charge as function of c t t 0 α + 0, inbound = + O α α 0 , outbound D * = arg min ( ) t TLC t i t ( ) * * = TLC TLC t i 94
Recommend
More recommend