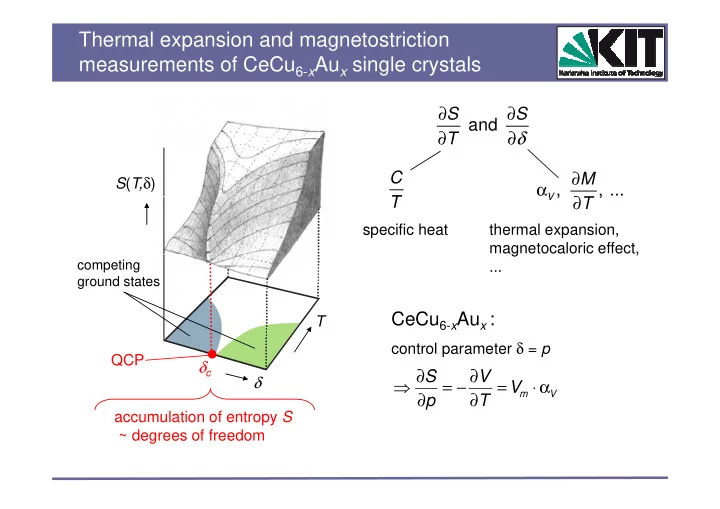
Thermal expansion and magnetostriction measurements of CeCu 6- x Au x - PowerPoint PPT Presentation

Thermal expansion and magnetostriction measurements of CeCu 6- x Au x single crystals ∂ ∂ S S and ∂ ∂ ∂ δ ∂ δ T T C ∂ M S ( T, δ ) , , , ... , α V V T T ∂ ∂ T T specific heat thermal expansion, magnetocaloric effect, g , competing ... ground states CeCu 6- x Au x : C C A T control parameter δ = p QCP δ δ c ∂ ∂ ∂ ∂ S S V V ⇒ δ = − = ⋅ α V m V ∂ p ∂ T accumulation of entropy S ~ degrees of freedom

Thermal expansion and magnetostriction measurements of CeCu 6- x Au x single crystals Different scenarios: traditional “itinerant” scenario “local” scenario ... T T T Kondo lattice T N T N T Kondo lattice FL FL ? J ~ V ( p , x ) J ~ V ( p , x ) ∂ S = α V ∂ p and scaling behavior and scaling behavior Coleman, Si et al.. Hertz, Millis, Moiya et al.

Outline Stefanie Drobnik 1 , Frédéric Hardy 1 , Kai Grube 1 , Roland Schäfer 1 , Peter Schweiss 1 , Oliver Stockert 2 , Thomas Wolf, Christoph Meingast 1 , and Hilbert v. Löhneysen 1 1 IFP Forschungszentrum Karlsruhe, PI Universität Karlsruhe, KIT, Germany 2 MPI für chemische Physik fester Stoffe, Dresden, Germany Introduction: Thermal expansion at a QCP Experimental details: dilatometer CeCu 6- x Au x : control parameter x and p Measurements: Thermal expansion: volume, lattice parameter (compressibility, magnetostriction) Summary and outlook Summary and outlook

Thermal expansion at a quantum critical point Fermi liquid for T → 0: α V / T → ∂γ / ∂ p = constant T classical fluctuations ordered NFL NFL phase dS = 0 ∂ S 0 0 p < < FL FL ∂ QCP α crit / T p |α NFL / T| ∂ ∂ S S 0 > ∂ p FL NFL L. Zhu et al. PRL 91, 066404 (2003) M. Garst et al. PRB 72, 205129 (2005) T P. Gegenwart et al. PRL 96, 136402 (2006) M. Garst et al. : cond-mat 0808.0616

Experimental details Capacitance dilatometer: Capacitance dilatometer: thermal expansion & magnetostriction a) 40 mK < T < 10 K, µ 0 H < 14 T m 20 mm b) 1 5 K < T < 300 K µ H < 10 T b) 1.5 K < T < 300 K, µ 0 H < 10 T rotatable in H ∆ L > 0.01 Å, ∆ L / L 10 -9 plate capacitor sample mm 5 m c) Miniature dilatometer built in a He gas pressure cell: a He-gas pressure cell: compressibility measurements 10 K < T < 325 K, p < 8 kbar ∆ L > 0.1 Å, ∆ L / L 10 -8 Å

CeCu 6- x Au x : control parameter x and p For x < 1.0: 1.6 T N x = 0 5 0.5 T N 2.0 2 0 x N N (K) (K) 1.4 1.5 1.2 1.0 1.0 0.5 0.8 AF AF AF AF 0.6 0.0 0.0 0.5 1.0 0.0 0.5 1.0 p (GPa) p ( ) x V V Comparison between the control parameters x and p

CeCu 6- x Au x : control parameter gold content x x Cu(2) → Au ( ) 0 0 0.0 0 5 0.5 1 0 1.0 1.5 1 5 445 440 Ce V 435 (Å) Å 430 Cu 425 Cu(2) Cu(4) 420 b c a 8.3 5.12 a,b,c ( x ) 10.4 c (Å) ( ) 8.2 5.10 5 10 10.2 a orthorhombic 8.1 5.08 b Pnma structure 0 1 0 1 0 1 (Å) (Å) (Å) x x x residual resistivity y For x < 1 0 For x < 1.0 • strongly anisotropic distortion of the lattice • introduction of disorder x

CeCu 6- x Au x : hydrostatic pressure p x Au 1.000 1.000 T = 300 K x = 0 a / a 0 Ce b / b b / b 0 Cu c / c 0 1.000 0.999 V / V 0 0.998 c 0.0 0.1 0.2 0.3 a orthorhombic 0.0 0.1 0.2 0.3 b Pnma structure p (GPa) If V ( x ) = V ( p ): usually a ( x ) ≠ a ( p ), b ( x ) ≠ b ( p ), c ( x ) ≠ c ( p ) and ρ 0 ( V ( x )) ≠ ρ 0 ( V ( p )).

Comparison of x and p At the QCP, CeCu 6- x M x (M = Au, Pd, Pt) C p / T show the identical NFL behavior (J/molK 2 ) but differ: • • in their lattice parameters in their lattice parameters • and the amount of disorder T N AF x x T (K) ⇒ for x ≤ 0.3: doping with Au = chemical pressure ~ applying negative hydrostatic pressure ⇓ control parameter: volume V control parameter: volume V

Thermal expansion of CeCu 6- x Au x Ce(4f 1 )Cu 5.85 Au 0.15 50 α V (10 -6 K -1 ) Grüneisen ratio: 40 1 * 1 ∂ θ α ∂ E 30 30 Debye Debye Γ Γ = V V ≈ → p * ∂ θ ∂ C E p p La(4f 0 )Cu 6 p Debye 20 C p 10 150 (J/molK) 0 0 100 100 0 50 100 150 200 250 300 T (K) 50 typical for HF systems: 0 0 50 100 150 200 250 300 T (K) large 4(5)f contribution to the thermal expansion g ( ) p

Thermal expansion: 4f contribution 4f 1 contribution to α V = α V (Ce(4f 1 )Cu 5 85 Au 0 15 ) - α V (La(4f 0 )Cu 6 ) 4f contribution to α V α V (Ce(4f )Cu 5.85 Au 0.15 ) α V (La(4f )Cu 6 ) 15 α V (4f) (10 -6 K -1 ) (10 6 K 1 ) 10 T N 4f 1 contribution to C p 5 5 T N T N C p (4f) 4 (J/molK) AF 0 0 3 0.1 1 10 100 x 2 T (K) T N 1 AF order Kondo lattice CEF 0 0.1 1 10 100 ∆ CEF (meV) T (K) 0 – 7 – 13.8

Linear thermal expansion coefficients α i α V = α a + α b + α c α = α + α + α α i ~ - ∂ S / ∂σ i i = a , b , c 12 α a , b , c 10 10 (10 -6 K -1 ) uniaxial pressure 8 c in i direction 6 6 4 b 1 2 b,c α a,b 0 0 -2 a 0.05 T (K) T (K) 0.1 1 10 100 T (K) Anisotropy of changes α i d depending which characteristic di hi h h t i ti AF order Kondo lattice CEF energy scale dominates. ∆ CEF (meV) 0 – 7 – 13.8

Non-Fermi liquid behavior Fermi liquid for T → 0: q C / T → γ = constant α V / T → ∂γ / ∂ p = constant C p / T C / T 60 60 α V / T x = 0.15 4 x = 0.1 (J/ mol K 2 ) (10 -6 K -2 ) x = 0.5 x = 0.3 x = 0.15 40 3 3 x = 0.1 0 1 20 2 x = 0.0 x = 0.0 x = 0.3 T N 0 1 x = 0.5 0.5 x AF AF 0 -20 0.1 1 0.1 1 4 x T (K) T (K) T (K) T (K) Non-Fermi liquid behavior next to the onset of AF order. thermal expansion measurements for x = 0, 0.3, 0.5 from A. de Visser et al.

Grüneisen parameter Γ V of CeCu 6- x Au x If the system is dominated by a characteristic energy scale E * If the system is dominated by a characteristic energy scale E * Γ V reveals the (normalized) volume dependence of E *. 140 * * α V V ∂ ∂ E E Γ V x c =0.1 V 120 Γ = V B C ≈ * V mol T E ∂ V p 100 x = 0.0 80 bulk modulus measured at T = 10 K 60 x = 0.15 40 40 Γ → ∞ ⇒ * 0 → E 20 T N V x = 0.3 0 AF AF x = 0.5 -20 0.01 0.1 1 10 x T (K) T (K) The non-Fermi liquid behavior is caused by a QCP.

Non-Fermi liquid behavior Fermi liquid for T → 0: q C / T → γ = constant α V / T → ∂γ / ∂ p = constant C p / T C / T 60 60 α V / T x = 0.15 4 x = 0.1 (J/ mol K 2 ) (10 -6 K -2 ) x = 0.5 x = 0.3 x = 0.15 40 3 3 x = 0.1 0 1 20 2 x = 0.0 x = 0.0 x = 0.3 T N 0 1 x = 0.5 0.5 x AF AF 0 -20 0.1 1 0.1 1 4 x T (K) T (K) T (K) T (K) Non-Fermi liquid behavior next to the onset of AF order. thermal expansion measurements for x = 0, 0.3, 0.5 from A. de Visser et al.

Comparison with the specific heat C / T ( V , T = 0.1K) C p ( V , T = const. → 0) tracks the maximum of S at the QPC. S p p x 0.0 0.5 1.0 4 x , p = 0 T = 0.1K T x = 0 0 p > 0 0.0, p > 0 x V c 3 x = 0.1, p > 0 V C p /T x = 0.2, p > 0 (J/mol K 2 ) x = 0.3, p > 0 2 2 x = 0.0, α V x = 0.1, α V T N 1 1 x = 0 15 α x = 0.15, α V N x = 0.3, α V AF 0 412 412 416 416 420 420 424 424 428 428 x V (Å 3 ) ln( / ) for ∂ C T α p 0 V Γ = ≈ T → ∂ C p p p p

Sign change of the thermal expansion S x = 0.1 p p x 0.0 0.5 1.0 4 T = 0.1K ~ 1/ T coh T V c coherence temperature from 3 V C p /T resistivity measurements (J/mol K 2 ) 2 2 ρ T N 1 1 N AF T 0 412 412 416 416 420 420 424 424 428 428 x T coh ( T Kondo ) V (Å 3 ) dominated b the Kondo lattice state dominated by the Kondo-lattice state

Sign change of the thermal expansion Expected behavior next to the QCP: 60 α V / T x = 0.1 T < T N T > T N (10 -6 K -2 ) x = 0.15 40 − α V ( x < x c ) ≈ α V ( x > x c ) α ( x < x ) ≈ α ( x > x ) x = 0.3 20 x = 0.5 • no sign change of α V 0 at T N ( x = 0.15) -20 ⇒ S maximum not at x = 0.1 -40 • with decreasing x and T with decreasing x and T increasing "background" -60 0.1 1 4 ⇒ di disorder ? d ? T (K) 40 ⇒ additional QCP ? x = 0.15 -6 K -2 ) 30 α V / T (10 - 20 10 0 0 0.1 1 10 thermal expansion measurements for x = 0, 0.3, T (K) 0.5 from A. de Visser et al.

Disorder ? possible ibl α V / T - background 0 0 0.0 0 5 0.5 1 0 1.0 x For x < 0.3 all samples show: C ( x ) ≈ C ( p ) S Sample with the largest l ith th l t ⇒ no "background" visible chemical disorder p x 0.0 0.5 1.0 4 T = 0.1K 3 C p /T (J/mol K 2 ) 2 1 0 0 412 416 420 424 428 V (Å 3 )

Linear thermal expansion coefficients α a,b,c ( T > 10K) x = 0 x = 0.1 x = 0.15 x = 0.3 x = 1.0 α a,b,c (4f) 10 (10 -6 K -2 ) c (10 6 K 2 ) c c c c c c 5 a a a a a a a 0 a c c c c -5 5 ∆ CEF (meV) ( V) ∆ c 0 – 7 – 13.8 0 – 8.6 – 13.8 10 100 10 100 10 100 10 100 10 100 T (K) T (K) T (K) T (K) T (K) T (K) T (K) T (K) T (K) T (K) Cu Distortion of the lattice due to CEF splitting of the 4f state. T c c Ce b ∆ CEF from Stroka et al. b