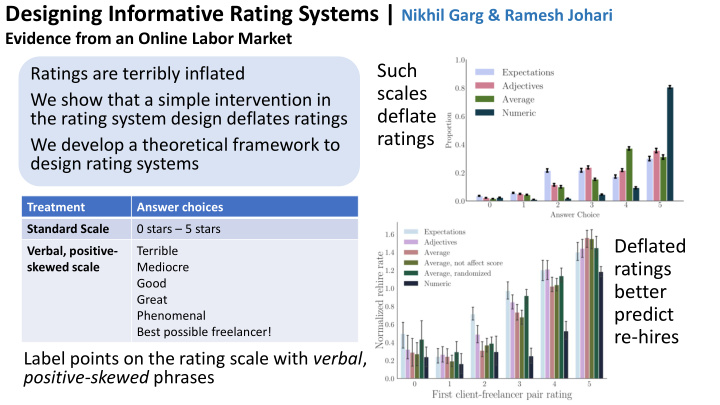
Theoretical approach Suppose we have estimated a joint distribution - - PowerPoint PPT Presentation

β–Ά
theoretical approach
SMART_READER_LITE
LIVE PREVIEW

Theoretical approach Suppose we have estimated a joint distribution - - PowerPoint PPT Presentation

Apr 06, 2023 472 likes β€’531 views

Designing Informative Rating Systems | Nikhil Garg & Ramesh Johari Evidence from an Online Labor Market Such Ratings are terribly inflated scales We show that a simple intervention in deflate the rating system design deflates ratings

slide-1
SLIDE 1

Designing Informative Rating Systems | Nikhil Garg & Ramesh Johari

Evidence from an Online Labor Market

Ratings are terribly inflated We show that a simple intervention in the rating system design deflates ratings We develop a theoretical framework to design rating systems Label points on the rating scale with verbal, positive-skewed phrases

Treatment Answer choices Standard Scale 0 stars – 5 stars Verbal, positive- skewed scale Terrible Mediocre Good Great Phenomenal Best possible freelancer!

Such scales deflate ratings Deflated ratings better predict re-hires

slide-2
SLIDE 2

Theoretical approach

Suppose we have estimated a joint distribution between seller quality and the ratings the receive, ො 𝜍(y , πœ„) = ΰ·’ Pr y| መ πœ„ , for each possible rating scale Under our (stylized) model…

  • Sellers accumulate ratings according to 𝜍
  • Platform estimates ranking by empirical rating average
  • Estimated ranking converges to true ranking, at a large

deviations rate that depends on 𝜍

slide-3
SLIDE 3

Experiment: How does platform design affect response distributions? Theory: How does the response distribution affect learning?

Platform Design Information Platform Objective

Question asked Answer distribution Learning about participants Truth Estimated

Errork β‰ˆ π‘“βˆ’π‘™π›Ώ π‘’π‘“π‘‘π‘—π‘•π‘œ

Rate 𝛿 π‘’π‘“π‘‘π‘—π‘•π‘œ at which platform recovers truth can be calculated after an experiment

More generally, a framework for designing the information received from platform participants.

Designing Informative Rating Systems: Evidence from an Online Labor Market [w/ R. Johari] Designing Optimal Binary Rating Systems [w/ R. Johari] Who is in Your Top Three? Optimizing Learning in Elections with Many Candidates [w/ L. Gelauff, S. Sakshuwong, A. Goel]

slide-4
SLIDE 4

Optimal systems with various platform goals

  • In a follow-up paper in AISTATS*, we
  • Develop a non-convex optimization algorithm to

find the optimal system

  • Show how information goals should be

incorporated into design

  • In the above example, inflated ratings are
  • ptimal

*Designing Optimal Binary Rating Systems

Suppose a (commodity-heavy) marketplace primarily wants to separate the bottom 5% of sellers from everyone else. What rating system should it use?