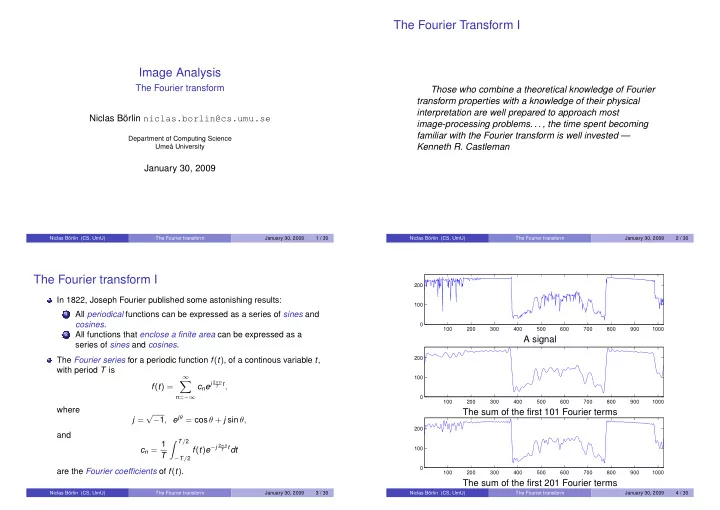
The Fourier Transform I Image Analysis The Fourier transform Those - PowerPoint PPT Presentation

The Fourier Transform I Image Analysis The Fourier transform Those who combine a theoretical knowledge of Fourier transform properties with a knowledge of their physical interpretation are well prepared to approach most Niclas Börlin niclas.borlin@cs.umu.se image-processing problems. . . , the time spent becoming familiar with the Fourier transform is well invested — Department of Computing Science Kenneth R. Castleman Umeå University January 30, 2009 Niclas Börlin (CS, UmU) The Fourier transform January 30, 2009 1 / 30 Niclas Börlin (CS, UmU) The Fourier transform January 30, 2009 2 / 30 The Fourier transform I 200 In 1822, Joseph Fourier published some astonishing results: 100 All periodical functions can be expressed as a series of sines and 1 0 cosines . 100 200 300 400 500 600 700 800 900 1000 All functions that enclose a finite area can be expressed as a 2 A signal series of sines and cosines . 200 The Fourier series for a periodic function f ( t ) , of a continous variable t , with period T is 100 ∞ � c n e j 2 π n T t , f ( t ) = 0 n = −∞ 100 200 300 400 500 600 700 800 900 1000 where The sum of the first 101 Fourier terms √ − 1 , e j θ = cos θ + j sin θ, j = 200 and � T / 2 c n = 1 f ( t ) e − j 2 π n T t dt 100 T − T / 2 0 are the Fourier coefficients of f ( t ) . 100 200 300 400 500 600 700 800 900 1000 The sum of the first 201 Fourier terms Niclas Börlin (CS, UmU) The Fourier transform January 30, 2009 3 / 30 Niclas Börlin (CS, UmU) The Fourier transform January 30, 2009 4 / 30

The Fourier transform The Fourier transform of a Gaussian Given f ( t ) = e − π t 2 we have � ∞ � ∞ The continuous Fourier transform of a complex-valued function e − π t 2 e − j 2 π st dt = e − π ( t 2 + jst ) dt . F ( s ) = f ( t ) is defined as −∞ −∞ � ∞ Multiply the right hand side by e − π s 2 e π s 2 : f ( t ) e − j 2 π st dt . F{ f ( t ) } = F ( s ) = −∞ F ( s ) = e − π s 2 � ∞ e π s 2 e − π ( t 2 + jst ) dt Its inverse is defined as −∞ = e − π s 2 � ∞ � ∞ e − π ( t 2 + jst − s 2 ) dt F − 1 { F ( s ) } = f ( t ) = F ( s ) e j 2 π st ds . −∞ −∞ = e − π s 2 � ∞ e − π ( t + js ) 2 dt The Fourier transform for a function is unique. −∞ = e − π s 2 � ∞ The functions f ( t ) and F ( s ) are called a Fourier transform pair . e − π u 2 du = e − π s 2 . −∞ Thus the Fourier transform of a Gaussian is another Gaussian. Niclas Börlin (CS, UmU) The Fourier transform January 30, 2009 5 / 30 Niclas Börlin (CS, UmU) The Fourier transform January 30, 2009 6 / 30 When does the Fourier transform exist? The spatial domain vs. the frequency domain The Fourier transform does not exist for all functions. From the Euler formula However, the Fourier transform always exists if e j θ = cos θ + j sin θ � ∞ | f ( t ) | dt < ∞ −∞ we see that all functions with a well-defined Fourier transform can be re-written as a sum of sines and cosines of different and f ( t ) is continuous or f ( t ) has a finite number of frequencies. discontinuities. This is why we say that the Fourier transform takes us from the Such a function is called transient . spatial domain (or the time domain ) to the frequency domain . Thus, the Fourier transform exists for all signals (images) that are possible to represent in a computer! Niclas Börlin (CS, UmU) The Fourier transform January 30, 2009 7 / 30 Niclas Börlin (CS, UmU) The Fourier transform January 30, 2009 8 / 30

Properties of complex functions Impulses In general, the Fourier transform of a real function is complex. A Unit impulse of a continous variable t located at t = 0, is defined as A complex function F ( u ) = R ( u ) + jI ( u ) may be expressed as � ∞ if t = 0 δ ( t ) = otherwise . F ( u ) = | F ( u ) | e − j φ ( u ) , 0 where � R 2 ( u ) + I 2 ( u ) , | F ( u ) | = is known as the spectrum and φ ( u ) = tan − 1 I ( u ) Furthermore, δ ( t ) satisfies R ( u ) � ∞ δ ( t ) dt = 1 . is known as the phase angle . −∞ The Power spectrum or Power spectral density is defined as The unit impulse δ ( t ) is called the Dirac Delta function , even P ( u ) = | F ( u ) | 2 . though it is not a proper function. Niclas Börlin (CS, UmU) The Fourier transform January 30, 2009 9 / 30 Niclas Börlin (CS, UmU) The Fourier transform January 30, 2009 10 / 30 Sifting Impulse train — the Shah function The Dirac delta has the following important sifting property � ∞ An Impulse train is a sum of infinitely many periodic impulses f ( t ) δ ( t ) dt = f ( 0 ) ∆ T apart −∞ ∞ � s ∆ T ( t ) = δ ( t − n ∆ T ) . or � ∞ n = −∞ f ( t ) δ ( t − t 0 ) dt = f ( t 0 ) , −∞ assuming that f ( t ) is continous at t 0 . This means that � ∞ δ ( t − t 0 ) e − j 2 π st dt = e − j 2 π st 0 F{ δ ( t − t 0 ) } = The expression s ∆ T ( t ) is sometimes called the Shah function or −∞ sampling function . and We will use impulse trains later during sampling. � ∞ δ ( t − t 0 ) e − j 2 π st dt = e − j 2 π s 0 = 1 . F{ δ ( t − 0 ) } = −∞ Niclas Börlin (CS, UmU) The Fourier transform January 30, 2009 11 / 30 Niclas Börlin (CS, UmU) The Fourier transform January 30, 2009 12 / 30

The box and sinc functions The symmetry of the Fourier transform Another function important for sampling is the box function � A The forward and inverse Fourier transforms differs by only the if | t | ≤ W / 2 f ( t ) = sign of the exponential. 0 otherwise Thus, if whith its fourier transform F ( s ) = F{ f ( t ) } , F ( s ) = AW sin ( π sW ) = AW sinc ( sW ) , then π sW F{ F ( t ) } = f ( − s ) . where the sinc function is defined as sinc ( x ) = sin π x For example, if f ( t ) is the box function and . π x F ( s ) = F{ f ( t ) } = AW sinc ( sW ) , then F{ F ( s ) } = F{ AW sinc ( sW ) } = f ( − s ) . Thus, the Fourier transform of a box function is a sinc function, and vice versa. Niclas Börlin (CS, UmU) The Fourier transform January 30, 2009 13 / 30 Niclas Börlin (CS, UmU) The Fourier transform January 30, 2009 14 / 30 Three box functions and their Fourier transforms Some useful theorems The Addition theorem : For two functions f ( t ) and g ( t ) , F{ f ( t ) + g ( t ) } = F{ f ( t ) } + F{ g ( t ) } = F ( s ) + G ( s ) . The Shift theorem : If a function f ( t ) is shifted an amount a , then F{ f ( t − a ) } = e − j 2 π as F ( s ) . The Similarity theorem : For a function f ( t ) with Fourier transform F ( s ) , F{ f ( at ) } = 1 | a | F ( s / a ) . f ( x ) | F ( u ) | Thus, if the function is compressed in one domain it is expanded in the other. Niclas Börlin (CS, UmU) The Fourier transform January 30, 2009 15 / 30 Niclas Börlin (CS, UmU) The Fourier transform January 30, 2009 16 / 30

The Fourier transform of the Shah function The Fourier transform of the Shah function The interval [ − ∆ T / 2 , ∆ T / 2 ] contains only the impulse at the The Shah function is periodic with period ∆ T origin. Thus, ∞ � s ∆ T ( t ) = δ ( t − n ∆ T ) . � ∆ T / 2 1 1 1 ∆ T e 0 = δ ( t ) e − j 2 π n n = −∞ ∆ T t dt = c n = ∆ T . ∆ T − ∆ T / 2 Thus it can be written as a Fourier series and ∞ ∞ � c n e j 2 π n 1 � ∆ T t , e j 2 π n s ∆ T ( t ) = ∆ T t . s ∆ T ( t ) = ∆ T n = −∞ n = −∞ We want to find where � ∆ T / 2 1 s ∆ T ( t ) e − j 2 π n ∆ T t dt . c n = ∞ 1 � F{ e j 2 π n ∆ T ∆ T t } . F{ s ∆ T ( t ) } = − ∆ T / 2 ∆ T n = −∞ Niclas Börlin (CS, UmU) The Fourier transform January 30, 2009 17 / 30 Niclas Börlin (CS, UmU) The Fourier transform January 30, 2009 18 / 30 The Fourier transform of the Shah function Convolution and the Convolution theorem We know that The convolution of two continous functions f ( t ) and h ( t ) is F{ δ ( t − t 0 ) } = e − j 2 π st 0 . defined as � ∞ f ( t ) ⋆ h ( t ) = f ( τ ) h ( t − τ ) d τ. Thus, by symmetry −∞ F{ e − j 2 π tt 0 } = δ ( − s − t 0 ) . The Fourier transform of the convolution is � ∞ �� ∞ � Substituting − t 0 = n / ∆ T we find that e − j 2 π st dt F{ f ( t ) ⋆ h ( t ) } = f ( τ ) h ( t − τ ) d τ −∞ −∞ � ∞ �� ∞ F{ e j 2 π n � ∆ T t } = δ ( − s + n / ∆ T ) = δ ( n / ∆ T − s ) = δ ( s − n / ∆ T ) . h ( t − τ ) e − j 2 π st dt = f ( τ ) d τ −∞ −∞ Thus, � �� � ∞ F{ h ( t − τ ) } = H ( s ) e − j 2 π st 1 � � ∞ F{ s ∆ T ( t ) } = δ ( s − n / ∆ T ) . ∆ T f ( τ ) e − j 2 π st d τ = H ( s ) n = −∞ −∞ In other words, the Fourier transform of an impulse train with = H ( s ) F ( s ) . period ∆ T is another impulse train with period 1 / ∆ T. Niclas Börlin (CS, UmU) The Fourier transform January 30, 2009 19 / 30 Niclas Börlin (CS, UmU) The Fourier transform January 30, 2009 20 / 30