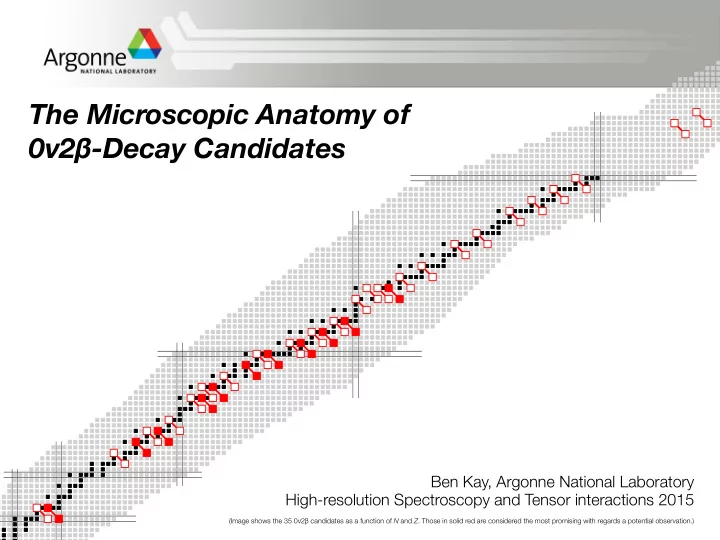

The Microscopic Anatomy of 0 ν 2 β -Decay Candidates Ben Kay, Argonne National Laboratory High-resolution Spectroscopy and Tensor interactions 2015 (Image shows the 35 0 ν 2 β candidates as a function of N and Z . Those in solid red are considered the most promising with regards a potential observation.)
Overview • A brief introduction - double beta decay, the candidates, nuclear matrix elements, transfer reactions • The 76 Ge ➞ 76 Se system (work from 2008 and 2009, a recap) - results and impact • The 130 Te ➞ 130 Xe and 136 Xe ➞ 136 Ba systems (2013 and 2015) RCNP - Overview of the landscape - Existing data on the neutron vacancies for the A = 130 system - New data on the proton occupancies for A = 130 and 136 - New data on the neutron occupancies for A = 136 • Comparison with available calculations - Detailed comparisons with recent results from the CMU group (2015) • Outlook and conclusions - Moving towards complete data sets for key isotopes including the 100 Mo ➞ 100 Ru and 150 Nd ➞ 150 Sm systems RCNP - Data soon to be available for the 82 Se ➞ 82 Kr system - Summary General discussions on this topic: S. J. Freeman and J. P . Schi ff er, J. Phys. G: Nucl. Part. Phys. 39 , 124004 ( 2012 ) 2
Beta decay, double beta decay 67020 70740 121025 A = 72 A = 76 A = 130 (~74% of isobars) odd-odd 67015 70735 121020 76 Rb even-even 72 Ni 72 Kr 130 Ce β – 76 Zn β +, ε ε Mass (MeV) 67010 70730 121015 72 Br 130 Sn β – 130 La 72 Cu β – 130 Sb 76 Ga β – β – 67005 70725 76 Br 121010 ε 76 Kr 130 I 130 Cs β +, ε ε ✕ β – ✕ 130 Te 76 As β – ✕ β – 76 Ge 130 Ba β – β – 72 As β +, ε 72 Ga β + β +, εε 67000 72 Se 70720 121005 β – β – ε 72 Zn 2.527 MeV* 130 Xe ε 76 Se 2.039 MeV* 72 Ge 66995 70715 121000 28 30 32 34 36 38 28 30 32 34 36 38 48 50 52 54 56 58 Z Z Z Pairing in nuclei results in a displacement of even-even and odd-odd mass parabolas for given isobars. Data from AME 2012. Precise masses ⇒ precise Q value. 1 / 2 ] − 1 = (Phase Space Factor) ⇥ | Nuclear Matrix Element | 2 ⇥ | h m ββ i | 2 [ T 0 ν 3
Double beta decay Elucidating the nature of neutrinos is ν α one of the major challenges to m 2 m 2 contemporary science — ν e 3 X m i U 2 m ββ = ν µ α i • Majorana or Dirac? n =1 ν τ • Lepton number conservation? • Absolute mass scale? 2 2 m 3 m 2 solar~7 × 10 − 5 eV 2 • Mass mechanisms? 2 m 1 • Matter-antimatter asymmetry? atmospheric ~2 × 10 − 3 eV 2 • … atmospheric Δ m 122 ~2 × 10 − 3 eV 2 2 m 2 Δ m 132 solar~7 × 10 − 5 eV 2 Normal Ordering with uncertainty 2 2 m 1 m 3 Inverted Ordering with uncertainty Normal Ordering without uncertainty 10 0 Inverted Ordering without uncertainty ? ? m 0 νββ [eV] 95% CL, Planck+WMAP+highL+BAO KamLAND-Zen + EXO 200 0 0 10 -1 95% CL, Planck+WMAP+highL From King et al., Rep. Prog. Phys. 76, 056201 (2013) Figure 1. The probability that a particular neutrino mass state 10 -2 10 -3 10 -4 10 -4 10 -3 10 -2 10 -1 10 0 http://ctp.berkeley.edu/neutrino/neutrino5.html m 0 [eV] 1 / 2 ] − 1 = (Phase Space Factor) ⇥ | Nuclear Matrix Element | 2 ⇥ | h m ββ i | 2 [ T 0 ν 4
Double beta decay on the Segré chart Which isotopes are candidates? What are the best candidates? Sn Z Ni Ca N 1 / 2 ] − 1 = (Phase Space Factor) ⇥ | Nuclear Matrix Element | 2 ⇥ | h m ββ i | 2 [ T 0 ν 5
Double beta decay on the Segré chart Which isotopes are candidates? What are the best candidates? Moving in the β – direction there are 35 double- β -decay candidates, with Q values ranging from 0.1-4.3 MeV, with natural abundances of 0.004-35%*. Sn Z Ni Figure of 2 β – spectrum from Elliott and Vogel, Annu. Rev. Nucl. Part. Sci. 52 , 115 (2002) Ca *Excluding the alpha emitters ( 232 Th and 238 U, which are ~100%) For 11 of these, the 2 ν mode has been observed. N Also, 2v mode to excited 0 + states seen in 100 Mo and 150 Nd. 1 / 2 ] − 1 = (Phase Space Factor) ⇥ | Nuclear Matrix Element | 2 ⇥ | h m ββ i | 2 [ T 0 ν 6
Double beta decay on the Segré chart Which isotopes are candidates? What are the best candidates? A large Q value (greater than 2 MeV) is desired because puts the signal above background from natural radioactivity. Additionally, the decay probability scales with ~Q 5 . The rest is a compromise between natural abundance, detector technology, economics, and nuclear structure 150 Nd 82 Se 4 48 Ca 96 Zr 100 Mo 3 130 Te Sn 136 Xe 116 Cd 124 Sn 110 Pd 2 76 Ge 1 Q 2 β – (MeV) Z 0.5 0.3 0.2 Ni 0.1 Ca N 0.01 0.1 1 10 100 Natural abundance (%) 1 / 2 ] − 1 = (Phase Space Factor) ⇥ | Nuclear Matrix Element | 2 ⇥ | h m ββ i | 2 [ T 0 ν 7
Nuclear matrix elements (uncertainties here) Magnitude of NME (dimensionless) Figure: A. Neacsu and M. Horoi, Phys. Rev. C 91 , 024309 (2015) Tremendous e ff orts have been put into the exploration of what may remedy this uncertainty. Our focus is on experimental nuclear-structure data to constrain the calculations. 1 / 2 ] − 1 = (Phase Space Factor) ⇥ | Nuclear Matrix Element | 2 ⇥ | h m ββ i | 2 [ T 0 ν 8
NMEs for 2 ν 2 β reasonably well established What experimentally accessible nuclear-structure properties can be useful? First a look at the process … and start with what is known (and observed) in 2v2 β 2v2 β Dominated by Gamow-Teller transitions via 1 + states in the Dominated by GT transitions via 1 + intermediate nucleus, confined to states in the intermediate nucleus. low excitation energy Nuclear structure e ff ects key T = 6 0 + ias (excitation energy and strength of 1 + T = 6 E states) AND can be probed T = 5 0 + das experimentally via charge exchange reactions e.g.: 76 Ge( 3 He,t) 76 As, 76 Se(t, 3 He) 76 As. 76 As 0 + g.s. T = 6 0 + g.s. 76 Ge T = 4 76 Se 9
NMEs for 0 ν 2 β less so What experimentally accessible nuclear-structure properties can be useful? Not quite so straight forward with 0v2 β ( Mediation by a virtual neutrino 0v2 β gives di ff erent features: ) Probes all intermediate states up to 10s of MeV, any spin, up to 5 to 6h Energy of intermediate states can be large, 10’s of MeV cf. a few for 2v2 β … Angular momentum can be large, 5-6 hbar cf. 1 hbar for 2v2 β So … it probes essentially all states, and is somewhat insensitive to the E details … closure approximation used* Not related to 2v2 β , so no short cuts. 76 As No obvious probes that connect the 0 + g.s. T=6 initial and final ground states e.g., 0 + g.s. 76 Ge T=4 76 Ge( 18 Ne, 18 O) 76 Se. 76 Se *Often considered good to 10% or better, see e.g., Sen’kov and Horoi, Phys. Rev. C 90 , 051301(R) ( 2014 ) 10
The 76 Ge ➞ 76 Se system (a recap) Z 0 g 7/2 50 0 g 9/2 1 p 1/2 0 f 5/2 1 p 3/2 28 0 f 7/2 8 14 34 32 16 6 28 N 28 42 44 50 What is the occupancy and vacancy of the active orbitals? How does it CHANGE from initial to final state? —the MICROSCOPIC anatomy can be probed with NUCLEON TRANSFER reactions. 11
Tools of the trade — transfer reactions A well-understood probe of nuclear structure, much of the formalism developed in the late 50s / early 60s. Exploited to great e ff ect, and recently reevaluated extensively. 0 g 7/2 Approach 50 • Careful choice of reactions for 0 g 9/2 adding and removing protons and 1 p 1/2 neutrons 0 f 5/2 • Consistent experimental 1 p 3/2 28 approaches 0 f 7/2 • Consistent analyses (DWBA) The facilities 1600 1 • MLL Munich (tandem, Q3D) 4 • IPN Orsay (tandem, Enge split 1200 76 Se(p,d) pole) Co u nts 76 Se( 3 He, α ) 800 • RCNP Osaka (cyclotron, Grand Raiden) 400 3 • WNSL Yale (tandem, Enge split 2 1 2 3 pole) 0 -0.2 0 0.2 0.4 0.6 0.8 1 Excitation Ener g y (MeV) 12
Sum rules, normalization (cross sections ➞ occupancy) 76 Ge( p , d ) 76 Ge( d , p ) E ℓ S’ S E ℓ (2 j +1) S ’ (2 j +1) S 0 1 0.45 0.85 160 1 0.44 0.82 191 4 225 4 248 1 0.12 0.23 421 2 317 3 505 2 457 3 629 1 0.15 0.28 575 1 1.29 2.43 884 2 651 3 1021 1 0.12 0.22 885 1 0.10 0.19 1048 1 0.04 0.07 1137 1 0.11 0.21 1250 0 1250 3 1385 2 1410 0 1451 1 0.37 0.70 1580 3 N j ≡ S 0 /S X X S 0 (2 j + 1) S 0 N j ≡ [ removing + adding ] / (2 j + 1) N j ≡ [(0 . 45 + 0 . 12 + 1 . 29 + 0 . 10 + 0 . 11 + 0 . 37) + (0 . 44 + 0 . 15 + 0 . 12 + 0 . 04)] / (2 + 4) = 0 . 53 The value of this normalization is not arbitrary (reflects quenching of single-particle motion). Normalizing is essential compare experiment data to calculations. 13
A look back at the Ge/Se results ( WNSL Yale, 2006/7, RCNP 2007 ) N = 42 N = 44 0 g 9/2 EXP EXP e.g., Neutron occupancies 1 p 76 Ge 76 Se Neutron vancancy 0 f 5/2 8 8 Isotope 0 f 5/2 1 p 1/2,3/2 0 g 9/2 Sum Expect 0 ν 2 β 6 6 74 Ge 1.8(4) 1.1(2) 4.3(3) 7.2(5) 8 4 4 2 2 76 Ge 1.4(3) 1.1(2) 3.5(2) 6.0(5) 6 0 0 76 Se 2.2(3) 1.6(2) 4.2(2) 8.0(5) 8 EXP EXP 76 Ge 76 Se 78 Se 2.3(4) 0.9(2) 2.8(3) 6.1(5) 6 8 8 Proton occupancy 0 ν 2 β (E292) 6 6 The ( d , p ) and ( p , d ) reactions used for the 1 p 4 4 strength and the ( α , 3 He)+( 3 He, α ) used for the 0 f 5/2 and 0 g 9/2 . 2 2 A similar table can be made for the proton 0 0 Z = 32 Z = 34 occupancies. J. P . Schi ff er et al ., Phys. Rev. Lett. 100 , 112501 ( 2008 ); BPK et al ., Phys. Rev. C 79 , 021301(R) ( 2009 ) 14
Recommend
More recommend