


The inert doublet model of dark matter revisited H 0 W m h = 120 GeV, ∆ m H + = 50 GeV 0.1 0.01 λ L W ¯ f ′ 3-body, ∆ m A 0 =10 GeV 2-body , ∆ m A 0 =10 GeV 3-body, ∆ m A H 0 0 =50 GeV 0.001 f 2-body , ∆ m A 0 =50 GeV 60 65 70 75 80 m H 0 [GeV] Based on Phys.Rev.D81:075024,2010, arXiv:1003.3125 (with Laura Lopez), and work in progress. Carlos E. Yaguna UAM and IFT 2010
In the inert doublet model (IDM) the SM is extended with a second higgs doublet H + � � The idm contains 3 √ H 2 = ( H 0 + iA 0 ) / 2 new scalars H 2 is odd under a new Lightest component is stable Z 2 symmetry No coupling to fermions Barbieri, Bergstrom, Gustaffson, This model features a Ma, Tytgat, etc rich phenomenology
The inert doublet model can account for the dark matter of the Universe It includes a viable The lightest odd particle: H 0 dm candidate H 0 has gauge and 1 | H 1 | 2 + µ 2 2 | + λ 1 | H 1 | 4 + λ 2 | H 2 | 4 V = µ 2 2 | H 2 scalar interactions + λ 3 | H 1 | 2 | H 2 | 2 + λ 4 | H † 1 H 2 | 2 � � 1 H 2 ) 2 + h . c . ( H † + λ 5 2 m H 0 , m A 0 , m H ± The parameter space is rather simple λ L ≡ 1 2 ( λ 3 + λ 4 + λ 5 )
Dark matter annihilations might be dominated by three-body final states such as W W ∗ or t ¯ t ∗ A new effect not included Yaguna (2010), Kamionkowski (1998) in most analysis nor in DarkSUSY or micrOMEGAs They affect Ω dm and the modifying the viable parameter space dm detection prospects H 0 H 0 may annihilate into for m H 0 < M W W W ∗ in the IDM
In the IDM the viable parameter space coincides with the region where H 0 H 0 → W W ∗ is important H 0 H 0 → W + W − has a ∝ g 2 purely gauge contribution The viable parameter space is m H 0 < M W or m H 0 > 500 GeV In that region, b ¯ b is the dominant 2-b final state
Three different diagrams contribute to f ′ in the IDM H 0 H 0 → W W ∗ → W f ¯ H 0 W H 0 W ∝ g 3 There are two gauge H ± f ′ ¯ W ¯ f ′ diagrams W H 0 H 0 f f H 0 W ∝ g 2 λ L And a higgs mediated h f diagram W H 0 f ′ ¯ Coannihilations may also affect Ω
In the IDM, the three-body annihilation rate can be much larger than the two-body one This effect depends on 10000 the higgs mass m h = 120 GeV m h = 150 GeV m h = 200 GeV 100 * )/ σ (2-body) The correct σ could be 100 times larger 1 σ (WW λ L = 1e-2 0.01 ∆ m A 0 = ∆ m H + = 50 GeV σ (3 -body ) > σ (2 -body ) over a wide m H 0 range 70 80 50 60 m H 0 (GeV)
The H 0 relic density is strongly reduced by annihilations into W W ∗ A significant effect 1 independently of m h m h = 120 GeV m h = 150 GeV m h = 200 GeV 0.8 Ω (2- +3-body)/ Ω (2-body) 0.6 Ω could be more than 10 times smaller 0.4 0.2 λ L = 1e-2 This is a generic feature ∆ m H + = 50 GeV 0 50 60 70 80 of the IDM m H 0 (GeV)
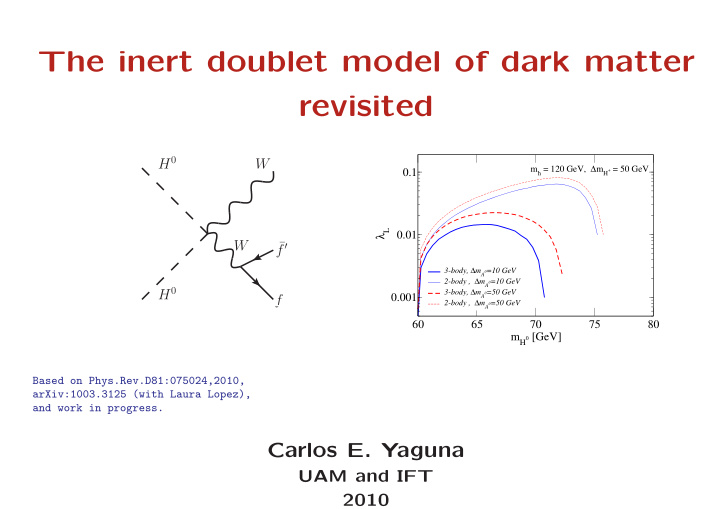
Due to 3-body final states, the viable parameter space of the IDM is substantially modified The required value of λ L may be much smaller m h = 120 GeV, ∆ m H + = 50 GeV 0.1 The maximum allowed 0.01 λ L m H 0 decreases 3-body, ∆ m A 0 =10 GeV 2-body , ∆ m A 0 =10 GeV 3-body, ∆ m A 0 =50 GeV 0.001 2-body , ∆ m A 0 =50 GeV Similar results for other 60 65 70 75 80 parameters m H 0 [GeV]
The inert higgs direct detection cross section is much smaller than previously believed The dd cross section is proportional to λ 2 m h = 120 GeV , ∆ m H + = 50 GeV 1e-07 L CDMS 2009 1e-08 0 -N [pb] The new σ H 0 - N is up to 1e-09 100 times smaller σ H 3-body, ∆ m A 0 = 10 GeV 1e-10 2-body, ∆ m A 0 = 10 GeV 3-body, ∆ m A 0 =50 GeV 2-body, ∆ m A 0 = 50 GeV Indirect detection signals 1e-11 60 65 70 75 80 are also affected m H 0 [GeV]
The 3-body final state W W ∗ plays a major role in the dm phenomenology of the IDM H 0 W They modify the viable parameter space W f ′ ¯ H 0 f They alter the dm detection prospects 10000 m h = 120 GeV, ∆ m H + = 50 GeV 0.1 m h = 120 GeV m h = 150 GeV m h = 200 GeV 100 * )/ σ (2-body) 0.01 λ L 1 σ (WW 3-body, ∆ m A 0 =10 GeV They induce large 2-body , ∆ m A 0 =10 GeV 3-body, ∆ m A 0 =50 GeV 0.001 0.01 λ L = 1e-2 2-body , ∆ m A 0 =50 GeV ∆ m A 0 = ∆ m H + = 50 GeV corrections 60 65 70 75 80 60 70 80 50 m H 0 [GeV] m H 0 (GeV)
Recommend
More recommend