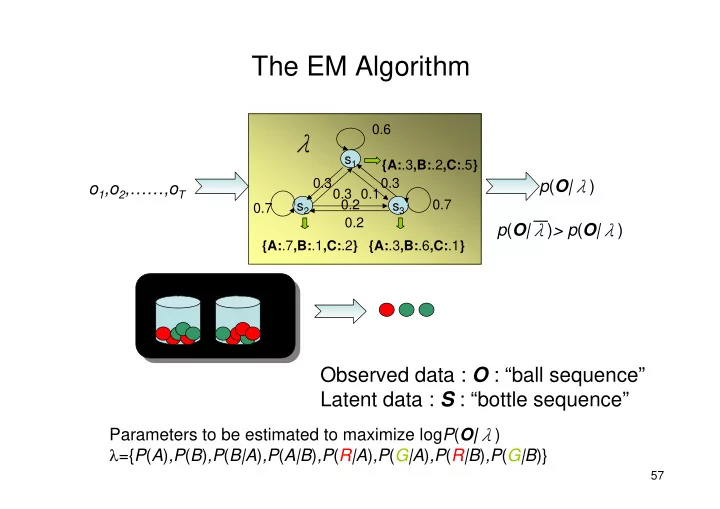
The EM Algorithm 0.6 s 1 {A: .3 ,B: .2 ,C: .5 } 0.30.3 0.20.10.3 - PowerPoint PPT Presentation

The EM Algorithm 0.6 λ s 1 {A: .3 ,B: .2 ,C: .5 } 0.30.3 0.20.10.3 p ( O | λ ) o 1 ,o 2 ,……,o T 0.7 s 2 s 3 0.7 0.2 p ( O | λ ) > p ( O | λ ) {A: .7 ,B: .1 ,C: .2 } {A: .3 ,B: .6 ,C: .1 } A B Observed data : O : “ball sequence” Latent data : S : “bottle sequence” Parameters to be estimated to maximize log P ( O| λ ) λ ={ P ( A ) ,P ( B ) ,P ( B|A ) ,P ( A|B ) ,P ( R|A ) ,P ( G|A ) ,P ( R|B ) ,P ( G|B )} 57

The EM Algorithm • Introduction of EM (Expectation Maximization): – Why EM? • Simple optimization algorithms for likelihood function relies on the intermediate variables, called latent ( 隱藏的 )data In our case here , the state sequence is the latent data • Direct access to the data necessary to estimate the parameters is impossible or difficult In our case here, it is almost impossible to estimate { A , B , π } without consideration of the state sequence – Two Major Steps : • E : expectation with respect to the latent data using the current estimate of the parameters and conditioned on the [ ] • E S λ O , observations • M : provides a new estimation of the parameters according to Maximum likelihood (ML) or Maximum A Posterior (MAP) Criteria 58

The EM Algorithm ML and MAP • Estimation principle based on observations: ( ) { } = = x x x x X X , X ,..., X , ,..., n 1 2 1 2 n – The Maximum Likelihood (ML) Principle ( ) p x Φ Φ find the model parameter so that the likelihood is maximum { } = Φ µ Σ for example, if is the parameters of a multivariate , normal distribution, and X is i.i.d. ( independent, identically { } distributed ) , then the ML estimate of = Φ µ Σ is , ( )( ) 1 1 n n t = = − − µ x Σ x µ x µ ∑ ∑ , ML i ML i ML i ML n n = = i i 1 1 – The Maximum A Posteriori (MAP) Principle ( ) p Φ x Φ find the model parameter so that the likelihood is maximum 59

The EM Algorithm • The EM Algorithm is important to HMMs and other learning techniques – Discover new model parameters to maximize the log-likelihood ( ) P O λ of incomplete data by iteratively maximizing the log ( ) log P O , S λ expectation of log-likelihood from complete data • Using scalar random variables to introduce the EM algorithm O – The observable training data ( ) λ P O λ • We want to maximize , is a parameter vector S – The hidden (unobservable) data O • E.g. the component densities of observable data , or the underlying state sequence in HMMs 60

The EM Algorithm λ S – Assume we have and estimate the probability that each O occurred in the generation of ( ) O , S – Pretend we had in fact observed a complete data pair with ( ) P O , S λ frequency proportional to the probability , to λ λ computed a new , the maximum likelihood estimate of – Does the process converge? unknown model setting – Algorithm ( ) ( ) ( ) = Bayes’ rule P O S λ P S O λ P O λ , , incomplete data likelihood complete data likelihood • Log-likelihood expression and expectation taken over S ( ) ( ) ( ) = − P O λ P O S λ P S O λ log log , log , take expectation over S [ ] ( ) ( ) ( ) ∑ = P O λ P S O λ P O λ log , log s [ ] [ ] ( ) ( ) ( ) ( ) ∑ ∑ = − P S O λ P O S λ P S O λ P S O λ , log , , log , 61 S S

The EM Algorithm – Algorithm (Cont.) ( ) P O λ • We can thus express as follows log ( ) P O λ log [ ] [ ] ( ) ( ) ( ) ( ) ∑ ∑ = − P S O λ P O S λ P S O λ P S O λ , log , , log , S S ( ) ( ) = − Q λ λ H λ λ , , where [ ] ( ) ( ) ( ) ∑ = Q λ λ P S O λ P O S λ , , log , S [ ] ( ) ( ) ( ) ∑ = H λ λ P S O λ P S O λ , , log , S ( ) ( ) ≥ P O λ P O λ • We want log log ( ) ( ) − P O λ P O λ log log [ ] ( ) ( ) [ ] ( ) ( ) = − − − Q λ λ H λ λ Q λ λ H λ λ , , , , ( ) ( ) ( ) ( ) = − − + Q λ λ Q λ λ H λ λ H λ λ , , , , 62

The EM Algorithm ( ) ( ) − + H λ , λ H λ , λ • has the following property ( ) ( ) − + H λ λ H λ λ , , ( ) Kullbuack-Leibler (KL) distance ⎡ ⎤ P S O λ ( ) , ∑ = − ⎢ ⎥ P S O λ ( ) , log P S O λ ⎢ ⎥ , ⎣ ⎦ S ( ) ⎡ ⎤ ⎛ ⎞ P S O λ ( ) , ⎜ ⎟ ∑ ⎢ ⎥ ≥ − ≤ − P S O λ x x Jensen’s inequality Q ( ) , 1 ( log 1 ) ⎜ ⎟ ⎢ P S O λ ⎥ , ⎝ ⎠ ⎣ ⎦ S [ ] ( ) ( ) ∑ = − P S O λ P S O λ , , S = 0 ( ) ( ) ∴ − + ≥ H λ λ H λ λ , , 0 ( ) P O λ – Therefore, for maximizing , we only need to log maximize the Q -function (auxiliary function) [ ] ( ) ( ) ( ) Expectation of the complete ∑ = Q λ λ P S O λ P O S λ , , log , data log likelihood with respect to the latent state sequences S 63

EM Applied to Discrete HMM Training • Apply EM algorithm to iteratively refine the HMM λ = A B π ( , , ) parameter vector – By maximizing the auxiliary function [ ] ( ) ( ) ( ) = Q λ , λ P S O , λ log P O , S λ ∑ S ( ) ⎡ ⎤ ( ) P O , S λ = log P O , S λ ⎢ ⎥ ∑ ( ) P O λ ⎢ ⎥ S ⎣ ⎦ ( ) ( ) P O , S λ P O , S λ – Where and can be expressed as ⎡ − ⎤ ⎡ ⎤ T T ( ) 1 ( ) ∏ ∏ = π P O S λ a b o , ⎢ ⎥ ⎢ ⎥ s s s s t ⎣ + ⎦ ⎣ ⎦ t t t 1 1 = = t t 1 1 − ( ) T T 1 ( ) ∑ ∑ = π + + P O S λ a b o log , log log log s s s s t + t t t 1 1 = = t t 1 1 ( ) − T T 1 ( ) ∑ ∑ = π + + P O S λ a b o log , log log log s s s s t + t t t 1 1 64 = = t t 1 1

EM Applied to Discrete HMM Training • Rewrite the auxiliary function as w i y i ( ) ( ) ( ) ( ) = π + + Q λ λ Q λ Q λ a Q λ b , , , , π a b ( ) ( ) ? ⎡ ⎤ ⎡ ⎤ = P O , S λ P O ,s i λ N ( ) ∑ ∑ π = π = π Q λ ⎢ ⎥ ⎢ 1 ⎥ ( ) ( ) , log log π s i P O λ P O λ ⎢ ⎥ ⎢ ⎥ ⎣ 1 ⎦ ⎣ ⎦ = S i all 1 ( ) ( ) ? ⎡ ⎤ ⎡ ⎤ = = P O , S λ − − P O ,s i s j λ T N N T 1 1 , ( ) ∑ ∑ ∑ ∑ ∑ + = = t t Q λ a a 1 a ⎢ ⎥ ⎢ ⎥ ( ) ( ) , log log a s s ij P O λ P O λ ⎢ + ⎥ ⎢ ⎥ t t 1 ⎣ ⎦ ⎣ ⎦ = = = = S t i j t all 1 1 1 1 ( ) ( ) ? ⎡ ⎤ ⎡ ⎤ = P O , S λ P O ,s j λ ( ) T N ( ) ( ) ∑ ∑ ∑ ∑ ∑ = = t Q λ b b k b k ⎢ ⎥ ⎢ ⎥ ( ) ( ) , log log b s j P O λ P O λ ⎢ ⎥ ⎢ ⎥ t ⎣ ⎦ ⎣ ⎦ = = ∈ = S t j k t o v all 1 1 t k 65

EM Applied to Discrete HMM Training • The auxiliary function contains three independent ( ) π a b j k terms, , and ij i – Can be maximized individually – All of the same form ( ) ( ) N N = = = ≥ F y g y , y ,..., , y w log y , y 1 , y 0 ∑ where ∑ and 1 2 N j j j j = = j 1 j 1 w ( ) = j F y y has maximum value when : j N w ∑ j = j 1 66

EM Applied to Discrete HMM Training • Proof : Apply Lagrange Multiplier l By applying Lagrange Multiplier ( ) N N N = = + − F w log y w log y y 1 l Suppose that ∑ ∑ ∑ j j j j j = = = j 1 j 1 j 1 ∂ w w F = + = ⇒ = − ∀ Constraint j j 0 j l l ∂ y y y j j j N N N = − ⇒ = − y w w l l ∑ ∑ ∑ j j j = = = j 1 j 1 j 1 w ∴ = j y j N w ∑ j = j 1 67

EM Applied to Discrete HMM Training ( ) λ π A , B • The new model parameter set can be = , expressed as: ( ) = λ P O s i , ( ) π = = γ 1 i ( ) i λ P O 1 − − T ( ) T 1 1 ( ) ∑ ∑ = = λ ξ P O s i s j i j , , , + t t t 1 = = = = a t t 1 1 ij − − T ( ) T 1 1 ( ) ∑ ∑ = λ γ P O s i i , t t = = t t 1 1 T ( ) T ( ) ∑ ∑ = λ γ P O s i i , t t = = t t 1 1 ( ) = = o v o v = = b k s.t. s.t. t k t k i T T ( ) ( ) ∑ ∑ = λ γ P O s i i , t t = = t t 1 1 68