SSA Form & SSA-form: x 17-4 Each name is defined exactly - PDF document

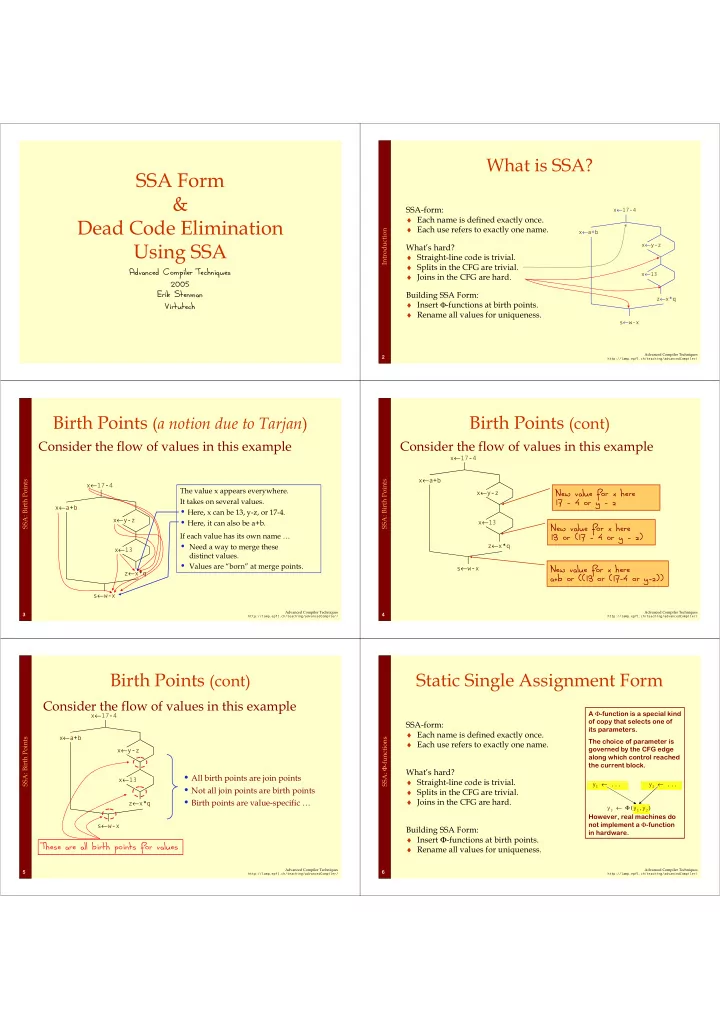
What is SSA? SSA Form & SSA-form: x ← 17-4 ♦ Each name is defined exactly once. Dead Code Elimination ♦ Each use refers to exactly one name. Introduction x ← a+b Using SSA x ← y-z What’s hard? ♦ Straight-line code is trivial. ♦ Splits in the CFG are trivial. Advanced Compiler Techniques x ← 13 ♦ Joins in the CFG are hard. 2005 Erik Stenman Building SSA Form: z ← x*q ♦ Insert Φ -functions at birth points. Virtutech ♦ Rename all values for uniqueness. s ← w-x Advanced Compiler Techniques 2 http://lamp.epfl.ch/teaching/advancedCompiler/ Birth Points ( a notion due to Tarjan ) Birth Points (cont) Consider the flow of values in this example Consider the flow of values in this example x ← 17-4 x ← a+b SSA: Birth Points SSA: Birth Points x ← 17-4 The value x appears everywhere. New value for x here x ← y-z It takes on several values. 17 - 4 or y - z x ← a+b • Here, x can be 13, y-z, or 17-4. x ← y-z • Here, it can also be a+b. x ← 13 New value for x here If each value has its own name … 13 or (17 - 4 or y - z) • Need a way to merge these z ← x*q x ← 13 distinct values. • Values are “born” at merge points. s ← w-x New value for x here z ← x*q a+b or ((13 or (17-4 or y-z)) s ← w-x Advanced Compiler Techniques Advanced Compiler Techniques 3 4 http://lamp.epfl.ch/teaching/advancedCompiler/ http://lamp.epfl.ch/teaching/advancedCompiler/ Birth Points (cont) Static Single Assignment Form Consider the flow of values in this example A Φ -function is a special kind x ← 17-4 of copy that selects one of SSA-form: its parameters. ♦ Each name is defined exactly once. x ← a+b SSA: Birth Points SSA: Φ -functions The choice of parameter is ♦ Each use refers to exactly one name. governed by the CFG edge x ← y-z along which control reached the current block. What’s hard? • All birth points are join points x ← 13 ♦ Straight-line code is trivial. y 1 ← ... y 2 ← ... • Not all join points are birth points ♦ Splits in the CFG are trivial. • Birth points are value-specific … ♦ Joins in the CFG are hard. z ← x*q y 3 ← Φ (y 1 ,y 2 ) However, real machines do not implement a Φ -function s ← w-x Building SSA Form: in hardware. ♦ Insert Φ -functions at birth points. These are all birth points for values ♦ Rename all values for uniqueness. Advanced Compiler Techniques Advanced Compiler Techniques 5 6 http://lamp.epfl.ch/teaching/advancedCompiler/ http://lamp.epfl.ch/teaching/advancedCompiler/

SSA Construction Algorithm SSA Construction Algorithm (Less high-level) (High-level sketch) 1.Insert Φ -functions. 1.Insert Φ -functions at every join for every name. SSA: Construction SSA: Construction 2.Rename values. 2.Solve reaching definitions. 3.Rename each use to the def that reaches it. ( will be unique ) … that’s all ... … of course, there is some bookkeeping to be done ... Advanced Compiler Techniques Advanced Compiler Techniques 7 8 http://lamp.epfl.ch/teaching/advancedCompiler/ http://lamp.epfl.ch/teaching/advancedCompiler/ SSA Construction Algorithm Reaching Definitions (Less high-level) The equations Domain is | DEFINITIONS DEFINITIONS |, same as SSA: Construction – Reaching Definitions number of operations R EACHES ( N 0 ) = Ø R EACHES ( N ) = ∪ P ∈ preds ( N ) D EF O UT ( P ) ∪ (R EACHES ( P ) ∩ S URVIVED ( P )) SSA: Construction – Problems 1. Insert Φ -functions at every join for every name . 2. Solve reaching definitions. 3. Rename each use to the def that reaches it. ( will be unique ) ♦ R EACHES ( N ) is the set of definitions that reach block N ♦ D EF O UT ( N ) is the set of definitions in N that reach the end of N ♦ S URVIVED ( N ) is the set of definitions not obscured by a new def in N Builds maximal SSA Computing R EACHES ( N ) What’s wrong with this approach? ♦ Use any data-flow method ( i.e., the iterative method ) ♦ Too many Φ -functions. ( precision ) ♦ Too many Φ -functions. ( space ) ♦ This particular problem has a very-fast solution ( Zadeck ) ♦ Too many Φ -functions. ( time ) ♦ Need to relate edges to Φ -functions parameters. ( bookkeeping ) F.K. Zadeck, “Incremental data-flow analysis in a structured To do better, we need a more complex approach. program editor,” Proceedings of the S IGPLAN 84 Conf. on Compiler Construction , June, 1984, pages 132-143. Advanced Compiler Techniques Advanced Compiler Techniques 9 10 http://lamp.epfl.ch/teaching/advancedCompiler/ http://lamp.epfl.ch/teaching/advancedCompiler/ SSA Construction Algorithm SSA Construction Algorithm (Less high-level) (Less high-level) SSA: Construction – Algorithm, Step 2 SSA: Construction – Algorithm, Step 1 1. Insert Φ -functions 2. Rename variables in a pre-order walk over dominator tree (use an array of stacks, one stack per global name) a.) calculate dominance frontiers Moderately complex 1 counter per Staring with the root block, B b.) find global names name for a.) generate unique names for each Φ -function subscripts for each name, build a list of blocks that define it and push them on the appropriate stacks c.) insert Φ -functions Compute list of blocks where each name b.) rewrite each operation in the block is assigned & use as a worklist i. Rewrite uses of global names with the current version ∀ global name n (from the stack) ∀ block B in which n is defined Need the end-of- This adds to ii. Rewrite definition by inventing & pushing new name ∀ block D in B ’s dominance frontier block name for the worklist ! c.) fill in Φ -function parameters of successor blocks this path { insert a Φ -function for n in D Creates the iterated d.) recurse on B ’ s children in the dominator tree dominance frontier add D to n ’s list of defining blocks e.) < on exit from block B > pop names generated in B from stacks Use a checklist to avoid putting blocks on the worklist twice; keep another checklist to avoid inserting the same Φ -function twice. Reset the state Advanced Compiler Techniques Advanced Compiler Techniques 11 12 http://lamp.epfl.ch/teaching/advancedCompiler/ http://lamp.epfl.ch/teaching/advancedCompiler/