Spiral 3-2 Signal & Image Processing Finding and exploiting - PowerPoint PPT Presentation

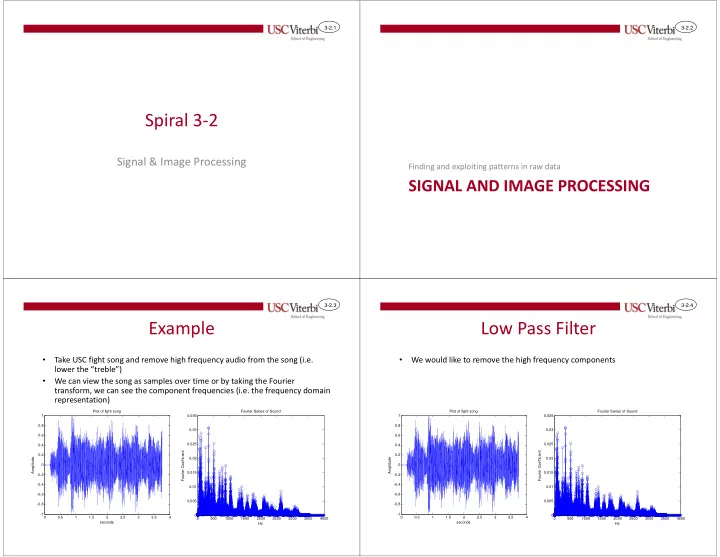
3-2.1 3-2.2 Spiral 3-2 Signal & Image Processing Finding and exploiting patterns in raw data SIGNAL AND IMAGE PROCESSING 3-2.3 3-2.4 Example Low Pass Filter • Take USC fight song and remove high frequency audio from the song (i.e. • We would like to remove the high frequency components lower the “treble”) • We can view the song as samples over time or by taking the Fourier transform, we can see the component frequencies (i.e. the frequency domain representation) Plot of fight song Fourier Series of Sound Plot of fight song Fourier Series of Sound 1 0.035 1 0.035 0.8 0.8 0.03 0.03 0.6 0.6 0.025 0.025 0.4 0.4 Fourier Coefficient Fourier Coefficient 0.2 0.2 Amplitude 0.02 Amplitude 0.02 0 0 0.015 0.015 -0.2 -0.2 -0.4 -0.4 0.01 0.01 -0.6 -0.6 0.005 0.005 -0.8 -0.8 -1 -1 0 0 0 0.5 1 1.5 2 2.5 3 3.5 4 0 0.5 1 1.5 2 2.5 3 3.5 4 0 500 1000 1500 2000 2500 3000 3500 4000 0 500 1000 1500 2000 2500 3000 3500 4000 seconds seconds Hz Hz

3-2.5 3-2.6 Tangent – Frequency Domain Fourier Decomposition • Fourier theory says any signal can be represented as • Fourier theory says we can also find the sine wave sum of different frequency sine waves components given the original signal Component Sine Waves (Freq. Domain) Individual Sine waves of 1*f, 3*f, 5*f, 7*f Sum of those sine waves Original signal Fourier Series of Composite Signal 1 1 1 1 f = 60Hz 0.8 0.8 0.8 0.9 1*f Component 0.6 0.6 0.6 0.8 0.4 0.4 0.4 3*f Component 0.7 0.2 0.2 0.2 Fourier Coefficient 0.6 5*f Component 0 0 0 0.5 -0.2 -0.2 -0.2 7*f Component 0.4 -0.4 -0.4 -0.4 0.3 9*f Component -0.6 -0.6 -0.6 0.2 -0.8 -0.8 -0.8 0.1 -1 -1 -1 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0 0 500 1000 1500 2000 2500 3000 3500 4000 Hz Fourier Composition – By summing different sine waves we Fourier Composition – By summing different sine waves we can form a square wave or any other signal can form a square wave or any other signal 3-2.7 3-2.8 Designing a Low Pass Filter Moving Average • Below is a zoomed view • By making each sample equal to the average • Removing high frequency components (parts of the signal that change of itself plus neighboring samples we tend to rapidly) means smoothing the signal or finding its basic curve and not the bumpiness smooth the signal • To do this, for each sample, make it equal to the average of neighboring pixels. 0.6 0.4 0.2 0 Original signal, Averaged Signal, -0.2 x[i] y[i] -0.4 -0.6 -0.8 0.62 0.625 0.63 0.635 0.64 0.645 0.65 0.655 0.66 0.665 0.67

3-2.9 3-2.10 Averaged Signal 8-tap Moving Average Filter • Assume each sample is the average of 8 surrounding • Averaging smoothes the waveform and samples, we can describe the output as: effectively filters out high-frequency y[i] = Σ k=0 to 7 (1/8) * x[i-k] components • Example: After averaging each sample with 8 Original signal nearest samples – y[7] = 1/8*x[7] + 1/8*x[6] + … + 1/8*x[0] 0.6 0.4 0.3 0.4 – y[8] = 1/8*x[8] + 1/8*x[7] + … + 1/8*x[1] 0.2 0.2 • If we want a weighted average rather than pure 0.1 0 0 average we can generalize from 1/8 to some weight -0.2 -0.1 coefficient: w k -0.4 -0.2 y[i] = Σ k=0 to 7 w k *x[i-k] -0.6 -0.3 -0.8 -0.4 0.62 0.625 0.63 0.635 0.64 0.645 0.65 0.655 0.66 0.665 0.67 0.62 0.625 0.63 0.635 0.64 0.645 0.65 0.655 0.66 0.665 0.67 3-2.11 3-2.12 Digital Implementation Storing Last 8 Samples • The system we want to design gets one • Since we only get one sample a clock, but need to use the last 8 samples to do our average, we need to sample per clock and produces one output save the last 8 samples sample per clock – To store values we use registers – Chain together several registers • xd1 = x[i] delayed by 1 clock • xd2 = x[i] delayed by 2 clocks Moving Average x[i] y[i] Filter clk reset

3-2.13 3-2.14 Time Space Diagram Averaging the Samples • Multiple each sample by the appropriate Clock X[i] Xd1 Xd2 Xd3 Xd4 Xd5 Xd6 Xd7 X(0) X(-1)=0 X(-2)=0 X(-3)=0 X(-4)=0 X(-5)=0 X(-6)=0 X(-7)=0 0 weight (in this case each w k = 1/8) 1 X(1) X(0) X(-1)=0 X(-2)=0 X(-3)=0 X(-4)=0 X(-5)=0 X(-6)=0 • Add up all values 2 X(2) X(1) X(0) X(-1)=0 X(-2)=0 X(-3)=0 X(-4)=0 X(-5)=0 3 X(3) X(2) X(1) X(0) X(-1)=0 X(-2)=0 X(-3)=0 X(-4)=0 4 X(4) X(3) X(2) X(1) X(0) X(-1)=0 X(-2)=0 X(-3)=0 5 X(5) X(4) X(3) X(2) X(1) X(0) X(-1)=0 X(-2)=0 6 X(6) X(5) X(4) X(3) X(2) X(1) X(0) X(-1)=0 7 X(7) X(6) X(5) X(4) X(3) X(2) X(1) X(0) 8 X(8) X(7) X(6) X(5) X(4) X(3) X(2) X(1) 9 X(9) X(8) X(7) X(6) X(5) X(4) X(3) X(2) Samples x[i] where i < 0 (negative indices) are equal to 0 since there register will be reset (cleared) at clock 0 3-2.15 3-2.16 Another Example: Image Compression • Images are just 2-D arrays (matrices) of numbers • Each number corresponds to the color or a pixel in that location • Image store those numbers in some way HW/SW Design (System on Chip) Column Index CONCEPTS

3-2.17 3-2.18 Image Compression Image Compression 129 131 130 133 132 132 130 129 128 130 131 129 129 131 130 133 132 132 130 129 128 130 131 129 130 130 131 129 131 132 131 133 130 129 129 131 130 130 131 129 131 132 131 133 130 129 129 131 132 131 130 132 132 131 130 132 134 132 131 132 134 132 131 132 133 131 133 131 156 157 156 157 153 155 153 155 154 152 154 152 207 204 207 204 208 205 208 205 1. Break Image into small blocks of pixels 129 131 130 133 129 2 1 4 129 2 1 4 129 2 0 4 130 130 131 129 2 1 2 0 2 1 2 0 2 0 2 0 132 131 130 132 3 2 1 3 3 2 1 3 2 2 0 2 134 132 131 132 5 3 2 3 5 3 2 3 4 2 2 2 2. Store the difference of each pixel and the upper left 3. We can save more space by rounding numbers to a (or some other representative pixel) smaller set of options (i.e. only even # differences) 3-2.19 3-2.20 Video Compression • Video is a sequence of still frames – 24-30 frames per second (fps) • How much difference is expected between frames? • Idea: – Store 1 of every N frames (aka key frame or I-frame), with other N-1 frames being differences from previous or next frame JPEG

3-2.21 3-2.22 JPEG Conversion Process Huffman Code • Compression algorithm 129 131 130 133 129 131 130 133 Perform 130 130 131 129 129 131 130 133 130 130 131 129 Discrete 132 131 130 132 • Variable-length code 130 130 131 129 132 131 130 132 Cosine 134 132 131 132 132 131 130 132 Transform Break into 134 132 131 132 – Each character can be coded with a different 134 132 131 132 on each 8x8 Tiles 8x8 Block number of bits 32 5 3 0 129 20 15 3 • Prefix code 32 5 3 0 Huffman 4 -1 0 1 129 20 15 3 17 -3 2 4 32 5 3 0 129 20 15 3 Coding 4 -1 0 1 3 0 0 0 17 -3 2 4 12 3 2 1 4 -1 0 1 17 -3 2 4 3 0 0 0 – No two codes start with the same prefix 2 0 0 0 12 3 2 1 10 1 -2 0 3 0 0 0 12 3 2 1 2 0 0 0 10 1 -2 0 Quantize 2 0 0 0 10 1 -2 0 • Assignment of codes to characters is based on frequency of the code in the message Storage (as .jpeg) 3-2.23 3-2.24 Huffman Example 1 Huffman Example 2 • "Mississippi" • "i boo big bruins"

3-2.25 3-2.26 Design Exercise • Design a system that breaks a 8x8 image into 4 tiles of 4x4 and: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 – Leaves the upper-left pixel of 16 17 18 19 20 21 22 23 each tile as is 32 33 34 35 36 37 38 39 – Codes the remaining 15 pixels 40 of the tile as relative values DESIGN EXERCISE based on the upper-left 56 57 58 59 60 61 62 63 – Computes the frequency of each pixel value to prepare for Huffman coding 3-2.27 3-2.28 Computing Frequencies Block Diagram • Given an array 16 numbers between 0-255 how could you compute their frequencies in software?

3-2.29 3-2.30 Addressing Verilog Description • Given the HW 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 counter that 16 17 18 19 20 21 22 23 counts 0000-1111 32 33 34 35 36 37 38 39 40 and tile counter 56 57 58 59 60 61 62 63 00-11, can you use System Address those 6-bits to 0 1 2 3 0 1 2 3 Tile 0 Tile 1 4 5 6 7 4 5 6 7 form the correct 8 9 10 11 8 9 10 11 12 13 14 15 12 13 14 15 system address? 0 1 2 3 0 1 2 3 Tile 2 Tile 3 4 5 6 7 4 5 6 7 8 9 10 11 8 9 10 11 12 13 14 15 12 13 14 15 HW Counters