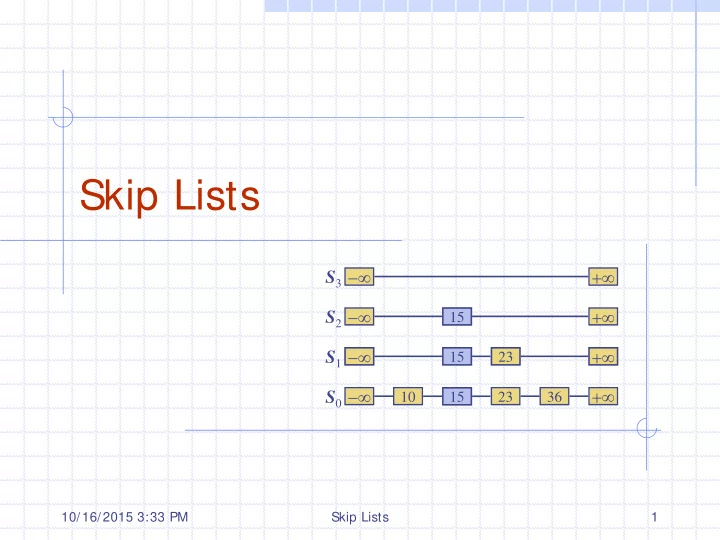
Skip Lists + S 3 + S 2 15 + S 1 15 23 + S 0 10 - PowerPoint PPT Presentation

Skip Lists −∞ +∞ S 3 −∞ +∞ S 2 15 −∞ +∞ S 1 15 23 −∞ +∞ S 0 10 15 23 36 10/16/2015 3:33 PM Skip Lists 1

Outline and Reading What is a skip list (§3.5) Operations  Search (§3.5.1)  Insertion (§3.5.2)  Deletion (§3.5.2) Implementation Analysis (§3.5.3)  Space usage  Search and update times Comparison of dictionary implementations 10/16/2015 3:33 PM Skip Lists 2

What is a Skip List A skip list for a set S of distinct (key, element) items is a series of lists S 0 , S 1 , … , S h such that Each list S i contains the special keys +∞ and −∞  List S 0 contains the keys of S in nondecreasing order  Each list is a subsequence of the previous one, i.e.,  S 0 ⊇ S 1 ⊇ … ⊇ S h List S h contains only the two special keys  We show how to use a skip list to implement the dictionary ADT S 3 −∞ +∞ S 2 −∞ +∞ 31 S 1 −∞ +∞ 23 31 34 64 −∞ +∞ S 0 12 23 26 31 34 44 56 64 78 10/16/2015 3:33 PM Skip Lists 3

Search We search for a key x in a a skip list as follows: We start at the first position of the top list  At the current position p , we compare x with y ← key ( after ( p ))  x = y : we return element ( after ( p )) x > y : we “scan forward” x < y : we “drop down” If we try to drop down past the bottom list, we return NO_SUCH_KEY  Example: search for 78 S 3 −∞ +∞ S 2 −∞ +∞ 31 S 1 −∞ +∞ 23 31 34 64 −∞ +∞ S 0 12 23 26 31 34 44 56 64 78 10/16/2015 3:33 PM Skip Lists 4

Randomized Algorithms A randomized algorithm We analyze the expected performs coin tosses (i.e., running time of a uses random bits) to control randomized algorithm under its execution the following assumptions the coins are unbiased, and It contains statements of the  type the coin tosses are  b ← random () independent if b = 0 The worst-case running time of a randomized algorithm is do A … often large but has very low else { b = 1} probability (e.g., it occurs do B … when all the coin tosses give Its running time depends on “heads”) the outcomes of the coin We use a randomized tosses algorithm to insert items into a skip list 10/16/2015 3:33 PM Skip Lists 5

Insertion To insert an item ( x , o ) into a skip list, we use a randomized algorithm: We repeatedly toss a coin until we get tails, and we denote with i  the number of times the coin came up heads If i ≥ h , we add to the skip list new lists S h + 1 , … , S i + 1 , each  containing only the two special keys We search for x in the skip list and find the positions p 0 , p 1 , …, p i  of the items with largest key less than x in each list S 0 , S 1 , … , S i For j ← 0, …, i , we insert item ( x , o ) into list S j after position p j  Example: insert key 15 , with i = 2 −∞ +∞ S 3 p 2 −∞ +∞ −∞ +∞ S 2 S 2 15 p 1 −∞ +∞ −∞ +∞ S 1 S 1 23 15 23 p 0 −∞ +∞ +∞ −∞ S 0 S 0 10 23 36 10 15 23 36 10/16/2015 3:33 PM Skip Lists 6

Deletion To remove an item with key x from a skip list, we proceed as follows: We search for x in the skip list and find the positions p 0 , p 1 , …, p i  of the items with key x , where position p j is in list S j We remove positions p 0 , p 1 , …, p i from the lists S 0 , S 1 , … , S i  We remove all but one list containing only the two special keys  Example: remove key 34 −∞ +∞ S 3 p 2 −∞ +∞ −∞ +∞ S 2 S 2 34 p 1 −∞ +∞ −∞ +∞ S 1 S 1 23 34 23 p 0 −∞ −∞ +∞ +∞ S 0 S 0 12 23 34 45 12 23 45 10/16/2015 3:33 PM Skip Lists 7

Implementation We can implement a skip list with quad-nodes A quad-node stores: item  quad-node link to the node before  link to the node after  x link to the node below  link to the node after  Also, we define special keys PLUS_INF and MINUS_INF , and we modify the key comparator to handle them 10/16/2015 3:33 PM Skip Lists 8

Space Usage Consider a skip list with n The space used by a skip list items depends on the random bits By Fact 1, we insert an item  used by each invocation of the in list S i with probability 1 / 2 i insertion algorithm By Fact 2, the expected size  We use the following two basic of list S i is n / 2 i probabilistic facts: The expected number of Fact 1: The probability of getting i nodes used by the skip list is consecutive heads when flipping a coin is 1 / 2 i = ∑ h h n 1 ∑ < n 2 n Fact 2: If each of n items is i i 2 2 = = i 0 i 0 present in a set with probability p , the expected size Thus, the expected space of the set is np usage of a skip list with n items is O ( n ) 10/16/2015 3:33 PM Skip Lists 9

Height Consider a skip list with n The running time of the items search an insertion By Fact 1, we insert an item in algorithms is affected by the  list S i with probability 1 / 2 i height h of the skip list By Fact 3, the probability that  We show that with high list S i has at least one item is at most n / 2 i probability, a skip list with n By picking i = 3log n , we have items has height O (log n ) that the probability that S 3log n We use the following has at least one item is additional probabilistic fact: at most n / 2 3log n = n / n 3 = 1 / n 2 Fact 3: If each of n events has probability p , the probability Thus a skip list with n items that at least one event has height at most 3log n with occurs is at most np probability at least 1 − 1 / n 2 10/16/2015 3:33 PM Skip Lists 10

Search and Update Times The search time in a skip list When we scan forward in a is proportional to list, the destination key does not belong to a higher list the number of drop-down  steps, plus A scan-forward step is  associated with a former coin the number of scan-forward  toss that gave tails steps By Fact 4, in each list the The drop-down steps are expected number of scan- bounded by the height of the forward steps is 2 skip list and thus are O (log n ) with high probability Thus, the expected number of scan-forward steps is O (log n ) To analyze the scan-forward steps, we use yet another We conclude that a search in a probabilistic fact: skip list takes O (log n ) expected time Fact 4: The expected number of coin tosses required in order The analysis of insertion and to get tails is 2 deletion gives similar results 10/16/2015 3:33 PM Skip Lists 11

Implementing a Dictionary Comparison of efficient dictionary implementations Search Insert Delete Notes no ordered dictionary Hash 1 1 1 methods Table expected expected expected simple to implement log n log n log n randomized insertion Skip List simple to implement high prob. high prob. high prob. (2,4) log n log n log n complex to implement Tree worst-case worst-case worst-case 10/16/2015 3:33 PM Skip Lists 12

Summary A skip list is a data Using a more complex structure for dictionaries probabilistic analysis, that uses a randomized one can show that insertion algorithm these performance In a skip list with n bounds also hold with items high probability  The expected space used Skip lists are fast and is O ( n ) simple to implement in  The expected search, insertion and deletion practice time is O (log n ) 10/16/2015 3:33 PM Skip Lists 13