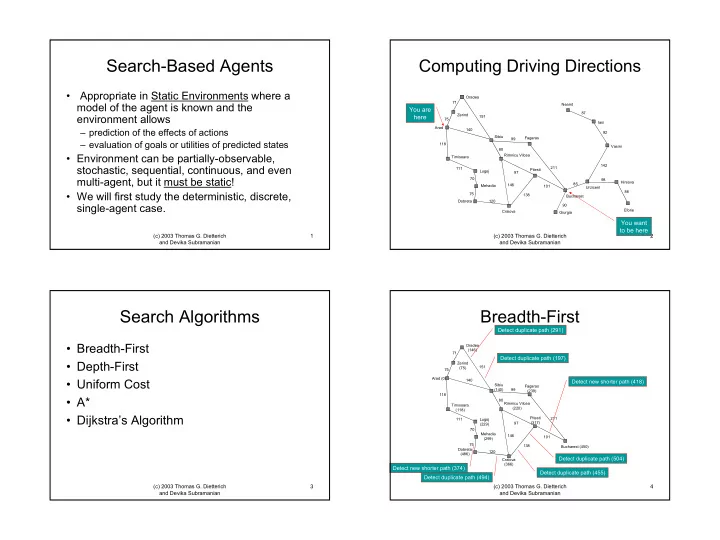
Search-Based Agents Computing Driving Directions Appropriate in - PowerPoint PPT Presentation

Search-Based Agents Computing Driving Directions • Appropriate in Static Environments where a Oradea 71 model of the agent is known and the Neamt You are 87 Zerind environment allows here 151 75 Iasi Arad – prediction of the effects of actions 140 92 Sibiu Fagaras 99 – evaluation of goals or utilities of predicted states 118 Vasini 80 • Environment can be partially-observable, Rimnicu Vilcea Timisoara 142 stochastic, sequential, continuous, and even 211 111 Pitesti Lugoj 97 multi-agent, but it must be static! 70 98 Hirsova 85 146 Mehadia 101 Urzicenl 86 • We will first study the deterministic, discrete, 75 138 Bucharest Dobreta 120 single-agent case. 90 Eforie Craiova Giurgia You want to be here (c) 2003 Thomas G. Dietterich 1 (c) 2003 Thomas G. Dietterich 2 and Devika Subramanian and Devika Subramanian Search Algorithms Breadth-First Detect duplicate path (291) • Breadth-First Oradea (146) 71 Detect duplicate path (197) • Depth-First Zerind 151 (75) 75 Arad (0) • Uniform Cost 140 Detect new shorter path (418) Sibiu Fagaras (140) 99 (239) 118 • A* 80 Rimnicu Vilcea Timisoara (220) (118) • Dijkstra’s Algorithm Pitesti 111 211 Lugoj 97 (317) (229) 70 Mehadia 146 101 (299) 75 138 Bucharest (450) Dobreta 120 (486) Detect duplicate path (504) Craiova (366) Detect new shorter path (374) Detect duplicate path (455) Detect duplicate path (494) (c) 2003 Thomas G. Dietterich 3 (c) 2003 Thomas G. Dietterich 4 and Devika Subramanian and Devika Subramanian 1

Oradea Formal Statement of Search (146) 71 Breadth-First Zerind 151 (75) 75 Problems Arad (0) 140 Sibiu Fagaras (140) 99 (239) 118 80 Rimnicu Vilcea Timisoara • State Space: set of possible “mental” states (220) (118) Pitesti 111 211 Lugoj 97 (317) (229) – cities in Romania 70 Mehadia 146 101 (299) 75 • Initial State: state from which search begins 138 Bucharest (450) Dobreta 120 (486) Craiova (366) – Arad Arad (0) • Operators: simulated actions that take the agent Zerind (75) Sibiu (140) Timisoara (118) from one mental state to another Oradea (146) Fagaras (239) Lugoj (229) Arad (150) Arad (280) Oradea (291) Rimnicu Vilcea (220) Arad (236) – traverse highway between two cities Mehadia (299) Zerind (217) Sibiu (197) Sibiu (338) Bucharest (450) Sibiu (300) Pitesti (317) Craiova (366) Timisoara (340) • Goal Test: Lugoj (369) Dobreta (374) – Is current state Bucharest? Rimnicu Vilcea (317) Bucharest (418) Craiova (455) Rimnicu Vilcea (482) Dobreta (486) Pitesti (504) Medhadia (449) Craiova (494) (c) 2003 Thomas G. Dietterich 6 and Devika Subramanian General Search Algorithm Leaf Selection Strategies • Breadth-First Search: oldest leaf (FIFO) function G ENERAL -S EARCH ( problem, strategy ) returns a solution, or failure • Depth-First Search: youngest leaf (LIFO) initialize the search tree using the initial state of problem loop do if there are no candidates for expansion then return failure • Uniform Cost Search: cheapest leaf (Priority choose a leaf node for expansion according to strategy if the node contains a goal state then return the corresponding solution Queue) else expand the node and add the resulting nodes to the search tree end • A* search: leaf with estimated shortest total path length g(x) + h(x) = f(x) � Strategy: first-in first-out queue (expand oldest leaf first) – where g(x) is length so far – and h(x) is estimate of remaining length – (Priority Queue) (c) 2003 Thomas G. Dietterich 7 (c) 2003 Thomas G. Dietterich 8 and Devika Subramanian and Devika Subramanian 2

A* Search Euclidean Distance Table • Let h(x) be a “heuristic function” that gives Arad Mehadia 366 241 an underestimate of the true distance Bucharest Neamt 0 234 between x and the goal state Craiova Oradea 160 380 – Example: Euclidean distance Dobreta Pitesti 242 100 Eforie Rimnicu Vilcea 161 193 • Let g(x) be the distance from the start to x , Fagaras Sibiu 176 253 then g(x) + h(x) is an lower bound on the Giurgiu Timisoara 77 329 length of the optimal path Hirsova Urziceni 151 80 Iasi Vaslui 226 199 Lugoj Zerind 244 374 (c) 2003 Thomas G. Dietterich 9 (c) 2003 Thomas G. Dietterich 10 and Devika Subramanian and Devika Subramanian A* Search Dijkstra’s Algorithm • Works backwards from the goal Arad (0+366=366) • Each node keeps track of the shortest Zerind (75+374=449) Sibiu (140+253=393) Timisoara (118+329=447) known path (and its length) to the goal Fagaras (239+176=415) Oradea (291+380=671) Rimnicu Vilcea (220+193=413) • Equivalent to uniform cost search starting Bucharest (450+0=450) Pitesti (317+100=417) Craiova (366+160=526) at the goal Bucharest (418+0=418) Craiova (455+160=615) • No early stopping: finds shortest path from All remaining leaves have f(x) ≥ 418, so we know they all nodes to the goal cannot have shorter paths to Bucharest (c) 2003 Thomas G. Dietterich 11 (c) 2003 Thomas G. Dietterich 12 and Devika Subramanian and Devika Subramanian 3

Local Search Algorithms Hill Climbing • Keep a single current state x � Simple hill climbing: objective function global maximum apply a randomly-chosen • Repeat operator to the current shoulder state – Apply one or more operators to x local maximum � If resulting state is better, “flat” local maximum replace current state – Evaluate the resulting states according to an Objective Function J(x) Steepest-Ascent Hill � state space – Choose one of them to replace x (or decide current Climbing: state not to replace x at all) � Apply all operators to current state, keep state • Until time limit or stopping criterion with the best value � Stop when no successors state is better (c) 2003 Thomas G. Dietterich 13 (c) 2003 Thomas G. Dietterich 14 than current state and Devika Subramanian and Devika Subramanian Gradient Ascent Gradient Descent Search • Repeat • In continuous state spaces, x = (x 1 , x 2 , …, x n ) is a vector of real values – Compute Gradient ∇ J • Continuous operator: x := x + ∆ x for any – Update x := x + η ∇ J arbitrary vector ∆ x (infinitely many operators!) • Until ∇ J ≈ 0 • Suppose J( x ) is differentiable. Then we can compute the direction of steepest increase of J by the first derivative with respect to x , the η is the “step size”, and it must be chosen • gradient: carefully • Methods such as conjugate gradient and Newton’s method choose η automatically (c) 2003 Thomas G. Dietterich 15 (c) 2003 Thomas G. Dietterich 16 and Devika Subramanian and Devika Subramanian 4

Visualizing Gradient Ascent Problems with Hill Climbing � Local optima objective function global maximum � Flat regions shoulder local maximum � Random restarts can “flat” local maximum give good results state space current state If η is too large, search may overshoot and miss the maximum or oscillate forever (c) 2003 Thomas G. Dietterich 17 (c) 2003 Thomas G. Dietterich 18 and Devika Subramanian and Devika Subramanian Simulated Annealing • T = 100 (or some large value) • Repeat – Apply randomly-chosen operator to x to obtain x ′ . – Let ∆ E = J( x ′ ) – J( x ) – If ∆ E > 0, switch to x ′ – Else switch to x ′ with probability • exp [ ∆ E/T] (large negative steps are less likely) • T := 0.99 * T (“cool” T) • Slowly decrease T (“anneal”) to zero • Stop when no changes have been accepted for many moves • Idea: Accept “down hill” steps with some probability to help escape from local minima (c) 2003 Thomas G. Dietterich 19 and Devika Subramanian 5