CS 188: Artificial Intelligence Search Continued Instructors: Anca Dragan University of California, Berkeley [These slides adapted from Dan Klein and Pieter Abbeel; ai.berkeley.edu]
Recap: Search
Search o Search problem: o States (abstraction of the world) o Actions (and costs) o Successor function (world dynamics): o {s’|s,a->s’} o Start state and goal test
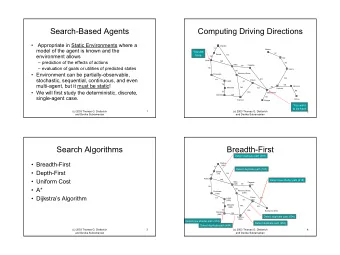
Depth-First Search
Depth-First Search G Strategy: expand a a a deepest node first c c b b e e Implementation: d d f f Fringe is a LIFO stack S h h p p r r q q S e p d q e h r b c h r p q f a a q c G p q f a q c G a
Search Algorithm Properties
Search Algorithm Properties o Complete: Guaranteed to find a solution if one exists? o Return in finite time if not? o Optimal: Guaranteed to find the least cost path? o Time complexity? 1 node b b nodes o Space complexity? … b 2 nodes m tiers o Cartoon of search tree: o b is the branching factor o m is the maximum depth b m nodes o solutions at various depths o Number of nodes in entire tree? o 1 + b + b 2 + …. b m = O(b m )
Depth-First Search (DFS) Properties o What nodes DFS expand? o Some left prefix of the tree. 1 node b o Could process the whole tree! b nodes … o If m is finite, takes time O(b m ) b 2 nodes m tiers o How much space does the fringe take? o Only has siblings on path to root, so O(bm) o Is it complete? b m nodes o m could be infinite, so only if we prevent cycles (more later) o Is it optimal? o No, it finds the “leftmost” solution, regardless of depth or cost
Breadth-First Search
Breadth-First Search G Strategy: expand a a c shallowest node first b e Implementation: Fringe d f is a FIFO queue S h p r q S e p d Search q e h r b c Tiers h r p q f a a q c p q f G a q c G a
Breadth-First Search (BFS) Properties o What nodes does BFS expand? o Processes all nodes above shallowest 1 node b solution b nodes … s tiers o Let depth of shallowest solution be s b 2 nodes o Search takes time O(b s ) b s nodes o How much space does the fringe take? b m nodes o Has roughly the last tier, so O(b s ) o Is it complete? o s must be finite if a solution exists, so yes! (if no solution, still need depth != ∞ ) o Is it optimal? o Only if costs are all 1 (more on costs later)
Video of Demo Maze Water DFS/BFS (part 1)
Video of Demo Maze Water DFS/BFS (part 2)
Iterative Deepening o Idea: get DFS’s space advantage with BFS’s time / shallow-solution b advantages … o Run a DFS with depth limit 1. If no solution… o Run a DFS with depth limit 2. If no solution… o Run a DFS with depth limit 3. ….. o Isn’t that wastefully redundant? o Generally most work happens in the lowest level searched, so not so bad!
Cost-Sensitive Search GOAL a c b e d f START h p r q
Cost-Sensitive Search GOAL a 2 2 c b 3 2 1 8 2 e d 3 f 9 8 2 START h 4 2 1 4 p r 15 q BFS finds the shortest path in terms of number of actions. How? It does not find the least-cost path. We will now cover a similar algorithm which does find the least-cost path.
Uniform Cost Search
Uniform Cost Search 2 G a Strategy: expand a c b 8 1 cheapest node first: 2 2 e 3 d f 9 2 Fringe is a priority queue 8 S h 1 (priority: cumulative cost) 1 p r q 15 0 S 9 1 e p 3 d q 16 11 5 17 e h r b 4 c 11 Cost 6 13 7 h r p q f a a contours q c 8 p q f G a q c 11 10 G a
Uniform Cost Search (UCS) Properties o What nodes does UCS expand? o Processes all nodes with cost less than cheapest solution! b c £ 1 o If that solution costs C* and arcs cost at least e , then the … “effective depth” is roughly C*/ e c £ 2 C*/ e “tiers” o Takes time O(b C*/ e ) (exponential in effective depth) c £ 3 o How much space does the fringe take? o Has roughly the last tier, so O(b C*/ e ) o Is it complete? o Assuming best solution has a finite cost and minimum arc cost is positive, yes! (if no solution, still need depth != ∞ ) o Is it optimal? o Yes! (Proof via A*)
Uniform Cost Issues o Remember: UCS explores increasing c £ 1 … cost contours c £ 2 c £ 3 o The good: UCS is complete and optimal! o The bad: o Explores options in every “direction” Start Goal o No information about goal location [Demo: empty grid UCS (L2D5)] [Demo: maze with deep/shallow o We’ll fix that soon! water DFS/BFS/UCS (L2D7)]
Video of Demo Empty UCS
Video of Demo Maze with Deep/Shallow Water --- DFS, BFS, or UCS? (part 1)
Video of Demo Maze with Deep/Shallow Water --- DFS, BFS, or UCS? (part 2)
Video of Demo Maze with Deep/Shallow Water --- DFS, BFS, or UCS? (part 3)
The One Queue o All these search algorithms are the same except for fringe strategies o Conceptually, all fringes are priority queues (i.e. collections of nodes with attached priorities) o Practically, for DFS and BFS, you can avoid the log(n) overhead from an actual priority queue, by using stacks and queues o Can even code one implementation that takes a variable queuing object
Up next: Informed Search § Informed Search o Uninformed Search § Heuristics o DFS § Greedy Search o BFS § A* Search o UCS § Graph Search
Search Heuristics § A heuristic is: § A function that estimates how close a state is to a goal § Designed for a particular search problem § Pathing? § Examples: Manhattan distance, Euclidean distance for pathing 10 5 11.2
Example: Heuristic Function h(x)
Greedy Search
Greedy Search o Expand the node that seems closest… o Is it optimal? o No. Resulting path to Bucharest is not the shortest!
Greedy Search b o Strategy: expand a node that you think is … closest to a goal state o Heuristic: estimate of distance to nearest goal for each state o A common case: b o Best-first takes you straight to the (wrong) … goal o Worst-case: like a badly-guided DFS [Demo: contours greedy empty (L3D1)] [Demo: contours greedy pacman small maze (L3D4)]
Video of Demo Contours Greedy (Empty)
Video of Demo Contours Greedy (Pacman Small Maze)
A* Search
A* Search UCS Greedy A*
Combining UCS and Greedy o Uniform-cost orders by path cost, or backward cost g(n) o Greedy orders by goal proximity, or forward cost h(n) g = 0 8 S h=6 g = 1 h=1 e a h=5 1 1 3 2 g = 9 g = 2 g = 4 S a d G b d e h=1 h=6 h=2 h=6 h=5 1 h=2 h=0 1 g = 3 g = 6 g = 10 c b c G d h=7 h=0 h=2 h=7 h=6 g = 12 G h=0 o A* Search orders by the sum: f(n) = g(n) + h(n) Example: Teg Grenager
When should A* terminate? o Should we stop when we enqueue a goal? h = 2 g h + A 2 2 S 0 3 3 S S->A 2 2 4 G h = 3 h = 0 S->B 2 1 3 2 3 B S->B->G 5 0 5 h = 1 S->A->G 4 0 4 o No: only stop when we dequeue a goal
Is A* Optimal? h = 6 1 3 A g h + S 0 7 7 S h = 7 G h = 0 S->A 1 6 7 S->G 5 0 5 5 o What went wrong? o Actual bad goal cost < estimated good goal cost o We need estimates to be less than actual costs!
Admissible Heuristics
Idea: Admissibility Inadmissible (pessimistic) heuristics Admissible (optimistic) heuristics break optimality by trapping slow down bad plans but good plans on the fringe never outweigh true costs
Admissible Heuristics o A heuristic h is admissible (optimistic) if: where is the true cost to a nearest goal o Examples: 0.0 15 11.5 o Coming up with admissible heuristics is most of what’s involved in using A* in practice.
Optimality of A* Tree Search
Optimality of A* Tree Search Assume: o A is an optimal goal node … o B is a suboptimal goal node o h is admissible Claim: o A will exit the fringe before B
Optimality of A* Tree Search: Blocking Proof: … o Imagine B is on the fringe o Some ancestor n of A is on the fringe, too (maybe A!) o Claim: n will be expanded before B 1. f(n) is less or equal to f(A) Definition of f-cost Admissibility of h h = 0 at a goal
Optimality of A* Tree Search: Blocking Proof: … o Imagine B is on the fringe o Some ancestor n of A is on the fringe, too (maybe A!) o Claim: n will be expanded before B 1. f(n) is less or equal to f(A) 2. f(A) is less than f(B) B is suboptimal h = 0 at a goal
Optimality of A* Tree Search: Blocking Proof: … o Imagine B is on the fringe o Some ancestor n of A is on the fringe, too (maybe A!) o Claim: n will be expanded before B 1. f(n) is less or equal to f(A) 2. f(A) is less than f(B) 3. n expands before B o All ancestors of A expand before B o A expands before B o A* search is optimal
Properties of A* Uniform-Cost A* b b … …
UCS vs A* Contours o Uniform-cost expands equally in all “directions” Start Goal o A* expands mainly toward the goal, but does hedge its bets to ensure optimality Start Goal [Demo: contours UCS / greedy / A* empty (L3D1)] [Demo: contours A* pacman small maze (L3D5)]
Video of Demo Contours (Empty) -- UCS
Video of Demo Contours (Empty) -- Greedy
Video of Demo Contours (Empty) – A*
Video of Demo Contours (Pacman Small Maze) – A*
Comparison Greedy Uniform Cost A*
Recommend
More recommend
