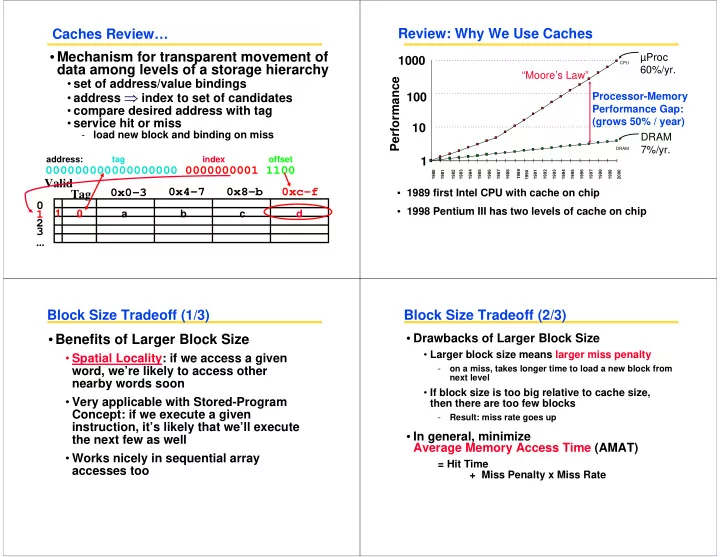
Review: Why We Use Caches Caches Review Mechanism for transparent - PowerPoint PPT Presentation

Review: Why We Use Caches Caches Review… • Mechanism for transparent movement of µProc 1000 CPU data among levels of a storage hierarchy 60%/yr. “Moore’s Law” Performance • set of address/value bindings • address ⇒ index to set of candidates 100 Processor-Memory • compare desired address with tag Performance Gap: (grows 50% / year) • service hit or miss 10 - load new block and binding on miss DRAM 7%/yr. DRAM address: tag index offset 1 000000000000000000 0000000001 1100 1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 Valid 0x4-7 0x8-b 0xc-f 0x0-3 • 1989 first Intel CPU with cache on chip Tag 0 • 1998 Pentium III has two levels of cache on chip 1 0 a b c d 1 2 3 ... Block Size Tradeoff (1/3) Block Size Tradeoff (2/3) • Benefits of Larger Block Size • Drawbacks of Larger Block Size • Larger block size means larger miss penalty • Spatial Locality: if we access a given - on a miss, takes longer time to load a new block from word, we’re likely to access other next level nearby words soon • If block size is too big relative to cache size, • Very applicable with Stored-Program then there are too few blocks Concept: if we execute a given - Result: miss rate goes up instruction, it’s likely that we’ll execute • In general, minimize the next few as well Average Memory Access Time (AMAT) • Works nicely in sequential array = Hit Time accesses too + Miss Penalty x Miss Rate

Block Size Tradeoff (3/3) Extreme Example: One Big Block Valid Bit Tag Cache Data • Hit Time = time to find and retrieve B 3 B 2 B 1 B 0 data from current level cache • Cache Size = 4 bytes Block Size = 4 bytes • Miss Penalty = average time to retrieve • Only ONE entry in the cache! data on a current level miss (includes the possibility of misses on • If item accessed, likely accessed again soon successive levels of memory • But unlikely will be accessed again immediately! hierarchy) • The next access will likely to be a miss again • Hit Rate = % of requests that are found in current level cache • Continually loading data into the cache but discard data (force out) before use it again • Miss Rate = 1 - Hit Rate • Nightmare for cache designer: Ping Pong Effect Types of Cache Misses (1/2) Block Size Tradeoff Conclusions Miss Miss Exploits Spatial Locality • “Three Cs” Model of Misses Rate Penalty • 1st C: Compulsory Misses Fewer blocks: compromises • occur when a program is first started temporal locality • cache does not contain any of that Block Size Block Size program’s data yet, so misses are bound to occur Average Increased Miss Penalty • can’t be avoided easily, so won’t focus Memory & Miss Rate on these in this course Access Time Block Size

Fully Associative Cache (1/3) Types of Cache Misses (2/2) • Memory address fields: • 2nd C: Conflict Misses • miss that occurs because two distinct memory • Tag: same as before addresses map to the same cache location • Offset: same as before • two blocks (which happen to map to the same location) can keep overwriting each other • Index: non-existant • big problem in direct-mapped caches • What does this mean? • how do we lessen the effect of these? • no “rows”: any block can go anywhere in • Dealing with Conflict Misses the cache • Solution 1: Make the cache size bigger • must compare with all tags in entire cache - Fails at some point to see if data is there • Solution 2: Multiple distinct blocks can fit in the same cache Index? Fully Associative Cache (2/3) Fully Associative Cache (3/3) • Fully Associative Cache (e.g., 32 B block) • Benefit of Fully Assoc Cache • compare tags in parallel • No Conflict Misses (since data can go anywhere) 4 31 0 Byte Offset Cache Tag (27 bits long) • Drawbacks of Fully Assoc Cache • Need hardware comparator for every Cache Data Valid Cache Tag single entry: if we have a 64KB of data in B 31 B 1 B 0 = : cache with 4B entries, we need 16K = comparators: infeasible = = : : : : =

Third Type of Cache Miss N-Way Set Associative Cache (1/4) • Capacity Misses • Memory address fields: • miss that occurs because the cache has • Tag: same as before a limited size • Offset: same as before • miss that would not occur if we increase • Index: points us to the correct “row” the size of the cache (called a set in this case) • sketchy definition, so just get the general • So what’s the difference? idea • each set contains multiple blocks • This is the primary type of miss for Fully Associative caches. • once we’ve found correct set, must compare with all tags in that set to find our data N-Way Set Associative Cache (2/4) N-Way Set Associative Cache (3/4) • Summary: • Given memory address: • cache is direct-mapped w/respect to sets • Find correct set using Index value. • each set is fully associative • Compare Tag with all Tag values in the determined set. • basically N direct-mapped caches working in parallel: each has its own • If a match occurs, hit!, otherwise a miss. valid bit and data • Finally, use the offset field as usual to find the desired data within the block.

N-Way Set Associative Cache (4/4) Associative Cache Example Cache 4 Byte Direct Memory • What’s so great about this? Index Mapped Cache Address Memory 0 • even a 2-way set assoc cache avoids a 0 1 lot of conflict misses 1 2 2 3 • hardware cost isn’t that bad: only need N 3 comparators 4 5 • In fact, for a cache with M blocks, 6 7 • it’s Direct-Mapped if it’s 1-way set assoc 8 • Recall this is how a 9 simple direct mapped • it’s Fully Assoc if it’s M-way set assoc A cache looked. B • so these two are just special cases of the C more general set associative design • This is also a 1-way set- D E associative cache! F Block Replacement Policy (1/2) Associative Cache Example Cache Memory • Direct-Mapped Cache: index completely Index Memory Address specifies which position a block can go 0 0 in on a miss 0 1 1 2 • N-Way Set Assoc: index specifies a set, 1 3 but block can occupy any position 4 within the set on a miss 5 6 7 • Fully Associative: block can be written 8 into any position • Here’s a simple 2 way set 9 associative cache. A • Question: if we have the choice, where B should we write an incoming block? C D E F

Block Replacement Policy (2/2) Block Replacement Policy: LRU • If there are any locations with valid bit • LRU (Least Recently Used) off (empty), then usually write the new • Idea: cache out block which has been block into the first one. accessed (read or write) least recently • If all possible locations already have a • Pro: temporal locality ⇒ recent past use valid block, we must pick a implies likely future use: in fact, this is a replacement policy: rule by which we very effective policy determine which block gets “cached • Con: with 2-way set assoc, easy to keep out” on a miss. track (one LRU bit); with 4-way or greater, requires complicated hardware and much time to keep track of this Block Replacement Example Block Replacement Example: LRU loc 0 loc 1 0 lru • Addresses 0, 2, 0, 1, 4, 0, ... set 0 • We have a 2-way set associative cache 0: miss, bring into set 0 (loc 0) set 1 with a four word total capacity and one word blocks. We perform the lru lru set 0 0 2 following word accesses (ignore bytes 2: miss, bring into set 0 (loc 1) set 1 for this problem): lru lru set 0 0 2 0: hit 0, 2, 0, 1, 4, 0, 2, 3, 5, 4 set 1 lru How many hits and how many misses set 0 0 2 1: miss, bring into set 1 (loc 0) will there be for the LRU block 1 lru set 1 replacement policy? lru lru 2 set 0 0 4 4: miss, bring into set 0 (loc 1, replace 2) lru set 1 1 lru lru set 0 0 4 0: hit lru set 1 1

Administrivia Big Idea • How to choose between associativity, • Do your reading! VM is coming up, block size, replacement policy? and it’s shown to be hard for students! • Any other announcements? • Design against a performance model • Minimize: Average Memory Access Time = Hit Time + Miss Penalty x Miss Rate • influenced by technology & program behavior • Note: Hit Time encompasses Hit Rate!!! • Create the illusion of a memory that is large, cheap, and fast - on average Example Ways to reduce miss rate • Assume • Larger cache • Hit Time = 1 cycle • limited by cost and technology • Miss rate = 5% • hit time of first level cache < cycle time • Miss penalty = 20 cycles • More places in the cache to put each block of memory – associativity • Calculate AMAT… • fully-associative • Avg mem access time - any block any line = 1 + 0.05 x 20 • N-way set associated = 1 + 1 cycles - N places for each block = 2 cycles - direct map: N=1