Physics 2D Lecture Slides Lecture 26: Mar 3 nd Vivek Sharma UCSD - PDF document

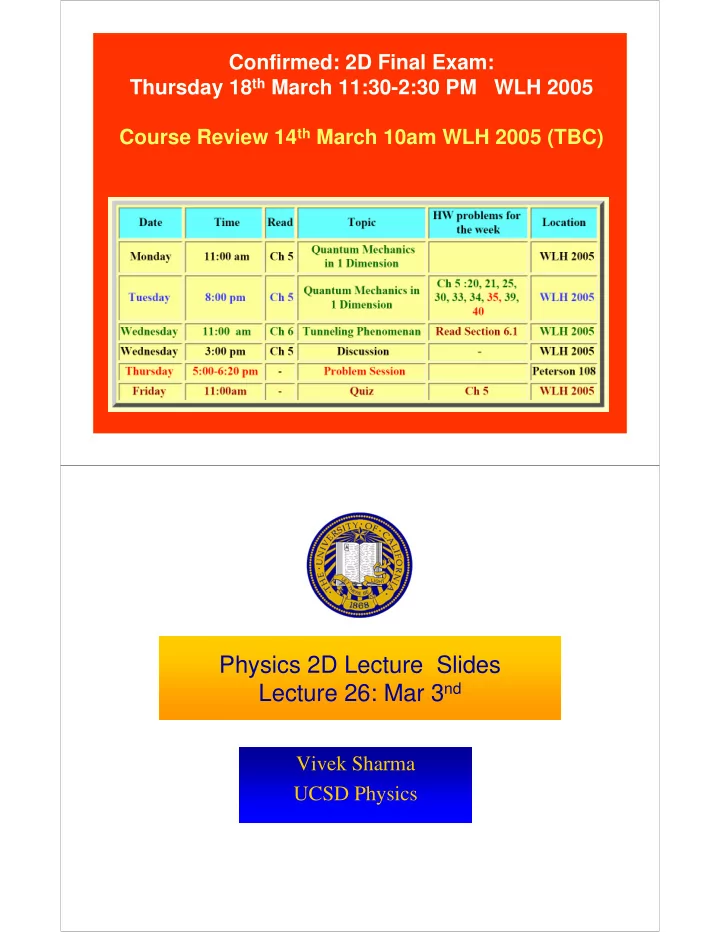
Confirmed: 2D Final Exam: Thursday 18 th March 11:30-2:30 PM WLH 2005 Course Review 14 th March 10am WLH 2005 (TBC) Physics 2D Lecture Slides Lecture 26: Mar 3 nd Vivek Sharma UCSD Physics

Measurement Expectation: Statistics Lesson • Ensemble & probable outcome of a single measurement or the average outcome of a large # of measurements ∞ n ∑ ∫ ( ) xP x dx n x + + + i i .... n x n x n x n x < >= = = = −∞ 1 1 2 2 3 3 1 i i i x ∞ + + + ... n n n n N ∫ 1 2 3 i ( ) P x dx − ∞ For a general Fn f(x) : Sharpness of A Distr ∞ n ∑ ∫ ψ ψ * ( ) ( ) ( ) x f x x dx ( ) n f x Scatter around average i i < >= = = −∞ ( ) i 1 f x ∑ ∞ − 2 N (x ) x ∫ σ ( ) i P x dx = N −∞ σ − 2 2 = ( ) ( ) x x σ → = small Sharp distr. ∆ σ Uncertainty X = Particle in the Box, n=1, find <x> & ∆ x ? π ⎛ ⎞ 2 ψ (x)= sin ⎜ x ⎟ ⎝ ⎠ L L ∞ π π ⎛ ⎞ ⎛ ⎞ 2 sin 2 ∫ <x>= ⎜ ⎟ sin ⎜ ⎟ x x x dx ⎝ ⎠ ⎝ ⎠ L L L L ∞ - π π L ⎛ ⎞ ⎛ ⎞ 2 ∫ θ 2 = sin ⎜ ⎟ , change variable = ⎜ ⎟ x x dx x ⎝ ⎠ ⎝ ⎠ L L L 0 π 2 1 ∫ ⇒ θ θ θ = − θ 2 2 <x>= sin , use sin (1 cos2 ) π 2 L 2 0 ⎡ π π ⎤ 2L ∫ ∫ ∫ ∫ ⇒ θ θ θ θ θ ⎢ ⎥ <x>= d - cos2 use ud v=uv- vdu d π 2 2 ⎣ ⎦ 0 0 ⎛ ⎞ = π 2 L L ⇒ ψ 2 <x>= ⎜ ⎟ (same result as from graphing ( )) x π 2 ⎝ 2 ⎠ 2 π L 2 2 L L ∫ = − 2 2 2 Similarly <x >= x s in ( ) x dx π 2 3 2 L 0 2 2 2 L L L ∆ > − < > = − − = 2 2 and X= <x 0.18 x L π 2 3 2 4 ∆ X= 20% of L, Particle not sharply confi ned in Box

Expectation Values & Operators: More Formally • Observable: Any particle property that can be measured – X,P, KE, E or some combination of them,e,g: x 2 – How to calculate the probable value of these quantities for a QM state ? • Operator: Associates an operator with each observable – Using these Operators, one calculates the average value of that Observable – The Operator acts on the Wavefunction (Operand) & extracts info about the Observable in a straightforward way � gets Expectation value for that observable +∞ ∫ < >= Ψ ˆ Ψ * * ( , ) [ ] ( , ) Q x t Q x t d x −∞ ˆ is the observable, [ ] is the operator Q Q < > & is the Expectation va lue Q � d Exam p les : [X] = x , [P] = i dx ∂ ∂ 2 � 2 2 [P] - = � [K] = 2 2 [E] = i ∂ ∂ m 2m x t

Operators � Information Extractors � d ˆ [p] or p = Momentum Operator i dx gives the value of average mometum in the following way: ∞ ∞ ψ + + ⎛ � ⎞ d ∫ ∫ ψ ψ ψ * * <p> = (x) [ ] ( ) p x dx = (x) ⎜ ⎟ dx ⎝ ⎠ i dx ∞ ∞ - - Similerly : Plug & play form � 2 2 d ˆ [K] or K = - gi ves the value of average K E 2 2m dx ∞ ∞ ⎛ ⎞ ψ + + � 2 2 ( ) d x ∫ ∫ ψ ψ = ψ − * * <K> = (x)[ ] ( ) (x) ⎜ ⎟ K x dx dx 2 ⎝ 2m ⎠ dx ∞ ∞ - - Similerly ∞ + ∫ ψ ψ * <U> = (x )[ U x ( )] ( ) x dx : plug in the U(x) fn for that case ∞ - ∞ ∞ ⎛ ψ ⎞ + + � 2 2 ( ) d x ∫ ∫ ψ + ψ = ψ − + * * an d <E> = (x)[ ( )] ( ) (x) ⎜ ( ) ⎟ K U x x dx U x dx 2 ⎝ ⎠ 2m dx ∞ ∞ - - Hamiltonian Operator [H] = [K] +[U] ∂ � The Energy Operator [E] = i informs you of the averag e energy ∂ t [H] & [E] Operators • [H] is a function of x • [E] is a function of t …….they are really different operators • But they produce identical results when applied to any solution of the time-dependent Schrodinger Eq. [H] Ψ (x,t) = [E] Ψ (x,t) • ⎡ ⎤ ∂ ∂ � ⎡ ⎤ 2 2 − + Ψ = Ψ � ⎢ ( , ) ⎥ ( , ) ( , ) U x t x t i x t ⎢ ⎥ ∂ ∂ 2 ⎣ ⎦ ⎣ 2 ⎦ m x t • Think of S. Eq as an expression for Energy conservation for a Quantum system

Where do Operators come from ? A touchy-feely answer :[ ] The momentum Extractor (operator) : Example p Consider as an example: Free Particle Wavefu nction π 2 h p Ψ λ = ⇒ = i(kx-wt) (x,t) = Ae ; k = , k λ � p ∂Ψ p p (x,t) p p i( x-wt) i( x-wt) Ψ = = Ψ � � (x,t) = Ae ; A e (x,t) rewrit e i i ∂ � � x ∂ ⎡ ⎤ � ⇒ Ψ Ψ (x,t) = p (x,t) ⎢ ⎥ ∂ ⎣ ⎦ i x ∂ ⎡ � ⎤ So it is not unreasonable to associate [p]= with observable p ⎢ ⎥ ∂ ⎣ ⎦ i x Example : Average Momentum of particle in box • Given the symmetry of the 1D box, we argued last time that <p> = 0 : now some inglorious math to prove it ! – Be lazy, when you can get away with a symmetry argument to solve a problem..do it & avoid the evil integration & algebra…..but be sure! π π 2 2 n n ψ = ψ = * ( ) sin( ) & ( ) sin( ) x x x x n n L L L L +∞ ∞ ⎡ � ⎤ [ ] d ∫ ∫ < >= ψ ψ = ψ ψ * * p p dx dx ⎢ ⎥ ⎣ ⎦ i dx −∞ −∞ ∞ π π π � 2 n n n ∫ < >= sin( )cos( ) p x x dx i L L L L −∞ π 1 n ∫ 2 Since sinax cosax dx = sin ...here a = ax 2a L = π x L � ⎡ ⎤ n ⇒< >= = = n π = 2 2 2 p sin ( x 0 since Sin (0) Sin ( ) 0 ⎢ ⎥ ⎣ ⎦ iL L = 0 x We knew THAT before doing any math ! Quiz 1: What is the <p> for the Quantum Oscillator in its symmetric ground state Quiz 2: What is the <p> for the Quantum Oscillator in its asymmetric first excited state

But what about the <KE> of the Particle in Box ? 2 p < >= 0 so what about expectation value of K= ? p 2m < >= < >= ≠ 0 because 0; clearly not, since we showed E=KE 0 K p Why ? What gives ? π � n = ± = ± ± Because p 2 ; " " is the key! mE n n L The AVERAGE p =0 , since particle i s moving back & forth > 2 2 p <p ≠ <KE> = < > 0 ; not ! 2m 2 m Be careful when being "lazy" Quiz: what about <KE> of a quantum Oscillator? Does similar logic apply?? Schrodinger Eqn: Stationary State Form • Recall � when potential does not depend on time explicitly U(x,t) =U(x) only…we used separation of x,t variables to simplify Ψ (x,t) = ψ (x) φ (t) & broke S. Eq. into two: one with x only and another with t only ∂ ψ � 2 2 - ( ) x + ψ = ψ ( ) ( ) ( ) U x x E x ∂ 2 2m x Ψ = ψ φ ( , ) ( ) ( ) x t x t ∂ φ ( ) t = φ � ( ) i E t ∂ t How to put Humpty-Dumpty back together ? e.g to say how to go from an expression of ψ (x) →Ψ (x,t) which describes time-evolution of the overall wave function

Schrodinger Eqn: Stationary State Form d 1 d ( ) f t [ ] = Since ln ( ) f t dt ( ) dt f t ∂ φ ∂ φ ( ) 1 ( ) t t E iE = φ = = − � In i ( ) , rewrite as E t ∂ φ ∂ � � t ( ) t t i integrate both sides w.r.t. time and = ∂ φ φ t t t t 1 ( ) 1 d ( ) t iE t iE ∫ ∫ ∫ = − ⇒ = − dt dt dt φ ∂ φ � � ( ) t ( ) dt t t t=0 0 0 iE ∴ φ − φ = − ln ( ) ln (0) , now exponentiate both sides t t � iEt − ⇒ φ = φ φ = � ( ) (0) ; (0) constant= initial condition = 1 (e.g) t e iE iE − − t t ⇒ φ = Ψ ψ � � ( ) & Thus (x,t)= (x) where E = energy of system t e e Schrodinger Eqn: Stationary State Form iE iE iE iE + − − t t t t = Ψ Ψ = ψ ψ = ψ ψ = ψ * * * 2 � � � � ( , ) ( ) ( ) ( ) ( ) | ( ) | P x t x e x e x x e x In such cases, P(x,t) is INDEPENDENT of time. These are called "stationary" states because Prob is independent of tim e Examples : Pa rtic le in a box (why?) : Quantum Os cill ator (why?) Total energy of the system depends on the spatial o rientation of the system : charteristic of the pote ntia l U(x,t) !

The Case of a Rusty “Twisted Pair” of Naked Wires & How Quantum Mechanics Saved ECE Majors ! Oxide layer Wire #1 Wire #2 • Twisted pair of Cu Wire (metal) in virgin form • Does not stay that way for long in the atmosphere •Gets oxidized in dry air quickly Cu � Cu 2 O •In wet air Cu � Cu(OH) 2 (the green stuff on wires) • Oxides or Hydride are non-conducting ..so no current can flow across the junction between two metal wires No current means no circuits � no EE, no ECE !! • • All ECE majors must now switch to Chemistry instead & play with benzene !!! Bad news ! Potential Barrier U E<U Transmitted ? x Description of Potential U = 0 x < 0 (Region I ) U = U 0 < x < L (Region II) U = 0 x > L (Region III) Consider George as a “free Particle/Wave” with Energy E incident from Left Free particle are under no Force; have wavefunctions like Ψ = A e i(kx-wt) or B e i(-kx-wt)