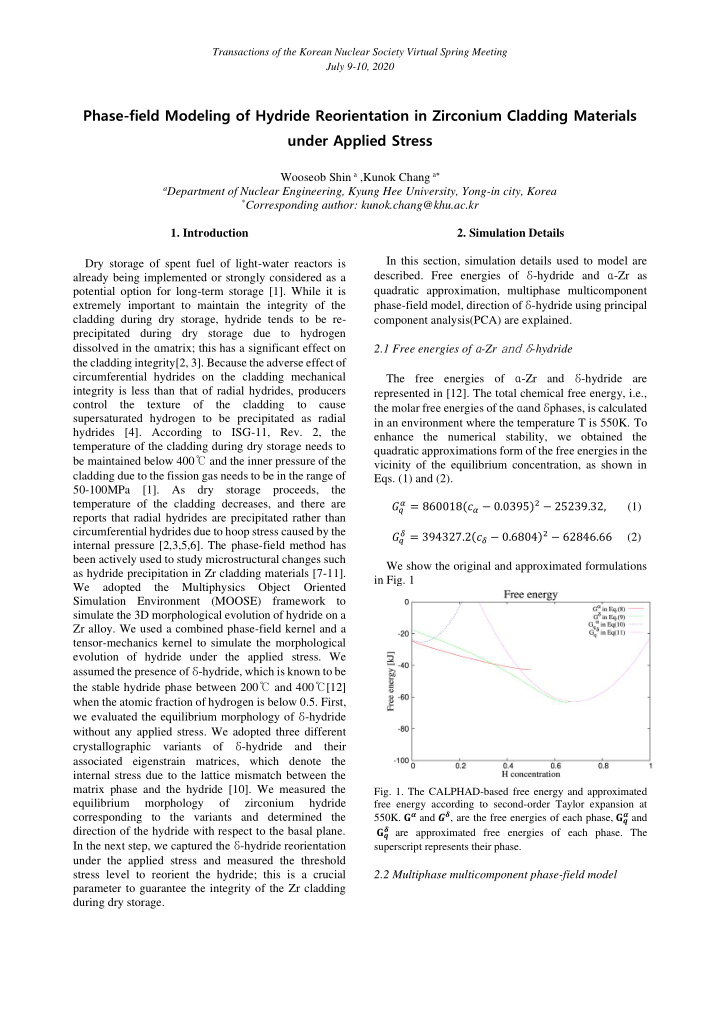



Transactions of the Korean Nuclear Society Virtual Spring Meeting July 9-10, 2020 Phase-field Modeling of Hydride Reorientation in Zirconium Cladding Materials under Applied Stress Wooseob Shin a ,Kunok Chang a a Department of Nuclear Engineering, Kyung Hee University, Yong-in city, Korea * Corresponding author: kunok.chang@khu.ac.kr 1. Introduction 2. Simulation Details In this section, simulation details used to model are Dry storage of spent fuel of light-water reactors is described. Free energies of δ -hydride and α -Zr as already being implemented or strongly considered as a quadratic approximation, multiphase multicomponent potential option for long-term storage [1]. While it is phase-field model, direction of δ -hydride using principal extremely important to maintain the integrity of the cladding during dry storage, hydride tends to be re- component analysis(PCA) are explained. precipitated during dry storage due to hydrogen dissolved in the α matrix; this has a significant effect on 2.1 Free energies of α -Zr and δ -hydride the cladding integrity[2, 3]. Because the adverse effect of circumferential hydrides on the cladding mechanical The free energies of α -Zr and δ -hydride are integrity is less than that of radial hydrides, producers represented in [12]. The total chemical free energy, i.e., control the texture of the cladding to cause the molar free energies of the α and δ phases, is calculated supersaturated hydrogen to be precipitated as radial in an environment where the temperature T is 550K. To hydrides [4]. According to ISG-11, Rev. 2, the enhance the numerical stability, we obtained the temperature of the cladding during dry storage needs to quadratic approximations form of the free energies in the be maintained below 400 ℃ and the inner pressure of the vicinity of the equilibrium concentration, as shown in cladding due to the fission gas needs to be in the range of Eqs. (1) and (2). 50-100MPa [1]. As dry storage proceeds, the 𝛽 = 860018(𝑑 𝛽 − 0.0395) 2 − 25239.32, (1) temperature of the cladding decreases, and there are 𝐻 𝑟 reports that radial hydrides are precipitated rather than circumferential hydrides due to hoop stress caused by the 𝜀 = 394327.2(𝑑 𝜀 − 0.6804) 2 − 62846.66 (2) 𝐻 𝑟 internal pressure [2,3,5,6]. The phase-field method has been actively used to study microstructural changes such We show the original and approximated formulations as hydride precipitation in Zr cladding materials [7-11]. in Fig. 1 We adopted the Multiphysics Object Oriented Simulation Environment (MOOSE) framework to simulate the 3D morphological evolution of hydride on a Zr alloy. We used a combined phase-field kernel and a tensor-mechanics kernel to simulate the morphological evolution of hydride under the applied stress. We assumed the presence of δ -hydride, which is known to be the stable hydride phase between 200 ℃ and 400 ℃ [12] when the atomic fraction of hydrogen is below 0.5. First, we evaluated the equilibrium morphology of δ -hydride without any applied stress. We adopted three different crystallographic variants of δ -hydride and their associated eigenstrain matrices, which denote the internal stress due to the lattice mismatch between the matrix phase and the hydride [10]. We measured the Fig. 1. The CALPHAD-based free energy and approximated equilibrium morphology of zirconium hydride free energy according to second-order Taylor expansion at 550K. 𝐇 𝜷 and 𝑯 𝜺 , are the free energies of each phase, 𝐇 𝒓 𝜷 and corresponding to the variants and determined the 𝜺 are approximated free energies of each phase. The direction of the hydride with respect to the basal plane. 𝐇 𝒓 In the next step, we captured the δ -hydride reorientation superscript represents their phase. under the applied stress and measured the threshold stress level to reorient the hydride; this is a crucial 2.2 Multiphase multicomponent phase-field model parameter to guarantee the integrity of the Zr cladding during dry storage.
Transactions of the Korean Nuclear Society Virtual Spring Meeting July 9-10, 2020 𝜀 ] = 0 (11) 𝛽 + h(η)σ kl Cahn-Hilliard equation [13] with respect to the ∇ ⋅ σ ij = ∇ ⋅ [ (1 − h(η))σ ij concentration of hydrogen and the Allen-Cahn equation 𝛽 = C ijkl 𝛽 ϵ ij [14] with respect to the structural parameter η as follow: 𝛽 is the total stress implemented 𝑓𝑚 , σ 𝑗𝑘 where σ 𝑗𝑘 𝜀 𝜗 𝑗𝑘 𝜀 = C ijkl 𝑓𝑚 , σ 𝑗𝑘 𝜀 is the total on the α -Zr matrix and σ 𝑗𝑘 ∂c(r, t) = ∇ ⋅ [M∇ (∂g 𝑑ℎ𝑓𝑛 )] , (3) stress implemented on the δ -hydride. 𝜖𝑢 𝜖𝑑 To investigate the effect of the applied stress in the ∂η 𝜖𝑢 = −L (∂g 𝑑ℎ𝑓𝑛 2 ∇ 2 η + ∂E 𝑓𝑚𝑏𝑡 morphological and directional transition of δ -hydride, − κ 𝜃 𝜖𝜃 ), (4) 𝜖𝜃 the applied stress σ app was implemented via a displacement boundary condition. where M is the hydrogen mobility; L is the kinetic coefficient of η ; g 𝑑ℎ𝑓𝑛 is the bulk free energy density; 2.4 Measurement of direction of the hydride E 𝑓𝑚𝑏𝑡 is the elastic strain energy; κ 𝜃 is the gradient energy coefficient associated with an interface energy. To determine the direction of the δ -hydride and its angle The constraint equations for the concentrations are the to the z-axis after reorientation, we performed a principal mass conservation equation and the pointwise equality component analysis(PCA) [17]. Voxels with hydrogen equation of the chemical potentials of the phases. The concentrations greater than 0.1 were assumed to be KKS model implemented in this study is a two-phase belong to δ -hydride. Then, we calculated the mean model with concentration variables c 𝛽 and c 𝜀 , in values of the x-, y-, and z-coordinates, and we addition to the global concentration c following Eq.(5). constructed the covariance matrix (A), which is obtained c 𝛽 and c 𝜀 are the molar fractions of atomic H in the by calculating the differences in the coordinates between matrix and δ -hydride,respectively. each position and the mean values. We obtained the eigenvalue λ and its associated eigenvector: c(r, t) = (1 − ℎ(𝜃))𝑑 𝛽 + ℎ(𝜃)𝑑 𝜀 (5) Au = λu (12) The free energies of α and δ are functions of the solute (A − λI)𝑣 = 0 (13) concentrations of each phase. The pointwise equality of the diffusion potentials of each phase is shown in Eq. (6). Where A is a covariance matrix of the data, λ is a ∂G 𝛽 𝜖𝐻 𝜀 scalar called the eigenvalue associated with the 𝜖𝑑 𝛽 = 𝜖𝑑 𝜀 (6) eigenvector and u is the eigenvector of the covariance matrix A maximizing the variance in the voxels of δ - 2.3 Elastic strain energy hydride. We assume that the hydride direction u, which is the eigenvector, corresponds to the maximum value of The elastic strain energy was computed using the the eigenvalue. Voigh-Taylor scheme [15]. When δ -hydride precipitates in α -Zr, the elastic strain energy is derived from the structural difference between δ -hydride and α -Zr. δ - hydride is an interstitial solid solution having a fcc structure and α -Zr is an interstitial solid solution having an hcp structure. The elastic strain energy E 𝑓𝑚𝑏𝑡 can be calculated as shown in Eqs. (7) - (10) [16]. 𝛽 𝜀 E 𝑓𝑚𝑏𝑡 = (1 − ℎ(𝜃))𝐹 𝑓𝑚𝑏𝑡 + h(η)𝐹 𝑓𝑚𝑏𝑡 (7) 1 𝛽 ϵ 𝑗𝑘 𝑓𝑚,𝛽 = 1 𝛽 𝜗 𝑗𝑘 𝜗 𝑙𝑚 (8) 𝑓𝑚,𝛽 ϵ 𝑙𝑚 𝛽 E 𝑓𝑚𝑏𝑡 = 2 𝐷 𝑗𝑘𝑙𝑚 2 𝐷 𝑗𝑘𝑙𝑚 𝑓𝑚,𝜀 = 1 1 𝛽 (𝜗 𝑗𝑘 − 𝜗 𝑗𝑘 𝑓𝑚,𝜀 ϵ 𝑙𝑚 𝜀 𝜀 00 )(𝜗 𝑙𝑚 − 𝜗 𝑙𝑚 00 ) (9) E 𝑓𝑚𝑏𝑡 = 2 𝐷 𝑗𝑘𝑙𝑚 ϵ 𝑗𝑘 2 𝐷 𝑗𝑘𝑙𝑚 𝜖𝑣 𝑗 (𝑠) 𝜖𝑣 𝑘 (𝑠) 1 ϵ ij = 2 [ 𝜖𝑦 𝑗 + 𝜖𝑦 𝑘 ] (10) Fig. 2. The principal component u of 𝛆 -hydride after 𝛽 is the elastic modulus tensor of the α -Zr Here, C ijkl reorientation and the angle between z-axis and u 𝜀 matrix, C 𝑗𝑘𝑙𝑚 is the elastic modulus tensor of δ -hydride; 3. Results el is the elastic tensor; ϵ ij is the eigenstrain tensor[16]. ϵ 𝑗𝑘 To solve the mechanical equilibrium equation in Eq. We placed a spherical hydride at the center of the (11), the stress was interpolated as a function of the simulation cell and found that the equilibrium structural parameter η , assuming the quasi-steady morphology of the hydride was platelet shaped for three approximation [15] with
Recommend
More recommend