Phase dynamics 2 1 Spike trains, firing rates, and synchrony 1. - PDF document

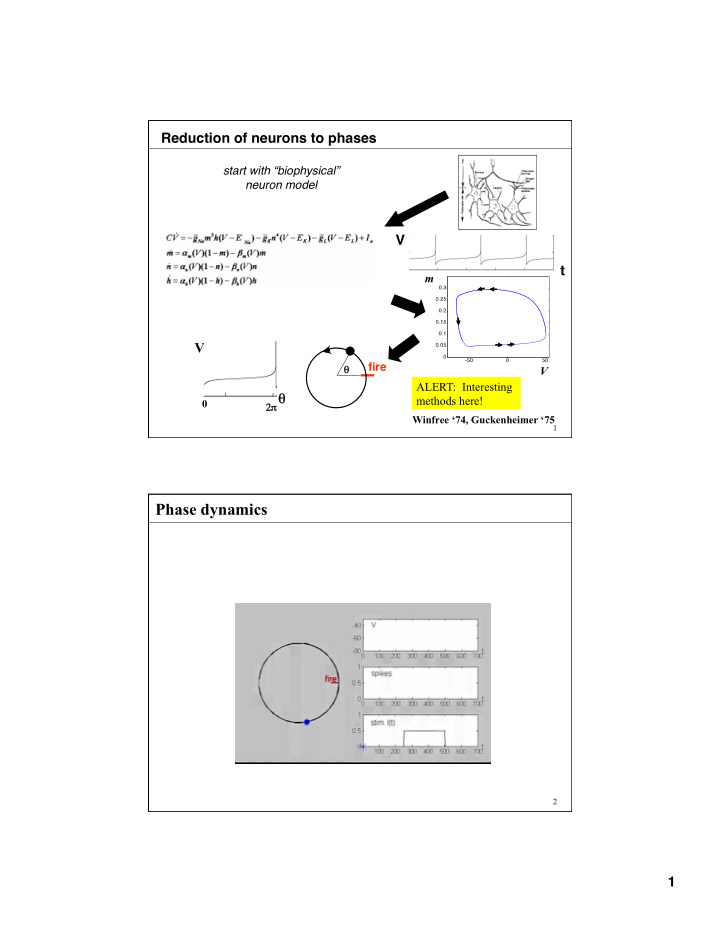
Reduction of neurons to phases start with “biophysical” neuron model V t m V fire θ V ALERT: Interesting θ methods here! 0 2 π π Winfree ‘74, Guckenheimer ‘75 1 Phase dynamics 2 1

Spike trains, firing rates, and synchrony 1. Decorrelated firing 2. Synchronized firing 3. Anti-synchronized, frequency-doubled firing 3 Roles for synchrony – 1) Synchrony allows information to propagate through “layers” of neurons – 2) Synchrony enables new information processing strategies 4 2

A role for synchrony in signal transmission Can the population trigger upstream cells? Answer depends on synchrony … “synchrony controls salience of representation” neurons 1,….N v j (t) 5 If average input <I> from upstream neurons insufficient to cause firing, need FLUCTUATIONS in I due to synchrony to drive V above spiking threshold (“detecting” upstream event) V(t) 1 I ~ pop. f. rate I ~ const 0 V(t) 1 I fluctuates <I> same 0 Shelley, Cai, Rangan, Tao, McLaughlin, Shapley – 6 Fluctuation driven firing (related) 3

Another role for synchrony … • Hypothesis – alpha, beta, gamma rhythms set up “substrate” on which further neural computations are based. • gamma (30-80 Hz) … cognition ; synchrony at this frequency when “binding” together features of object, or in attention • beta (12-30 Hz) … intense mental activity • alpha (8-12 Hz) … wakefulness, reward? • delta (1-4 Hz) … sleep 7 E.g. … • Measurements of synchrony in visual cortex during binocular rivalry DOMINANT task indicate greater EYE synchrony among “currently” dominant neurons NON- DOMINANT EYE from Fries et al 1997 8 4

Three mechanisms for the generation of synchrony 1) Recurrent connections in a network 2) Feed-forward connections among layers Diesmann, Gewaltig, Aertsen Nature 402, 529, 1999. 3) Shared, fluctuating inputs to a population I(t) Entrainment -- no connections! 9 Three mechanisms for the generation of synchrony 1) Recurrent connections in a network 2) Feed-forward connections among layers Diesmann, Gewaltig, Aertsen Nature 402, 529, 1999. 3) Shared, fluctuating inputs to a population I(t) Entrainment -- no connections! 10 5

recall …. reduction of neurons to phases start with biophysically plausible neuron model V t m V fire θ V ALERT: Interesting θ methods here! 0 2 π π Winfree ‘74, Guckenheimer ‘75 11 Reduction of neurons to phases [Coddington and Levinson, 1955, Winfree, 1974, Guckenheimer, 1985] In nbhd. of limit cycle, define variable θ ( V,m,n,h ) such that: Strategy: start on limit cycle itself, where say V( θ ) =V( ω t). nbhd. Then define level sets of θ with same “asymptotic phase” on limit cycle m 12 6

Recall how neurons communicate… chemical synapse post- action synaptic potential in potential in neuron 1 neuron 2 causes… 13 Kandel and Schwartz (Chemical) Synapse +I syn (t) g syn (t)*(V syn -V) Excitatory synapse: V syn > V rest Inhibitory synapse: V syn < V rest 14 7

Approximating the synaptic current dV dt = ... +I syn (t) g syn (t)*(V syn -V) assuming conductance impulse is brief, set I syn (t)=h* δ (t) , h>0 Excitatory synapse: V syn > V rest Inhibitory synapse: V syn < V rest , h<0 V → V + h Δ V 15 For phase dynamics … natural frequency phase response curve (phase sensitivity curve) fire θ π π =0 θ =0 16 8

Finding z( θ ) . Asymptotic phase property of field θ ( V,q ) gives nice way to calculate standard way to calculate partial limit cycle deriv. -- must Δ V know θ ( V,q ) in Δ θ nbhd. of lim cycle. level sets of θ ( V,q ) BUT! Easier to Glass and Mackey, wait and Winfree, Ermentrout and Kopell, Izhikevich, measure Δ θ as Δ θ Park and Kim, and difference in others asym. phase 17 Finding z( θ ) . Calculating the phase response curve: , parameterized by θ Jeff Moehlis perturb with 5 mV stim. 18 9

Have phase dynamics … that you could directly derive from the laboratory ! Glass and Mackey, Winfree natural frequency phase response curve (phase sensitivity curve) θ fire π π θ =0 =0 19 Phase response curves for different neurons look very different! [Ermentrout and Kopell, Van-Vreeswick, Bressloff, Izhekevich, Moehlis, Holmes, S-B] Leaky Hodgkin-Huxley Integrate and Fire 20 10

SNIPER (Ermentrout, 1996) Hopf (Erm. + Kopell, 1984) Degenerate Hopf / Bautin Homoclinic 21 Phase response curves for different neurons look very different! [Ermentrout and Kopell, Van-Vreeswick, Bressloff, Izhekevich, Moehlis, Holmes, S-B] Leaky Hodgkin-Huxley Integrate and Fire 22 11

Study synchrony in “network” of two coupled neurons I syn (t) 23 OK … let’s take the simplest imaginable case … 24 12

OK … let’s take the simplest imaginable case … 25 OK … let’s take the simplest imaginable case for z -- IF PRC z( θ ) h>0 excit. synapse 26 13

OK … let’s take the simplest imaginable case for z -- IF PRC z( θ ) Moral: coupling two neurons together does nothing if this coupling is not voltage (phase) dependent 27 Next, consider the leaky integrate and fire model 28 14

The Leaky integrate and fire model 29 The Leaky integrate and fire model PRC z( θ ) 30 15

PRC z( θ ) Moral: “Fast” excitatory coupling can synchronize LIF neurons … 31 Next, back to Hodgkin-Huxley! 32 16

The Hodgkin-Huxley model PRC z( θ ) 33 The Hodgkin-Huxley model PRC z( θ ) Moral: (again) “Fast” excitatory coupling can synchronize HH neurons … 34 17

Analyze via Poincare map between firing times of θ 1 Nancy Kopell, Bard Ermentrout, -- “weak coupling theory” Fire, θ =0 θ 1 ( n) θ 2 (n) θ 1 fire θ 2 θ 1 ( n+1) θ 2 (n+1) 35 Phase-difference map See: synchronized state θ 12 =0 is stable fixed point for map 36 18

Let’s try (as our last example) Very common in neural models … 37 The “Hodgkin Huxley plus A current” model Outward currents Inward currents I Na I K 38 19

The “Hodgkin Huxley plus A current” model 39 The “Hodgkin Huxley plus A current” model PRC z( θ ) Moral: Excitatory coupling actually DEsynchronizes HH neurons with A currents Stable “anti-synchronized” state However, inhibition does synchronize … “When inhibtion, not excitation, synchronizes…” Van Vreeswijk et al 1995 40 20

In fact, there are other types of stable antisynchronous states • N neurons, (slow) inhibitory synapses, Hodgkin-Huxley model: Multiple stable states N=24 Each corresponds to a different 
 effective frequency for the N neurons Used by Rinzel to explain co- existence of delta (1-4 Hz) and “spindling” (8-14) Hz. rhythms [deep vs light sleep] – thalamo – cortical cells 41 Beyond impulse coupling Brain has gap junctions, Kuramoto, Kopell, Ermentrout -- average coupling functions: as well as slow chemical get a system depending on phase synapses. differences only 42 21

Symmetry arguments: exists huge variety of rotating equilibria [Ashwin, Swift, Okuda, S-B.] Proposition. f odd, satisfy inequality Kuramoto, Kopell, Ermentrout --  solutions of form average coupling functions: get a system depending on phase differences only Also, in general get: k 1 2 π /m δ 1 k 2 43 Contrasts situation for sin coupling Proposition. For f(.) = sin(.) in-phase state N N is globally stable [Use gradient dynamics] [Strogatz, S-B, Kuramoto,Okuda] 44 22

Synchronized firing requires similar frequencies ω i = 3 +- 0.5 Hz ω i = 3 +- 1.0 Hz ω i = 3 +- 1.5 Hz 45 • this fact (!) allowed J. Hopfield and C. Brody to develop a new theory of speech recognition 1. (features of) incoming word trigger “o – n – e ” neural firing in a family of neurons, each of which has a different frequency decay ω i rate 2. couple together -- with appropriate synapses - neurons that have overlapping frequencies when target word spoken time (sec) PNAS (2001) vol. 98, 1282–1287 46 23

• “only” get overlap (among frequencies of selected neurons) when target word is presented “o n e ” e.g. “n e o ” PNAS (2001) vol. 98, 1282–1287 47 1. (features of) incoming word trigger “o – n – e ” neural firing in a family of neurons, each of which has a different frequency decay rate 2. couple together -- with appropriate coupling- - neurons that have overlapping frequencies when target word spoken Spike(s) 3. Once the selected neurons synchronize, they drive “detector” cell above its threshold PNAS (2001) vol. 98, 1282–1287 48 24

SUMMARY – 1) Synchrony allows information to propagate through “layers” of neurons • Synchronized activity can be necessary to trigger “downstream” cells – 2) Coupling and rhythms yield new computational strategies • Diverse neurons give diverse results – frequency-doubling and antiphase states – significance for computation and beautiful mathematics (N. Kopell) • Speech recognition (Hopfield and Brody) and may other applications! 49 Three mechanisms for the generation of synchrony 1) Recurrent connections in a network 2) Feed-forward connections among layers Diesmann, Gewaltig, Aertsen Nature 402, 529, 1999. 3) Shared, fluctuating inputs to a population I(t) Entrainment -- no connections! 50 25