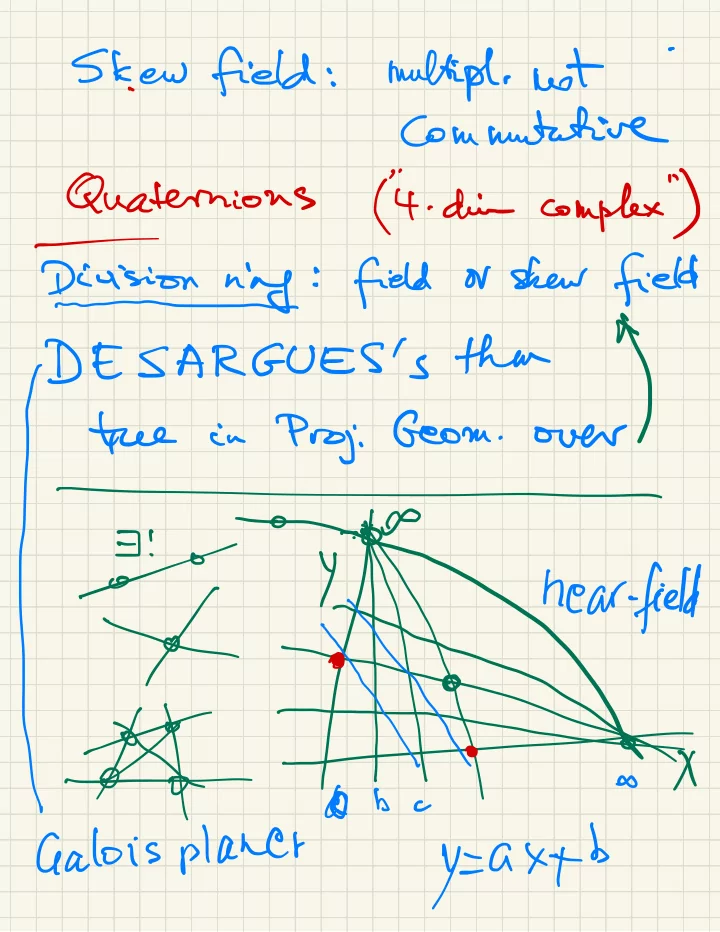

Skew field : multiple . not . Commutative ' ' " ) Quaternions 4. din complex ( or skew field : field over ) ^ DESARGUES 's than |P in Prog : Geom Hue . - ¥¥÷÷* ⇒ * Y near-field . do b c y=ax+b Ga
's plane prog DESARGUES ← division ring ( are fields Finite division rig EDDERBURN 2 → Galois finite - F finite non - DES . planes = # pts on order htt h : a line 117=111 n' tntl - - f W={ n ftp.p . of order n } N z { prime powers )
✓ = { orders of finite pp . } N Z { prime powers } known f. pp all . s have prime power order - - RYSER TAM BRUCK n =L mod 4 Tf or 2 • N E N ' ) , b) ( n = a 't b ⇒ ( Fa - 3 45 6 7 89 10 11 12 2 u r - f r - ✓ X u - p C. W . H . LAM 175 10 EIN 2 1990 •
SQUARE LATIN hxn 2-332 11 2231 13 12.21 33 I. Squares ORTHOGONAL n odd 23 . If EI ⇒ 7- pair of ortho g. L . Squares 4 × 4 F EX . i . . . bxb F EI " axa . → ab x ab EULER 2141 missing h : " 36 officers problem " h=6
⇒ 6 × 6 No 1903 • TERRY : HE 2 (4) 1960 's BOSE - SHRIKHANDE - PARKER Hn E 2 (4) n > G F pair of ortho L Sgs , only exception n = 6 - n - pk ⇒ Fn - I If EI . pairwise orth Lsgs - Sf EI L . ( m are . , L . Sgs rainworth nxn . - l m En Et - ← Ffpp ardern . - Fn - I
LATIN RECTANGLE kxn 11237 rows : perm 's of 2312 I ? Col 's : all el 's distinct Every Latin rectangle THI . Sq completed to a L can .
SDR SYSTEMS of REPRESENTATIVES DISTINCT H=( V. E ) . Em } E={ E , . . . EE , all vi. distinct ve - • A EE if SDR No ← m > n ÷÷ . ease I !f¥il4I ! - obstacle Hall 3- SDR ⇒ * Hale .gs#oSDRG6oDCHARACT - HILL TAM KENG
DENYING 1916 kzl k - uniform , k - regular hyp . Hall condita . → satisfies EI ( § obstacle ) ftp.iI-SDRE#kxnL.Recfayle Ken → extend to L . Rect . date ) x n - incidence matrix m=n4 M /¥¥/ bk4k= Et ? i k . k¥0 ⑨ ÷ ④ . .tn : Fwm =L k n , Ej E Em Col on 17=1 = # rook placements # SDRS
A = Cag . ) nxn Permanent per CAKE IT a i sci ) GE pen - = per M # SD Rs I incid . matrix - A : stochastic matrix : * row : prob . distribution aij to ¥ W =/ , ai ; A doubly stochastic : & same for columns ( i ! ! ) Iho . motor . . ? ) perm ' .
A doubly Stoch : aij 20 A Sow a l Solemn =L tf EXAMPLES permutation matrices ! ! : it n ! a- = - Per ( pen . matrix ) = 1 Der ( I J ) > In h ' = hi Per ( T ) = h ! Per A- § Tain !
( ( a ) - ha 2 THM Per CI ) =L Perl 's 5) =n÷ - are " permanent confect Vander Woerden 's . µ ±÷E¥%±r " h PERMANENT IN EQ . EGTRYCHEVTIALIKMAN 1976 ER E t per A =L ⇐ A permit . matrix K - unit → MANY , k - reg SDR Lat . Sg Llnl → MANY -7 STS "
Recommend
More recommend