= = p CSE 541 x x x x = n p 1-norm: x x = - PowerPoint PPT Presentation

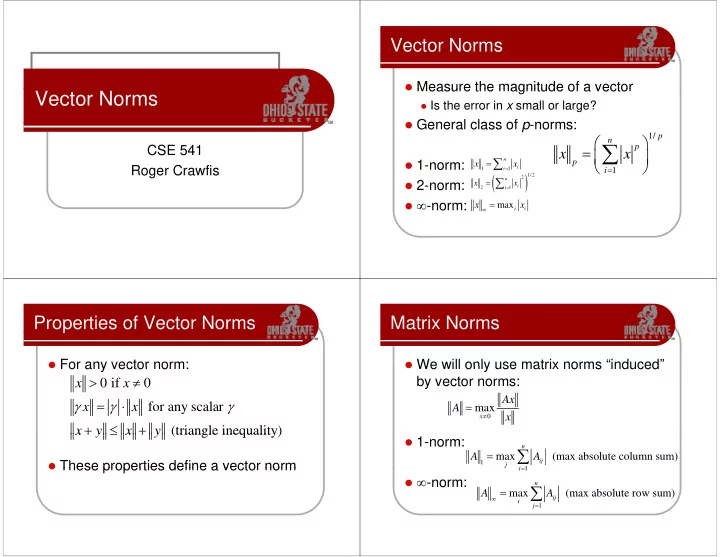
Vector Norms � Measure the magnitude of a vector � Measure the magnitude of a vector Vector Norms � Is the error in x small or large? � General class of p -norms: � General class of p norms: 1/ p ⎛ ⎞ n ∑ ∑ = ⎜ = ⎜ p CSE 541 x x x x ⎟ ⎟ = ∑ n ⎝ ⎠ p � 1-norm: x x = Roger Crawfis = i 1 i 1 i 1 ( ( ) ) = ∑ 1/2 2 n � 2-norm: o x x = i 2 i 1 � ∞ -norm: ∞ = x max i x i Properties of Vector Norms p Matrix Norms � For any vector norm: � For any vector norm: � We will only use matrix norms induced � We will only use matrix norms “induced” > ≠ by vector norms: x 0 if x 0 Ax Ax γ = γ ⋅ γ = x x for any scalar A max ≠ x x 0 + + ≤ ≤ + + x x y y x x y y (triangle inequality) (triangle inequality) � 1-norm: n ∑ = A max A (max absolute column sum) ij � These properties define a vector norm � These properties define a vector norm 1 j j i = i 1 1 � ∞ -norm: n ∑ ∞ = A max A (max absolute row sum) ij i i j = 1

Properties of Matrix Norms p Condition Number � If A is square and nonsingular, then � If A is square and nonsingular, then � These induced matrix norms satisfy: � These induced matrix norms satisfy: A − = ⋅ 1 A > ≠ cond( ) A A 0 if A 0 � If A is singular, then cond( A ) = ∞ � If A is singular then cond( A ) = ∞ γ = γ ⋅ γ A A for any scalar � If A is nearly singular, then cond( A ) is large. + + ≤ ≤ + + A A B B A A B B (triangle inequality) (triangle inequality) � The condition number measures the ratio of � The condition number measures the ratio of maximum stretch to maximum shrinkage: ≤ ⋅ AB A B − 1 ⎛ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎞ Ax A A Ax ≤ ⋅ ⋅ − = ⋅ 1 ⎜ ⎟ ⎜ ⎟ Ax A x for any vector x A A max min ⎜ ⎟ ⎜ ⎟ ≠ ≠ ⎝ x ⎠ ⎝ x ⎠ x 0 x 0 Errors and Residuals Properties of Condition Number � For any matrix A , cond( A ) ≥ 1 � For any matrix A cond( A ) ≥ 1 � Residual for an approximate solution y to � Residual for an approximate solution y to Ax = b is defined as r = b – Ay � For the identity matrix, cond( I ) = 1 � If A is nonsingular, then || x – y|| = 0 if and only g , || y|| y � For any permutation matrix, cond( P ) = 1 F t ti t i d( P ) 1 if || r || = 0. � For any scalar α , cond( α A ) = cond( A ) � Does not imply that if ||r||< ε , then ||x-y|| is small. � For any diagonal matrix D , ( ( ) ( ) ( ) ) = cond( cond( D D ) ) max max D D / min / min D D ii ii

Estimating Accuracy g y � Let x be the solution to Ax = b � Let x be the solution to Ax = b � Let y be the solution to Ay = c � Then a simple analysis shows that Th i l l i h th t − − x y b c ≤ ≤ cond( ) cond( ) A A x c � Errors in the data (b) are magnified by � Errors in the data (b) are magnified by cond(A ) � Likewise for errors in A � Likewise for errors in A