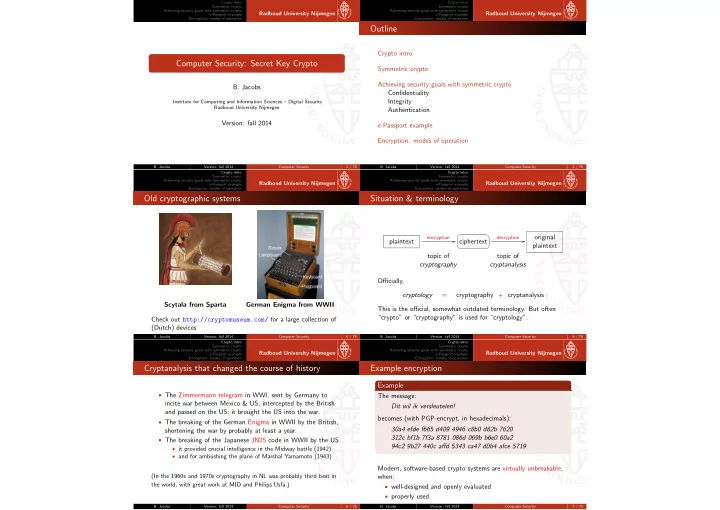
Outline Crypto intro Computer Security: Secret Key Crypto - PowerPoint PPT Presentation

� � Crypto intro Crypto intro Symmetric crypto Symmetric crypto Achieving security goals with symmetric crypto Achieving security goals with symmetric crypto Radboud University Nijmegen Radboud University Nijmegen e-Passport example e-Passport example Encryption: modes of operation Encryption: modes of operation Outline Crypto intro Computer Security: Secret Key Crypto Symmetric crypto Achieving security goals with symmetric crypto B. Jacobs Confidentiality Integrity Institute for Computing and Information Sciences – Digital Security Radboud University Nijmegen Authentication Version: fall 2014 e-Passport example Encryption: modes of operation B. Jacobs Version: fall 2014 Computer Security 1 / 75 B. Jacobs Version: fall 2014 Computer Security 2 / 75 Crypto intro Crypto intro Symmetric crypto Symmetric crypto Achieving security goals with symmetric crypto Achieving security goals with symmetric crypto Radboud University Nijmegen Radboud University Nijmegen e-Passport example e-Passport example Encryption: modes of operation Encryption: modes of operation Old cryptographic systems Situation & terminology ☛ ✟ original encryption decryption plaintext ciphertext plaintext ✡ ✠ topic of topic of cryptography cryptanalysis Officially, cryptology = cryptography + cryptanalysis Scytala from Sparta German Enigma from WWII This is the official, somewhat outdated terminology. But often “crypto” or “cryptography” is used for “cryptology”. Check out http://cryptomuseum.com/ for a large collection of (Dutch) devices B. Jacobs Version: fall 2014 Computer Security 4 / 75 B. Jacobs Version: fall 2014 Computer Security 5 / 75 Crypto intro Crypto intro Symmetric crypto Symmetric crypto Achieving security goals with symmetric crypto Achieving security goals with symmetric crypto Radboud University Nijmegen Radboud University Nijmegen e-Passport example e-Passport example Encryption: modes of operation Encryption: modes of operation Cryptanalysis that changed the course of history Example encryption Example • The Zimmermann telegram in WWI, sent by Germany to The message: incite war between Mexico & US, intercepted by the British Dit wil ik versleutelen! and passed on the US; it brought the US into the war. becomes (with PGP-encrypt, in hexadecimals): • The breaking of the German Enigma in WWII by the British, 30a4 efde f665 d409 4946 c8b0 d82b 7620 shortening the war by probably at least a year. 312c bf1b 7f3a 8781 086d 069b b6e0 60a2 • The breaking of the Japanese JN25 code in WWII by the US 94c2 9b27 440c affd 5343 ca47 d0b4 afce 5719 • it provided crucial intelligence in the Midway battle (1942) • and for ambushing the plane of Marshal Yamamoto (1943) Modern, software-based crypto systems are virtually unbreakable, (In the 1960s and 1970s cryptography in NL was probably third best in when: the world, with great work at MID and Philips Usfa.) • well-designed and openly evaluated • properly used B. Jacobs Version: fall 2014 Computer Security 6 / 75 B. Jacobs Version: fall 2014 Computer Security 7 / 75

Crypto intro Crypto intro Symmetric crypto Symmetric crypto Achieving security goals with symmetric crypto Achieving security goals with symmetric crypto Radboud University Nijmegen Radboud University Nijmegen e-Passport example e-Passport example Encryption: modes of operation Encryption: modes of operation Crypto system Ordering crypto primitives via numbers of keys The en/de-cryption is done with:  algorithm  crypto system number = + name key names notation of keys (or secret code, or cipher)  key (parameter of the algorithm) 0 hash functions — h ( m ) 1 symmetric crypto shared, secret K { m } Kerckhoffs principle asymmetric crypto public & private The strength of the crypto system must rely solely on the strength 2 { m } K (or public key crypto) keypair of the key; the algorithm must be (assumed to be) public. Modern interpretation of this principle: We start with symmetric key crypto. • Algorithm must arise from public competition (organised by NIST for AES & next hash) • Non-public algorithms must be distrusted (think of DVD-encryption, GSM, Mifare, . . . , all broken) B. Jacobs Version: fall 2014 Computer Security 8 / 75 B. Jacobs Version: fall 2014 Computer Security 9 / 75 Crypto intro Crypto intro Symmetric crypto Symmetric crypto Achieving security goals with symmetric crypto Achieving security goals with symmetric crypto Radboud University Nijmegen Radboud University Nijmegen e-Passport example e-Passport example Encryption: modes of operation Encryption: modes of operation First a few words on . . . words Alphabets In principle, an alphabet is an arbitrary set A . In this context, the elements a ∈ A are called letters. In practice, an alphabet is a finite set A = { a 1 , . . . , a n } of letters. Examples: • Crypto systems transform plaintext to cipher text • A = { 0 , 1 } , the alphabet of bits • They transform words to words • A = { a , b , c , . . . , z } , the alphabet of lowercase Latin • Words (aka. strings) are sequences of letters, taken from an characters; alphabet. • A = { 00 , 01 , . . . , 7 F } the ASCII alphabet, as hexadecimals; (Recall: 7 F = 127 = 2 7 − 1.) • The extended ASCII alphabet of 256 characters • UTF alphabets involve even more characters (depending on version, like UTF-16, UTF-32) B. Jacobs Version: fall 2014 Computer Security 10 / 75 B. Jacobs Version: fall 2014 Computer Security 11 / 75 Crypto intro Crypto intro Symmetric crypto Symmetric crypto Achieving security goals with symmetric crypto Achieving security goals with symmetric crypto Radboud University Nijmegen Radboud University Nijmegen e-Passport example e-Passport example Encryption: modes of operation Encryption: modes of operation Words Symmetric crypto: three basic techniques A word over an alphabet A is a finite sequence w = a 1 a 2 · · · a n of Suppose we have a message/word m and wish to (symmetrically) letters a i ∈ A . The length of this w is n , obviously. encrypt it to K { m } , using key K . There are three basic techniques: One writes A ⋆ for the set of words over A (aka. the Kleene star) 1 Substitution: exchange characters from the alphabet, like in For instance, { 0 , 1 } ⋆ is the set of binary words. Caesar’s cipher. The key K is: the character substitution/exchange function We write | , or sometimes just a comma, for concatenation of 2 Transposition: exchange positions of characters, words. Hence: block-by-block. � � b 1 b 2 · · · b m a 1 a 2 · · · a n = a 1 a 2 · · · a n b 1 b 2 · · · b m . The key K is: the position exchange function 3 One-time-pad: take bitwise XOR with keystream, for binary On binary words with the same length we write ⊕ for bitwise XOR: messages only. � � � � a 1 a 2 · · · a n ⊕ b 1 b 2 · · · b n The key K is: the keystream, which must have at least the = ( a 1 XOR b 1 )( a 2 XOR b 2 ) · · · ( a n XOR b n ) . same length as the message Encryption/decryption are functions from words to words Ciphers like DES and AES involve repeated combinations of (usually binary). substitution and transposition, depending on a secret key B. Jacobs Version: fall 2014 Computer Security 12 / 75 B. Jacobs Version: fall 2014 Computer Security 14 / 75