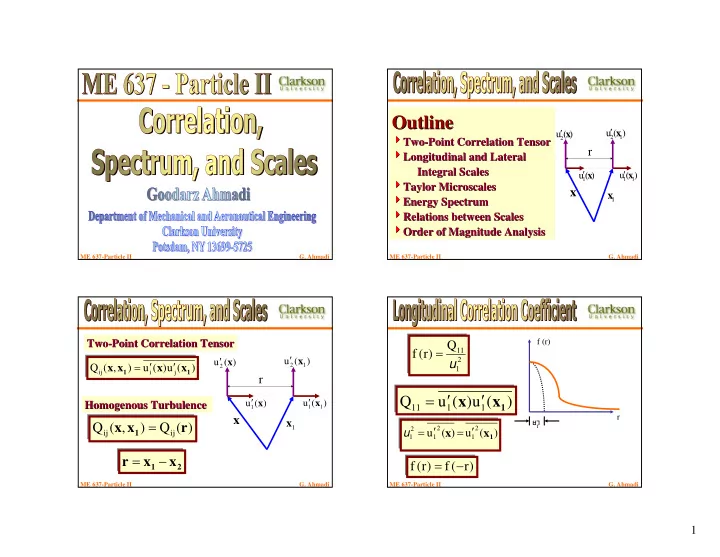
Outline Outline u 2 x ( ) u 2 x ( ) 4 Two 4 1 Two- - PowerPoint PPT Presentation

Outline Outline ′ ′ u 2 x ( ) u 2 x ( ) 4 Two 4 1 Two- -Point Correlation Tensor Point Correlation Tensor r 4 Longitudinal and Lateral 4 Longitudinal and Lateral Integral Scales Integral Scales ′ ′ u 1 x ( ) u 1 x ( ) 1 4 Taylor 4 Taylor Microscales Microscales x x 4 Energy Spectrum 4 1 Energy Spectrum 4 Relations between Scales 4 Relations between Scales 4 Order of Magnitude Analysis 4 Order of Magnitude Analysis ME 637-Particle II G. Ahmadi ME 637-Particle II G. Ahmadi Two- -Point Correlation Tensor Point Correlation Tensor f (r) Two Q = 11 f ( r ) ′ ′ u 2 x ( ) 2 u 2 x ( ) = ′ ′ u 1 Q ( x , x ) u ( x ) u ( x ) 1 ij 1 i j 1 r ′ ′ = x x ′ ′ Q u ( ) u ( ) u 1 x ( ) u 1 x ( ) Homogenous Turbulence Homogenous Turbulence 11 1 1 1 1 r x 8 1 = x Q ( x , x ) Q ( r ) ′ ′ = = f 1 2 2 2 u ( x ) u ( x ) ij ij u 1 1 1 1 = − r x x = − f ( r ) f ( r ) 1 2 ME 637-Particle II G. Ahmadi ME 637-Particle II G. Ahmadi 1

Lateral g (r) Lateral Longitudinal Q Longitudinal = 22 g ( r ) Microscale Microscale Microscale Microscale 2 u 2 2 2 λ = − λ = − 2 2 ′ ′ = ′ ′ Q u ( x ) u ( x ) ′ ′ g f g ( 0 ) f ( 0 ) 22 2 2 1 r 8 g = − 2 1 r g ( r ) g ( r ) ′ ′ = + + ≈ − 2 L g ( r ) 1 r g ( 0 ) 1 λ 2 2 ! g ME 637-Particle II G. Ahmadi ME 637-Particle II G. Ahmadi ′ ′ + τ u ( x , t ) u ( x , t ) τ = ∞ 1 1 R ( ) ∫ E 2 Longitudinal Longitudinal Λ = u f ( r ) dr 1 f Macroscale Macroscale Macroscale Microscale Macroscale Microscale 0 ∞ 2 τ = − ∫ 2 = τ τ T R ( ) d ′ ′ E E E ∞ R ( 0 ) E 0 ∫ Λ = Lateral Lateral g ( r ) dr Frozen Field Approximation Frozen Field Approximation g Macroscale Macroscale ∂ ∂ Λ ≈ λ ≈ U τ 0 = − UT U f E f E ∂ ∂ t x τ ≈ E τ f ( U ) R ( ) ME 637-Particle II G. Ahmadi ME 637-Particle II G. Ahmadi 2

′ ′ + τ +∞ +∞ +∞ v ( t ) v ( t ) τ = 1 L L ∫ ∫ ∫ R ( ) − k ⋅ = i x E ( k ) Q ( x ) e dx L ′ 2 π v ij ij 3 8 L − ∞ − ∞ − ∞ Lagrangian Lagrangian Lagrangian Time Lagrangian Time +∞ +∞ +∞ Time Microscale Time Microscale Macroscale Macroscale ∫ ∫ ∫ − k ⋅ = i x Q ( x ) E ( k ) e dk ∞ ij ij 2 τ = − ∫ 2 = τ τ − ∞ − ∞ − ∞ T R ( ) d ′ ′ L L L R ( 0 ) L 0 ME 637-Particle II G. Ahmadi ME 637-Particle II G. Ahmadi +∞ 2 u ∫ = − ik x 1 E ( k ) f ( x ) e dx 1 1 f (r) π l 1 1 1 Λ E(k 1 ) 2 2 = u − ∞ 1 f E ( k ) 1 1 π + Λ r 2 2 1 k − f 1 = Λ f ( r ) e f +∞ 1 ∫ = 2 ik x u f ( x ) E ( k ) e dk 1 1 1 1 1 1 1 2 − ∞ k 1 ∞ ∞ r 2 2 u ∫ ∫ = = 2 1 E ( k ) f ( x ) cos k x dx u f ( x ) E ( k ) cos k x dk π 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 ME 637-Particle II G. Ahmadi ME 637-Particle II G. Ahmadi 3

′ ′ ∂ ∂ Energy Macroscopic 3 2 Energy u u Macroscopic u u ε = ν ε = = ν i i A 30 ∂ ∂ Λ λ Dissipation Estimate Dissipation Estimate 2 x x j j f ′ ∂ u Isotropic Isotropic λ ε = ν = − ν ′ ′ ′ 2 2 1 30 15 ( ) 15 u f ( 0 ) λ − = Λ f << 1 / 2 ∂ f u 1 R x = >> Λ 1 Turbulence Turbulence Λ R 1 Λ 1 A Λ ν ′ 2 2 2 u u u ε = ν = ν = ν λ λ λ 1 u 30 30 15 15 15 = λ λ λ 2 2 2 = − = − g 1 / 2 g 1 R R R λ λ ν f f g Λ Λ Λ A A λ = λ 2 f g ME 637-Particle II G. Ahmadi ME 637-Particle II G. Ahmadi Deformation Rate Tenor Taylor- -Kolmogorov Kolmogorov Deformation Rate Tenor Taylor Velocity Gradient Velocity Gradient ′ ′ ′ ′ λ ∂ ∂ ε ∂ ∂ u u u u u u 225 ′ ′ = = Λ = 2 i i 2 g 1 / 4 1 / 4 1 / 4 1 / 2 i i ~ ( ) d d ~ ~ ( ) ( ) R 15 R λ ∂ ∂ ν λ ∂ ∂ λ ij ij η x x x x A j j j j Viscosity Viscosity Kolmogorov- Kolmogorov -Time Scale Time Scale λ 2 3 2 ~ u ε η ν u u u 0 . 26 ν ν = = ~ τ = = 0 . 26 Λ λ Λ 2 λ ν τ υ ε g ME 637-Particle II G. Ahmadi ME 637-Particle II G. Ahmadi 4

Taylor/Integral Taylor/Integral Kolmogorov/Integral Kolmogorov/Integral Concluding Remarks Concluding Remarks λ η 4 Two 4 − − Two- -Point Correlation Tensor Point Correlation Tensor − − 3 / 4 3 / 2 1 / 2 1 ~ R ~ R ~ R ~ R Λ λ Λ λ Λ Λ 4 Longitudinal and Lateral Scales 4 Longitudinal and Lateral Scales 4 Integral Scales 4 Integral Scales Kolmogorov/Taylor Kolmogorov/Taylor Different Scales Different Scales 4 Taylor 4 Taylor Microscales Microscales η 4 Energy Spectrum 4 Energy Spectrum η Λ = λ − − 2 3 1 / 4 1 / 2 ~ R ~ R 4 Relations between Scales 4 Λ λ λ Relations between Scales 4 Order of Magnitude Analysis 4 Order of Magnitude Analysis ME 637-Particle II G. Ahmadi ME 637-Particle II G. Ahmadi ME 637-Particle II G. Ahmadi 5