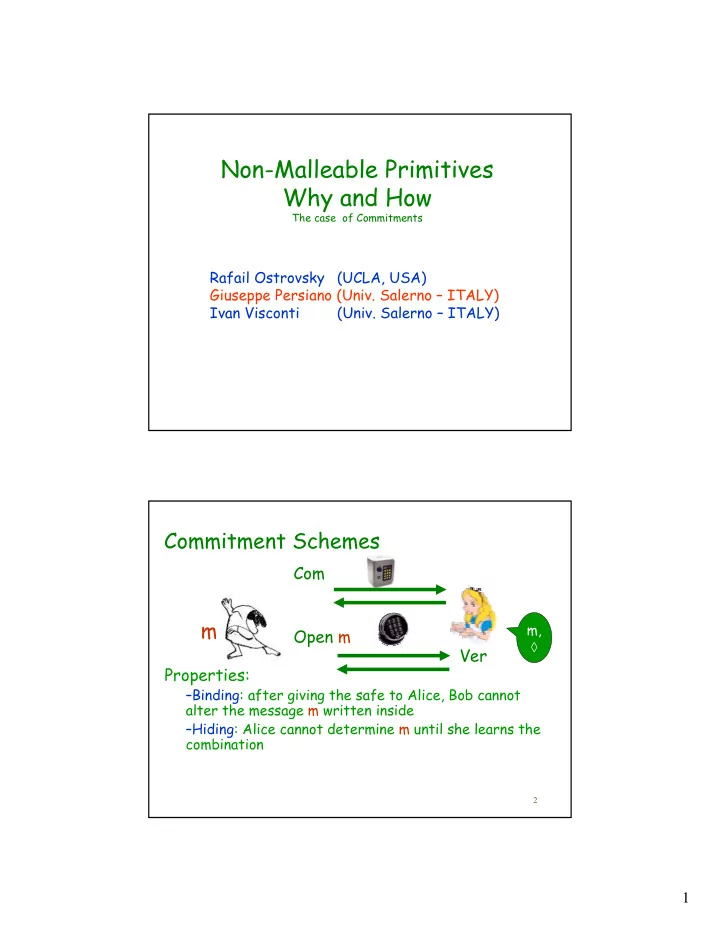

Non-Malleable Primitives Why and How The case of Commitments Rafail Ostrovsky (UCLA, USA) Giuseppe Persiano (Univ. Salerno – ITALY) Ivan Visconti (Univ. Salerno – ITALY) Commitment Schemes Com m m, Open m ◊ Ver Properties: –Binding: after giving the safe to Alice, Bob cannot alter the message m written inside –Hiding: Alice cannot determine m until she learns the combination 2 1
Commitment Schemes Com m m, Open m ◊ Ver Properties: – Statitical Binding: there is no way to open Com in two different ways 3 Commitment Schemes Com m m, Open m ◊ Ver Properties: –Statistical Hiding: actually the transcript of the commitment phase does not encode any specific message (in the information theoretic sense), thus Com can be potentially opened to any message 4 2
Commitment Schemes Com m m, Open m ◊ Ver Very useful, but often we need more..... 5 Auction Phase I: commit to bid b 1 Com 1 b 2 Com 2 6 3
Auction Phase II: reveal bid Open b 1 Open b 2 7 Man-in-the-Middle (MiM) Attack Com m Com’ Open m Open m’ m m and m’ could be related 8 4
Man-in-the-Middle (MiM) Attack we should define commitment schemes that remain secure under such attacks 9 Non-Malleable Commitments with respect to commitment: • the message m’ encoded in the commitment of MiM should not be related to the message m encoded in the commitment of the sender • it does make sense in case of statistical binding • it does not make sense in case of statistical hiding with respect to opening: • the MiM Adversary should not be able to produce a commitment such that the message m’ opened by MiM is related to the message m opened by the committer • it does make sense in case of statistical binding • it does make sense in case of statistical hiding 10 5
State-of-the-Art (constant round) NM commitments with respect to commitment: • C ommon R eference S tring model: of course! [several papers] • Plain model: [PR05] (non - b lack- b o x techniques); NM commitments with respect to opening: • CRS model: of course! [many papers] • Plain model: [PR05] (non - b lack- b o x techniques); 11 Our Setting: the Plain Model We focus on: constant - r ound NM commitments in the plain model… … therefore we consider the [PR05] paper We are still discussing the definitions, therefore let’s give a more careful look at the [PR05] definitions and results 12 6
Statistically Hiding NM Commitments with respect to opening [PR05] Junk View m’ m m is known to the simulator just before the <real game> decommitment phase 13 Statistically Binding NM Commitments with respect to commitment [PR05] <Junk> View m’ <real game> no opening ?? 14 7
Statistically Hiding NM Commitments with respect to opening [PR05] <Junk> View m’ m m is known to the simulator just before the <real game> decommitment phase 15 Statistically Binding NM Commitments with respect to commitment [PR05] <Junk> View m’ <real game> no opening ?? 16 8
Statistically Binding NM Commitments [ derived from PR05] with respect to opening <Junk> View m’ m m is known to the simulator just before the <real game> decommitment phase 17 Statistically Binding NM Commitments [ derived from PR05] with respect to opening <Junk> View m’ m now the simulator should also be able to open to m the committed junk 18 9
Ok let’s look at the PR05 construction Commitment Phase: C � R send a statistically binding commitment of m C � R use a statistical NMZK argument of knowledge for proving knowledge of the committed message Decommitment Phase: C � R open the commitment of m Simulator : it commits to junk and uses the simulator of NMZK argument of knowledge. No way of opening the commitment of junk to a given message! 19 Ok let’s look at the PR05 construction Commitment Phase: C � R send a statistically binding commitment of m C � R use a statistical NMZK argument of knowledge for proving knowledge of the committed message Decommitment Phase: C � R open the commitment of m 20 10
Statistically Hiding NM w.r.t opening Commitment Phase: C � R send a statistically hiding commitment of m Decommitment Phase: C � R send m C � R use a statistical NMZK argument of knowledge for proving that m is the committed message Simulator : it commits to junk and during the decommitment phase it uses the simulator of NMZK argument of knowledge. 21 Statistically Hiding NM w.r.t opening Commitment Phase: C � R send a statistically hiding commitment of m Decommitment Phase: C � R send m C � R use a statistical NMZK argument of knowledge for proving that m is the committed message 22 11
Our commitment (based on [PR05] constructions): NM both with respect to commitment and to opening Commitment Phase: C � R send a statistically binding commitment of m C � R use a statistical NMZK argument of knowledge for proving knowledge of the committed message Decommitment Phase: C � R send m C � R use a statistical NMZK argument of knowledge for proving that m is the committed message Simulator: it commits to junk and uses twice the simulator of the NMZK argument of knowledge. 23 Concurrent Man-in-the-Middle (MiM) Attack <Com> <Com’> <m> <Open> <m> <Open> <m’> <m> <m> and <m’> could be related 24 12
Auction on the Internet � Same MIM Adversary maybe involved in several concurrent auctions � Still want commitments be independent from the ones of other players 25 Statistically Binding Concurrent NM Commitments with respect to commitment [PR05b] <Junk> View <m’> no opening ?? 26 13
Let’s look at the PR05b construction Commitment Phase: C � R send a statistically binding commitment of m C � R use a statistical NMZK argument of knowledge for proving knowledge of the committed message Decommitment Phase: C � R open the commitment of m 27 Let’s look at the PR05b construction Commitment Phase: C � R send a statistically binding commitment of m C � R use a statistical NMZK argument of knowledge for proving knowledge of the committed message Decommitment Phase: C � R open the commitment of m let’s try again our fix for the standalone case, maybe it works again… 28 14
Our commitment (based on [PR05] constructions): NM both with respect to commitment and to opening Commitment Phase: C � R send a statistically binding commitment of m C � R use a statistical NMZK argument of knowledge for proving knowledge of the committed message Decommitment Phase: C � R send m C � R use a statistical NMZK argument of knowledge for proving that m is the committed message Simulator: it commits to junk and uses twice the simulator of the NMZK argument of knowledge. WHEN CONCURRENCY IS ALLOWED, THE SIMULATOR DOES NOT WORK ANYMORE !!! 29 Our commitment (based on [PR05] constructions): NM both with respect to commitment and to opening Commitment Phase: C � R send a statistically binding commitment of m C � R use a statistical NMZK argument of knowledge for proving knowledge of the committed message Decommitment Phase: C � R send m C � R use a statistical NMZK argument of knowledge for proving that m is the committed message Simulator: it commits to junk and uses twice the simulator of the NMZK argument of knowledge. In [PR05b] there is no concurrent NM commitment with respect to opening, thus there is no additional technique that can be exploited for a new fix !!! 30 15
Our commitment (based on [PR05] constructions): NM both with respect to commitment and to opening Commitment Phase: C � R send a statistically binding commitment of m C � R use a statistical NMZK argument of knowledge for proving knowledge of the committed message Decommitment Phase: C � R send m C � R use a statistical NMZK argument of knowledge for proving that m is the committed message m Simulator: it commits to junk and uses twice the simulator of the NMZK argument of knowledge. Concurrent NM commitment with respect to opening is actually left as an important open problem by PR05b !!! 31 Our Result We show: a constant- r ound concurrent NM commitment scheme in the plain model… the scheme is NM both with respect to commitment and with respect to opening 32 16
Our Commitment Scheme Commitment Phase: R � C send TWO statistically binding commitments of random messages r,s R � C use a statistical NMZK argument of knowledge for proving knowledge of one of the two committed messages C � R send a statistically binding commitment Com of m C � R use a statistical NMZK argument of knowledge for proving knowledge of the committed message 33 Our Commitment Scheme Decommitment Phase: R � S open r and s C � R send m C � R use a statistical NMZK argument of knowledge for proving that m is the committed message in Com OR r is the committed message in Com OR s is the committed message in Com 34 17
Properties Binding. By the statistical binding of the used commitment scheme, and by the soundness of the NMZK argument system, the binding property can only by violated if the prover committed to either r or s. However this can be reduced for breaking the hiding property of the commitment scheme. 35 Properties Hiding. It follows from the statistical ZK property and from the hiding of the used commitment scheme. 36 18
Recommend
More recommend