Multiple change-point analysis k k k f s g f h g - PDF document

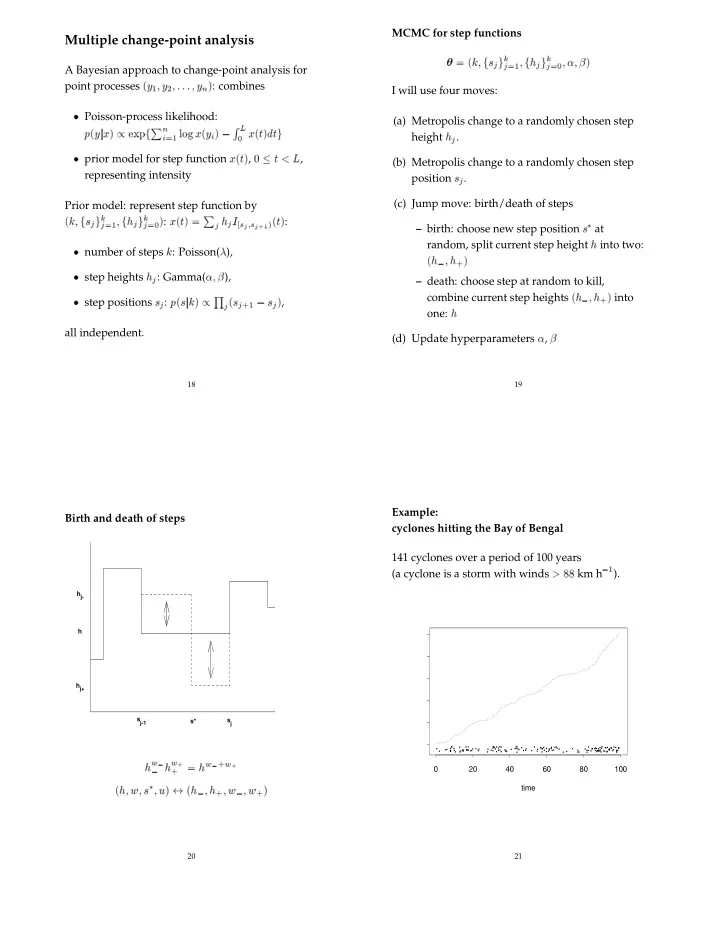
MCMC for step functions Multiple change-point analysis k k � � k � f s g � f h g � � � � � � j j j �� j �� A Bayesian approach to change-point analysis for � y � y � � � � � y � : combines point processes � � n I will use four moves: � Poisson-process likelihood: (a) Metropolis change to a randomly chosen step L n R p � y j x � � exp f P log x � y � � x � t � dt g height h j . i i �� � � prior model for step function x � t � , � � t � L , (b) Metropolis change to a randomly chosen step representing intensity position s j . (c) Jump move: birth/death of steps Prior model: represent step function by k k � k � f s g � f h g � : x � t � � P h I � t � : � at j j j � s � j �� j �� �s j j j �� – birth: choose new step position s random, split current step height h into two: � number of steps k : Poisson( � ), � h � h � � � � step heights h j : Gamma( � � � ), – death: choose step at random to kill, combine current step heights � h � h � into � step positions s j : p � s j k � � Q � s � s � , � � j �� j j one: h all independent. (d) Update hyperparameters � , � 18 19 Example: Birth and death of steps cyclones hitting the Bay of Bengal 141 cyclones over a period of 100 years � � ). (a cyclone is a storm with winds � �� km h h j- h h j+ s j-1 s j s* . .. ... .. . . . .. . .. . . . ... .. .. .. .. . .. . ... .. . . .... .. . . .. .. . .... . . . . . . . . .. . .. . .. . ... . . ... . . . . . .. . .. . . . . .. . . .. . . .. . .. . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . w w w � w h h � � h � � 0 20 40 60 80 100 � � � � � h� w � s � u � � � h � h � w � w � time � � � � 20 21

Choices of hyperparameters: Posterior for the number of change points k � Prior on k : Poisson( � ), with � � � . � Prior on h j : Gamma( � , � ), with – � � ��� � �� – � � ��� � n�L � o o Sample of step functions from the posterior: 0.20 probability o o 0.10 o 3 o o o 0.0 o o o o o intensity 2 0 2 4 6 8 10 12 1 k 0 Zero change points is ruled out; k � � or � more 0 20 40 60 80 100 probable than under the prior. time 22 23 Model-averaged estimate: E � x � � � j y � Posterior density estimates for change-point positions 2.5 2.0 1.5 0.15 intensity 1.0 0.10 density 0.5 0.0 . .. .. ... . . .. . ... .... . ... .. . . .. . .. .. .... . . .. . . . . . . . .. . . . .. . ... .. . . . . .. . . . .. . . .. . .. . . . . . .. . . .. . . 0.05 .. . . .. . . .. .. . . .. . . . . . . ... . . . . . . .. . . . . . . . . . . . . . . 0 20 40 60 80 100 0.0 time 0 20 40 60 80 100 time (the expectation of a random step function is not a step function). 24 25

Ordinary smoothing methods (in this case a kernel smoother) can’t match that mean curve 2.5 2.0 1.5 intensity 1.0 0.5 0.0 .. . .. . ... . . . .. .. .... . . . .. . . ... .. . . . .. . . . ... . .... . . .. . .. . .. .. . . .. . . . .. . . .. .. . .. . .. . ... .. ... . ... . .. . . . . . . . . .. . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . 0 20 40 60 80 100 time – fixed-bandwidth smoothers either over-smooth the steps, or under-smooth the plateaux. 26