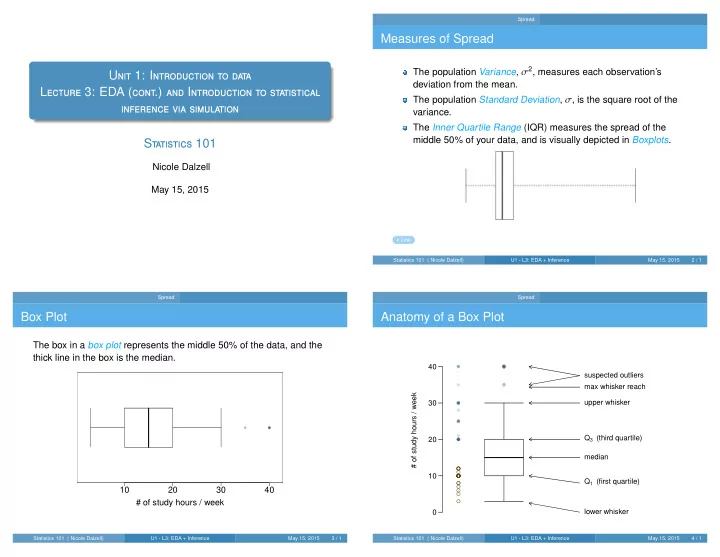

Spread Measures of Spread The population Variance , σ 2 , measures each observation’s U nit 1: I ntroduction to data deviation from the mean. L ecture 3: EDA ( cont .) and I ntroduction to statistical The population Standard Deviation , σ , is the square root of the inference via simulation variance. The Inner Quartile Range (IQR) measures the spread of the middle 50% of your data, and is visually depicted in Boxplots . S tatistics 101 Nicole Dalzell May 15, 2015 Link Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 2 / 1 Spread Spread Box Plot Anatomy of a Box Plot The box in a box plot represents the middle 50% of the data, and the thick line in the box is the median. 40 suspected outliers max whisker reach # of study hours / week upper whisker 30 Q 3 (third quartile) 20 median 10 Q 1 (first quartile) 10 20 30 40 # of study hours / week lower whisker 0 Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 3 / 1 Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 4 / 1
Spread Spread Measures of Location Whiskers and Outliers The 25 th percentile is also called the first quartile, Q1 . Whiskers of a box plot can extend up to 1.5 * IQR away from the The 50 th percentile is also called the median. quartiles. The 75 th percentile is also called the third quartile, Q3 . max upper whisker reach : Q 3 + 1 . 5 ∗ IQR = 20 + 1 . 5 ∗ 10 = 35 summary( d$study hours ) max lower whisker reach : Q 1 − 1 . 5 ∗ IQR = 10 − 1 . 5 ∗ 10 = − 5 Min . 1 st Qu. Median Mean 3rd Qu. Max. NAs 3.00 10.00 15.00 17.42 20.00 40.00 13.00 An outlier is defined as an observation beyond the maximum Between Q1 and Q3 is the middle 50% of the data. The range these reach of the whiskers. It is an observation that appears extreme data span is called the interquartile range , or the IQR . relative to the rest of the data. IQR = 20 − 10 = 10 Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 5 / 1 Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 6 / 1 Spread Spread Outliers (cont.) Why visualize? What does a response of 0 mean in this distribution? Why is it important to look for outliers? Number of drinks it takes students to get drunk Identify extreme skew in the distribution. Identify data collection and entry errors. ● ● Provide insight into interesting features of the data. 0 2 4 6 8 10 12 Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 7 / 1 Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 8 / 1
Spread Robust Statistics Spread Robust Statistics Extreme observations Income Example ● How would sample statistics such as mean, median, SD, and IQR of ● ● ● ● ● ● household income be affected if the largest value was replaced with ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● $10 million? What if the smallest value was replaced with $10 million? ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 0 200 400 600 800 1000 ● ● ● household income ($ thousands) ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● robust not robust scenario median IQR ¯ x s 0 200 400 600 800 1000 original data 165K 150K 211K 180K household income ($ thousands) move largest to $10 million 165K 150K 398K 1,422K move smallest to $10 million 190K 163K 4,186K 1,424K Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 9 / 1 Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 10 / 1 Spread Robust Statistics Spread Robust Statistics Robust statistics Range and IQR Range Range of the entire data. Since the median and IQR are more robust to skewness and outliers than mean and SD: range = max − min skewed → median and IQR symmetric → mean and SD IQR Range of the middle 50% of the data. If you were searching for a car, and you are price conscious, would you be more interested in the mean or median vehicle price when con- IQR = Q 3 − Q 1 sidering a car? Is the range or the IQR more robust to outliers? Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 11 / 1 Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 12 / 1
Spread Robust Statistics Spread Robust Statistics Example: Visualizing Who uses the most energy? What does our Energy Data look like? Country.Name X2011 1 Iceland 17964.44 Energy Use Data Boxplot 2 Qatar 17418.69 3 Trinidad and Tobago 15691.29 4 Kuwait 10408.28 15000 5 Brunei Darussalam 9427.09 6 Oman 8356.29 7 Luxembourg 8045.90 Energy Usage 8 United Arab Emirates 7407.01 10000 9 Bahrain 7353.16 10 Canada 7333.28 11 North America 7062.22 5000 12 United States 7032.35 13 Saudi Arabia 6738.42 14 Singapore 6452.33 15 Finland 6449.04 0 Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 13 / 1 Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 14 / 1 Spread Robust Statistics Spread Robust Statistics Participation question Side-by-side box plot Which of the following is false about the distribution of average number How does the number of the average number of times students go of hours students study daily? out per week vary by involvement? Do the two variables appear to be associated or independent? Average number of hours students study daily 5 ● ● ● 4 2 4 6 8 10 3 ● Min. 1st Qu. Median Mean 3rd Qu. Max. 2 ● 1.000 3.000 4.000 3.821 5.000 10.000 1 (a) There are no students who don’t study at all. (b) 75% of the students study more than 5 hours daily, on average. 0 ● ● ● (c) 25% of the students study less than 3 hours, on average. Greek Independent SLG (d) IQR is 2 hours. Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 15 / 1 Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 16 / 1
Spread Robust Statistics Spread Deviation Measures of Spread Deviation The distance of an observation from the mean is its deviation : x i − ¯ x . The population Variance , σ 2 , measures each observation’s deviation from the mean. sort ( d$sleep ) The population Standard Deviation , σ , is the square root of the [ 1 ] 1 1 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 variance. [30] 4 4 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 [59] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 6 6 7 7 7 7 7 7 7 7 8 9 9 9 The Inner Quartile Range (IQR) measures the spread of the mean( d$sleep ) middle 50% of your data, and is visually depicted in Boxplots . [ 1 ] 4.6 x 1 − ¯ x = 1 − 4 . 6 = − 3 . 6 x 2 − ¯ x = 1 − 4 . 6 = − 3 . 6 x 3 − ¯ x = 2 − 4 . 6 = − 2 . 6 . . . x 86 − ¯ x = 9 − 4 . 6 = 4 . 4 Link Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 17 / 1 Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 18 / 1 Spread Deviation Spread Deviation Variance Variance (cont.) Population Variance, σ 2 Why do we use the squared deviation in the calculation of variance? Roughly the average squared deviation from the mean To get rid of negatives so that observations equally distant from � N i = 1 ( x i − µ ) 2 the mean are weighed equally. σ 2 = To weigh larger deviations more heavily N Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 19 / 1 Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 20 / 1
Spread Deviation Spread Deviation Variance Notation Recap Sample Variance, s 2 Roughly the average squared deviation from the mean mean variance SD � n x ) 2 i = 1 ( x i − ¯ s 2 ¯ sample x s s 2 = n − 1 σ 2 population µ σ Given that the sample mean is 4.6, the sample variance of the hours Do you see a trend in what types of letters are used for sample of sleep students get per night can be calculated as: statistics vs. population parameters? s 2 = ( 1 − 4 . 6 ) 2 + ( 1 − 4 . 6 ) 2 + · · · + ( 9 − 4 . 6 ) 2 Latin letters for sample statistics, Greek letters for population = 2 . 76 86 − 1 parameters. Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 21 / 1 Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 22 / 1 Spread Deviation Spread Deviation Variability vs. diversity Which of the following sets of cars has more diverse composition of colors? Set 1: Application exercise: Variability Set 2: Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 23 / 1 Statistics 101 ( Nicole Dalzell) U1 - L3: EDA + Inference May 15, 2015 24 / 1
Recommend
More recommend