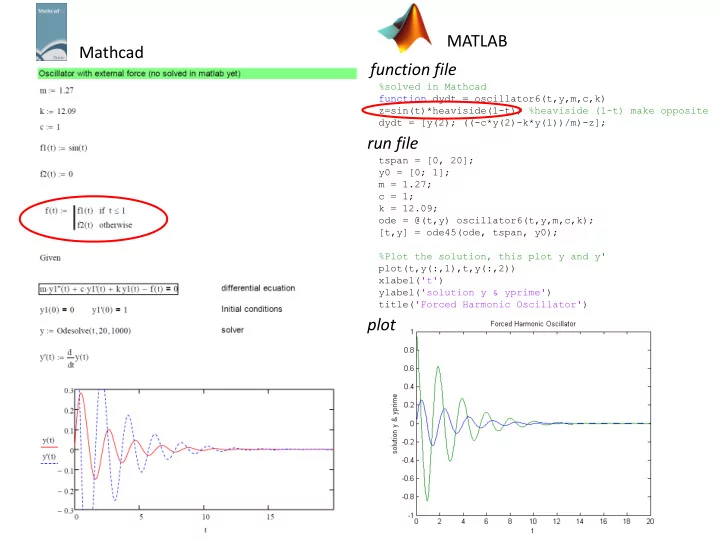
MATLAB Mathcad function file %solved in Mathcad function dydt = - PowerPoint PPT Presentation

MATLAB Mathcad function file %solved in Mathcad function dydt = oscillator6(t,y,m,c,k) z=sin(t)*heaviside(1-t); %heaviside (1-t) make opposite dydt = [y(2); ((-c*y(2)-k*y(1))/m)-z]; run file tspan = [0, 20]; y0 = [0; 1]; m = 1.27; c = 1; k = 12.09; ode = @(t,y) oscillator6(t,y,m,c,k); [t,y] = ode45(ode, tspan, y0); %Plot the solution, this plot y and y' plot(t,y(:,1),t,y(:,2)) xlabel('t') ylabel('solution y & yprime') title('Forced Harmonic Oscillator') plot

MATLAB Mathcad function file %solved in Mathcad function dydt = oscillator10(t,y,m,c,k) if ((t>=0) && (t<0.01)) a=(-1.27e-4*cos((4*pi*t)/0.02)+1.27e-4); else a=(1.27e-4*cos((4*pi*t)/0.02)-1.27e-4); end dydt = [y(2); (((-c*y(2)-k*y(1)))+(a))/m]; run file tspan = [0, 0.02]; y0 = [0; 0]; m = 1.27e-7; c = 0; k = 12.09; ode = @(t,y) oscillator10(t,y,m,c,k); [t,y] = ode45(ode, tspan, y0); %Plot the solution, this plot y and y' plot(t,y(:,1),t,y(:,1)) xlabel('t') ylabel('solution y & yprime') title('Harmonic Oscillator') plot

MATLAB Mathcad

MATLAB SIMULINK m=1.27; k=12.09; c=1; km=-k/m; cm=-c/m; Amp=1; Freq=1; y0=1;

MATLAB