Linear Classifier Linear classifiers are single layer neural - PowerPoint PPT Presentation

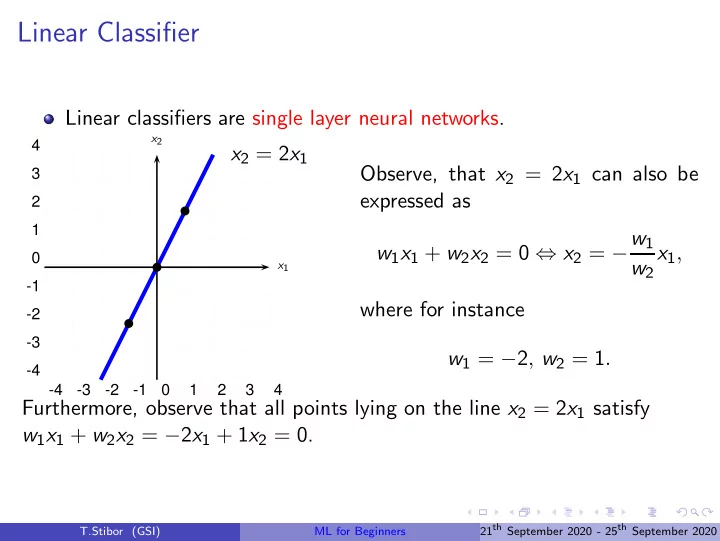
b b b Linear Classifier Linear classifiers are single layer neural networks. x 2 4 x 2 = 2 x 1 Observe, that x 2 = 2 x 1 can also be 3 expressed as 2 1 w 1 x 1 + w 2 x 2 = 0 ⇔ x 2 = − w 1 x 1 , 0 w 2 x 1 -1 where for instance -2 -3 w 1 = − 2 , w 2 = 1 . -4 -4 -3 -2 -1 0 1 2 3 4 Furthermore, observe that all points lying on the line x 2 = 2 x 1 satisfy w 1 x 1 + w 2 x 2 = − 2 x 1 + 1 x 2 = 0. 21 th September 2020 - 25 th September 2020 T.Stibor (GSI) ML for Beginners

b Linear Classifier & Dot Product x 2 − 2 x 1 + 1 x 2 = 0 4 3 What about the vector 2 x = (1 , 2) w = ( w 1 , w 2 ) = ( − 2 , 1)? w 1 Vector w is perpendicular to 0 x 1 the line − 2 x 1 + 1 x 2 = 0. -1 Let us calculate the dot -2 product of w and x . -3 -4 -4 -3 -2 -1 0 1 2 3 4 The dot product is defined as w 1 x 1 + w 2 x 2 + . . . + w d x d = w T · x def = � w , x � , for some d ∈ N . In our example d = 2 and we obtain − 2 · 1 + 1 · 2 = 0. 21 th September 2020 - 25 th September 2020 T.Stibor (GSI) ML for Beginners

b Linear Classifier & Dot Product (cont.) Let us consider the weight vector w = (3 , 0) and vector x = (2 , 2). x 2 4 3 3 x 1 + 0 x 2 = 0 2 x = (2 , 2) 1 0 x 1 w -1 � w , x � � w � = 3 · 2+0 · 2 = 2 √ 3 2 -2 -3 -4 -4 -3 -2 -1 0 1 2 3 4 Geometric interpretation of the dot product: Length of the projection of x onto the unit vector w / � w � . 21 th September 2020 - 25 th September 2020 T.Stibor (GSI) ML for Beginners

Dot Product as a Similarity Measure Dot product allows us to compute: lengths, angles and distances. Length (norm): � x � = x 1 x 1 + x 2 x 2 + . . . + x d x d = � x , x � √ √ 1 2 + 1 2 + 1 2 = Example: x = (1 , 1 , 1) we obtain � x � = 3 Angle: cos α = � w , x � w 1 x 1 + w 2 x 2 + . . . + w d x d � w �� x � = � � w 2 1 + w 2 2 + . . . + w 2 x 2 1 + x 2 2 + . . . + x 2 d d Example: w = (3 , 0), x = (2 , 2) we obtain cos α = � w , x � 3 · 2 + 0 · 2 2 � w �� x � = √ 3 2 + 0 2 √ 2 2 + 2 2 = √ 8 and obtain α = cos − 1 � � 2 = 0 . 7853982 and 0 . 7853982 · 180 /π = 45 ◦ √ 8 21 th September 2020 - 25 th September 2020 T.Stibor (GSI) ML for Beginners

Dot Product as a Similarity Measure (cont.) Distance (Euclidean): � � ( w 1 − x 1 ) 2 + ( w 2 − x 2 ) 2 dist ( w , x ) = � w − x � = � w − x , w − x � = Example: w = (3 , 0), x = (2 , 2) we obtain � � √ (3 − 2) 2 + (0 − 2) 2 = � w − x � = � w − x , w − x � = 5 Popular application in natural language processing: Dot product on text documents, in other words how similar are e.g. two given text documents. 21 th September 2020 - 25 th September 2020 T.Stibor (GSI) ML for Beginners

b b b b b Linear Classifier & Two Half-Spaces x 2 4 3 { x | − 2 x 1 + 1 x 2 > 0 } 2 w 1 0 x 1 -1 { x | − 2 x 1 + 1 x 2 < 0 } -2 -3 -4 -4 -3 -2 -1 0 1 2 3 4 { x | − 2 x 1 + 1 x 2 = 0 } The x -space is separated in two half-spaces. 21 th September 2020 - 25 th September 2020 T.Stibor (GSI) ML for Beginners

Linear Classifier & Dot Product (cont.) Observe, that w 1 x 1 + w 2 x 2 = 0 implies, that the separating line always goes through the origin. By adding an offset (bias), that is w 0 + w 1 x 1 + w 2 x 2 = 0 ⇔ x 2 = − w 1 w 2 x 1 − w 0 w 2 ≡ y = mx + b , one can shift the line arbitrary. x 2 x 2 4 4 3 3 2 2 1 1 0 0 x 1 x 1 -1 -1 -2 -2 -3 -3 -4 -4 -4 -3 -2 -1 0 1 2 3 4 -4 -3 -2 -1 0 1 2 3 4 w 0 + w 1 x 1 + w 2 x 2 = 0 w 0 + w 1 x 1 + w 2 x 2 > threshold 21 th September 2020 - 25 th September 2020 T.Stibor (GSI) ML for Beginners

b b b b b Linear Classifier & Single Layer NN x 2 Output f ( x ) 4 3 x 1 2 1 w 0 w 1 w d ⇔ 0 x 1 -1 x 0 x 1 x d -2 -3 Input -4 Note that x 0 = 1 , f ( x ) = � w , x � . -4 -3 -2 -1 0 1 2 3 4 Given data which we want to separate, that is, a sample X = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } ∈ R d +1 × {− 1 , +1 } . How to determine the proper values of w such that the “minus” and “plus” points are separated by f ( x )? Infer the values of w from the data by some learning algorithm. 21 th September 2020 - 25 th September 2020 T.Stibor (GSI) ML for Beginners

Perceptron Note, so far we have not seen a method for finding the weight vector w to obtain a linearly separation of the training set. Let f ( a ) be (sign) activation function � − 1 if a < 0 f ( a ) = +1 if a ≥ 0 and decision function � d � � f ( � w , x � ) = f w i x i . i =0 Note: x 0 is set to +1, that is, x = (1 , x 1 , . . . , x d ). Training pattern consists of ( x , y ) ∈ R d +1 × {− 1 , +1 } 21 th September 2020 - 25 th September 2020 T.Stibor (GSI) ML for Beginners

Perceptron Learning Algorithm input : ( x 1 , y 1 ) , . . . , ( x N , y N ) ∈ R d +1 × {− 1 , +1 } , η ∈ R + , max.epoch ∈ N output: w begin Randomly initialize w ; epoch ← 0 ; repeat for i ← 1 to N do if y i � w , x i � ≤ 0 then w ← w + η x i y i epoch ← epoch + 1 until ( epoch = max.epoch ) or ( no change in w ); return w 21 th September 2020 - 25 th September 2020 T.Stibor (GSI) ML for Beginners

Training the Perceptron (cont.) Geometrical explanation: If x belongs to { +1 } and � w , x � < 0 ⇒ angle between x and w is greater than 90 ◦ , rotate w in direction of x to bring missclassified x into the positive half space defined by w . Same idea if x belongs to {− 1 } and � w , x � ≥ 0. +1 positive halfspace +1 positive halfspace w new w w x x − 1 negative halfspace − 1 negative halfspace 21 th September 2020 - 25 th September 2020 T.Stibor (GSI) ML for Beginners

Perceptron Error Reduction Recall: missclassifcation results in: w new = w + η x y , this reduces the error since 1 ( x y ) T ( x y ) − w T − w T ( x y ) − new ( x y ) = η ���� � �� � > 0 � x y � 2 > 0 − w T x y < How often one has to cycle through the patterns in the training set? A finite number of steps? 1 right multiply with − ( x y ) and transpose term before 21 th September 2020 - 25 th September 2020 T.Stibor (GSI) ML for Beginners

Perceptron Convergence Theorem Proposition Given a finite and linearly separable training set. The perceptron converges after some finite steps [Rosenblatt, 1962]. 21 th September 2020 - 25 th September 2020 T.Stibor (GSI) ML for Beginners

Perceptron Algorithm (R-code) ################################################### perceptron <- function(w,X,y,eta,max.epoch) { ################################################### N <- nrow(X); epoch <- 0; repeat { w.old <- w; for (i in 1:N) { if ( y[i] * (X[i,] %*% w) <= 0 ) w <- w + eta * y[i] * X[i,]; } epoch <- epoch + 1; if ( identical(w.old,w) || epoch = max.epoch ) { break; # terminate if no change in weights or max.epoch } } return (w); 21 th September 2020 - 25 th September 2020 } T.Stibor (GSI) ML for Beginners

Perceptron Algorithm Visualization 6 6 4 4 2 2 X[, 2:3][,2] X[, 2:3][,2] 0 0 −2 −2 −4 −4 −4 −2 0 2 4 6 −4 −2 0 2 4 6 X[, 2:3][,1] X[, 2:3][,1] One epoch terminate if no change in w 21 th September 2020 - 25 th September 2020 T.Stibor (GSI) ML for Beginners

Perceptron Algorithm Visualization 6 6 4 4 2 2 X[, 2:3][,2] X[, 2:3][,2] 0 0 −2 −2 −4 −4 −4 −2 0 2 4 6 −4 −2 0 2 4 6 X[, 2:3][,1] X[, 2:3][,1] One epoch terminate if no change in w 21 th September 2020 - 25 th September 2020 T.Stibor (GSI) ML for Beginners

From Perceptron Loss Θ to Gradient Descent The parameters to learn are: ( w 0 , w 1 , w 2 ) = w . What is our loss function Loss Θ we would like to minimize? Where is term w new = w + η x y coming from? � Loss Θ � = E ( w ) = − � w , x m � y m m ∈M where M denotes the set of all missclassified patterns. Moreover, Loss Θ is continuous and piecewise linear and fits in the spirit iterative gradient descent method w new = w + η ∇ E ( w ) = w + η x y 21 th September 2020 - 25 th September 2020 T.Stibor (GSI) ML for Beginners

Method of Gradient Descent Let E ( w ) be a continuously differentiable function of some unknown (weight) vector w . Find an optimal solution w ⋆ that satisfies the condition E ( w ⋆ ) ≤ E ( w ) . The necessary condition for optimality is ∇ E ( w ⋆ ) = 0 . Let us consider the following iterative descent: Start with an initial guess w (0) and generate sequence of weight vectors w (1) , w (2) , . . . such that E ( w ( i +1) ) ≤ E ( w ( i ) ) . 21 th September 2020 - 25 th September 2020 T.Stibor (GSI) ML for Beginners

Gradient Descent Algorithm w ( i +1) = w ( i ) − η ∇ E ( w ( i ) ) where η is a positive constant called learning rate. At each iteration step the algorithm applies the correction w ( i +1) − w ( i ) ∆ w ( i ) = − η ∇ E ( w ( i ) ) = Gradient descent algorithm satisfies: E ( w ( i +1) ) ≤ E ( w ( i ) ) , to see this, use first-order Taylor expansion around w ( i ) to approximate E ( w ( i +1) ) as E ( w ( i ) ) + ( ∇ E ( w ( i ) )) T ∆ w ( i ) . 21 th September 2020 - 25 th September 2020 T.Stibor (GSI) ML for Beginners